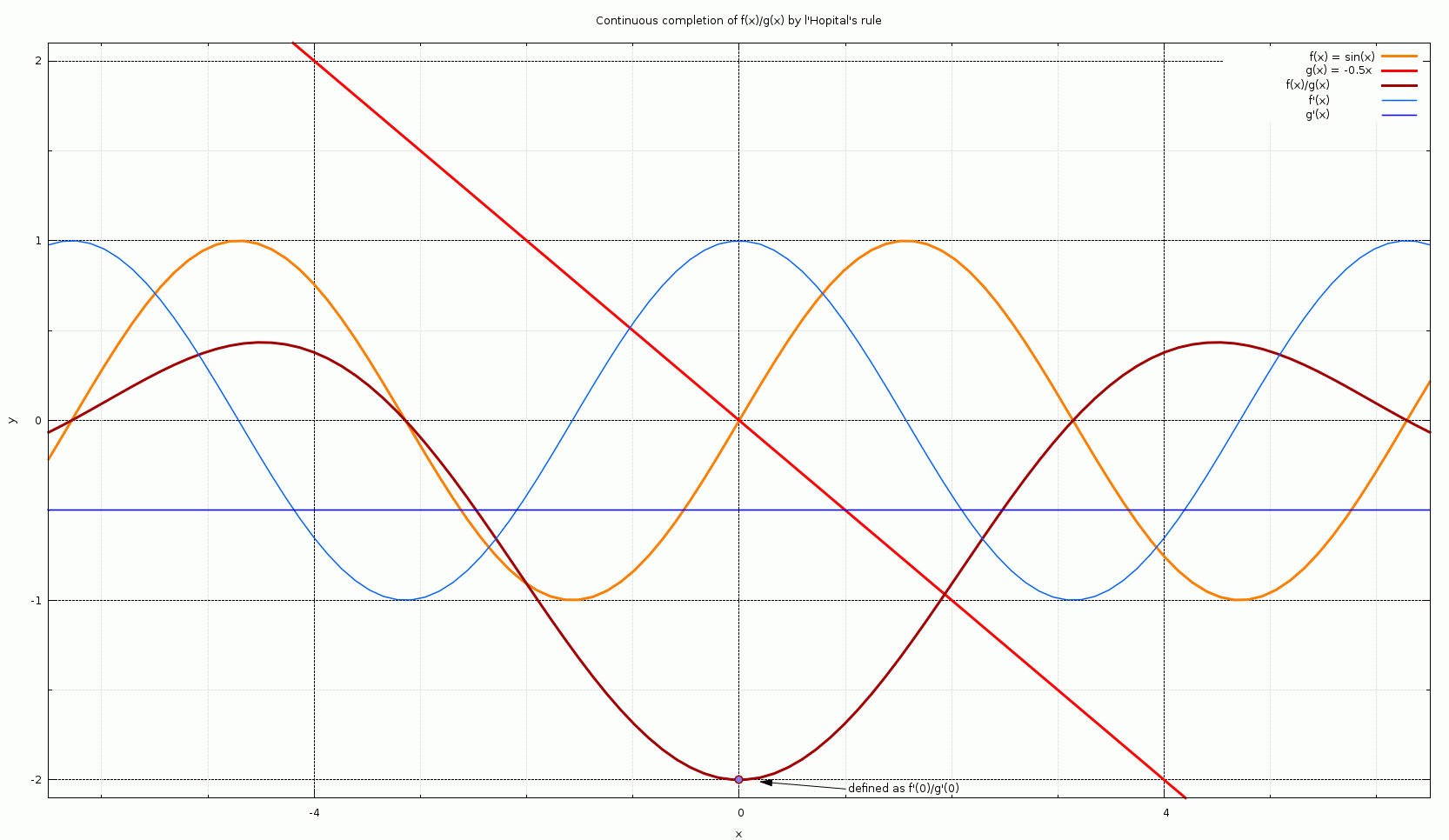
L'Hôpital's Rule

L'Hôpital's rule (, ), also known as Bernoulli's rule, is a mathematical theorem that allows evaluating limits of indeterminate forms using derivatives. Application (or repeated application) of the rule often converts an indeterminate form to an expression that can be easily evaluated by substitution. The rule is named after the 17th-century French mathematician Guillaume de l'Hôpital. Although the rule is often attributed to de l'Hôpital, the theorem was first introduced to him in 1694 by the Swiss mathematician Johann Bernoulli.

L'Hôpital's rule states that for functions and which are defined on an open interval and differentiable on $I\setminus \$ for a (possibly infinite) accumulation point of , if $\lim \limits_f(x)=\lim \limits_g(x)=0 \text\pm\infty,$ and $g'(x)\ne 0$ for all in $I\setminus \$, and $\lim \limits_\frac$ exists, then
:$\lim_\frac = \lim_\frac.$

The differentiation of the numerator and denominator often simplifies the quotient or converts it to a limit that can be directly evaluated by continuity.

History

Guillaume de l'Hôpital (also written l'Hospital) published this rule in his 1696 book '' Analyse des Infiniment Petits pour l'Intelligence des Lignes Courbes'' (literal translation: ''Analysis of the Infinitely Small for the Understanding of Curved Lines''), the first textbook on differential calculus. However, it is believed that the rule was discovered by the Swiss mathematician Johann Bernoulli.

General form

The general form of l'Hôpital's rule covers many cases. Let and be extended real numbers: real numbers, as well as positive and negative infinity. Let be an open interval containing (for a two-sided limit) or an open interval with endpoint (for a one-sided limit, or a limit at infinity if is infinite). On $I\smallsetminus \$, the real-valued functions and are assumed differentiable with $g'(x) \ne 0$. It is also assumed that $\lim \limits_ \frac = L$, a finite or infinite limit.

If either$\lim_f(x) = \lim_g(x) = 0$or$\lim_ , f(x), = \lim_ , g(x), = \infty,$then$\lim_ \frac = L.$Although we have written throughout, the limits may also be one-sided limits ( or ), when is a finite endpoint of .

In the second case, the hypothesis that diverges to infinity is not necessary; in fact, it is sufficient that $\lim_ , g(x), = \infty.$

The hypothesis that $g'(x)\ne 0$ appears most commonly in the literature, but some authors sidestep this hypothesis by adding other hypotheses which imply $g'(x)\ne 0$. For example, one may require in the definition of the limit $\lim \limits_ \frac = L$ that the function $\frac$ must be defined everywhere on an interval $I\smallsetminus \$. Another method is to require that both and be differentiable everywhere on an interval containing .

Necessity of conditions: Counterexamples

All four conditions for l'Hôpital's rule are necessary:

# Indeterminacy of form: $\lim_ f(x) = \lim_ g(x) = 0$ or $\pm \infty$ ;
# Differentiability of functions: $f(x)$ and $g(x)$ are differentiable on an open interval $\mathcal$ except possibly at the limit point $c$ in $\mathcal$;
# Non-zero derivative of denominator: $g'(x) \ne 0$ for all $x$ in $\mathcal$ with $x \ne c$ ;
# Existence of limit of the quotient of the derivatives: $\lim_ \frac$ exists.

Where one of the above conditions is not satisfied, l'Hôpital's rule is not valid in general, and its conclusion may be false in certain cases.

1. Form is not indeterminate

The necessity of the first condition can be seen by considering the counterexample where the functions are $f(x) = x +1$ and $g(x) = 2x +1$ and the limit is $x \to 1$.

The first condition is not satisfied for this counterexample because $\lim_ f(x) = \lim_ (x + 1) = (1) + 1 = 2 \neq 0$ and $\lim_ g(x) = \lim_ (2x + 1) = 2(1) + 1 = 3 \neq 0$. This means that the form is not indeterminate.

The second and third conditions are satisfied by $f(x)$ and $g(x)$. The fourth condition is also satisfied with

$\lim_ \frac = \lim_ \frac = \lim_ \frac = \frac.$

But the conclusion fails, since $\lim_ \frac = \lim_ \frac = \frac = \frac \neq \frac.$

2. Differentiability of functions

Differentiability of functions is a requirement because if a function is not differentiable, then the derivative of the function is not guaranteed to exist at each point in $\mathcal$. The fact that $\mathcal$ is an open interval is grandfathered in from the hypothesis of the Cauchy's mean value theorem. The notable exception of the possibility of the functions being not differentiable at $c$ exists because l'Hôpital's rule only requires the derivative to exist as the function approaches $c$; the derivative does not need to be taken at $c$.

For example, let $f(x) = \begin \sin x, & x\neq0 \\ 1, & x=0 \end$ , $g(x)=x$, and $c = 0$. In this case, $f(x)$ is not differentiable at $c$. However, since $f(x)$ is differentiable everywhere except $c$, then $\lim_f'(x)$ still exists. Thus, since

$\lim_ \frac = \frac$ and $\lim_ \frac$ exists, l'Hôpital's rule still holds.

3. Derivative of denominator is zero

The necessity of the condition that $g'(x)\ne 0$ near $c$ can be seen by the following counterexample due to Otto Stolz. Let $f(x)=x+\sin x \cos x$ and $g(x)=f(x)e^.$ Then there is no limit for $f(x)/g(x)$ as $x\to\infty.$ However,

:$\begin \frac &= \frac \\ &= \frac e^, \end$

which tends to 0 as $x\to\infty$, although it is undefined at infinitely many points. Further examples of this type were found by Ralph P. Boas Jr.

4. Limit of derivatives does not exist

The requirement that the limit $\lim_\frac$ exists is essential; if it does not exist, the original limit $\lim_\frac$ may nevertheless exist. Indeed, as $x$ approaches $c$, the functions $f$ or $g$ may exhibit many oscillations of small amplitude but steep slope, which do not affect $\lim_\frac$ but do prevent the convergence of $\lim_\frac$.

For example, if $f(x)=x+\sin(x)$, $g(x)=x$ and $c=\infty$, then $\frac=\frac,$which does not approach a limit since cosine oscillates infinitely between and . But the ratio of the original functions does approach a limit, since the amplitude of the oscillations of $f$ becomes small relative to $g$:

:$\lim_\frac = \lim_\left(\frac\right) = \lim_\left(1+\frac\right) = 1+0 = 1.$

In a case such as this, all that can be concluded is that

: $\liminf_ \frac \leq \liminf_ \frac \leq \limsup_ \frac \leq \limsup_ \frac ,$

so that if the limit of $\frac$ exists, then it must lie between the inferior and superior limits of $\frac$ . In the example, 1 does indeed lie between 0 and 2.)

Note also that by the contrapositive form of the Rule, if $\lim_\frac$ does not exist, then $\lim_\frac$ also does not exist.

Examples

In the following computations, we indicate each application of l'Hôpital's rule by the symbol $\ \stackrel\$.
* Here is a basic example involving the exponential function, which involves the indeterminate form at : $\lim_ \frac \ \stackrel\ \lim_ \frac = \lim_ \frac = 1.$
* This is a more elaborate example involving . Applying l'Hôpital's rule a single time still results in an indeterminate form. In this case, the limit may be evaluated by applying the rule three times:
\begin
\lim_
& \ \stackrel\ \lim_ \\ pt& \ \stackrel\ \lim_ \\ pt& \ \stackrel\ \lim_
= =6.
\end
* Here is an example involving : $\lim_x^n\cdot e^ =\lim_ \ \stackrel\ \lim_ =n\cdot \lim_.$ Repeatedly apply l'Hôpital's rule until the exponent is zero (if is an integer) or negative (if is fractional) to conclude that the limit is zero.
* Here is an example involving the indeterminate form (see below), which is rewritten as the form : $\lim_x \ln x =\lim_ \frac \ \stackrel\ \lim_ \frac = \lim_ -x = 0.$
*Here is an example involving the mortgage repayment formula and . Let be the principal (loan amount), the interest rate per period and the number of periods. When is zero, the repayment amount per period is $\frac$ (since only principal is being repaid); this is consistent with the formula for non-zero interest rates: $\lim_\frac \ \stackrel\ P \lim_ \frac = \frac.$
* One can also use l'Hôpital's rule to prove the following theorem. If is twice-differentiable in a neighborhood of and its second derivative is continuous on this neighborhood, then \begin
\lim_\frac
&= \lim_\frac \\ pt &= \lim_\frac \\ pt &= f''(x).
\end
*

Sometimes l'Hôpital's rule is invoked in a tricky way: suppose $f(x) + f'(x)$ converges as and that $e^x\cdot f(x)$ converges to positive or negative infinity. Then:$\lim_f(x) = \lim_\frac \ \stackrel\ \lim_\frac = \lim_\bigl(f(x)+f'(x)\bigr),$and so, $\lim_f(x)$ exists and $\lim_f'(x) = 0.$ (This result remains true without the added hypothesis that $e^x\cdot f(x)$ converges to positive or negative infinity, but the justification is then incomplete.)

Complications

Sometimes L'Hôpital's rule does not reduce to an obvious limit in a finite number of steps, unless some intermediate simplifications are applied. Examples include the following:

* Two applications can lead to a return to the original expression that was to be evaluated: $\lim_ \frac \ \stackrel\ \lim_ \frac \ \stackrel\ \lim_ \frac \ \stackrel\ \cdots .$ This situation can be dealt with by substituting $y=e^x$ and noting that goes to infinity as goes to infinity; with this substitution, this problem can be solved with a single application of the rule: $\lim_ \frac = \lim_ \frac \ \stackrel\ \lim_ \frac = \frac = 1.$ Alternatively, the numerator and denominator can both be multiplied by $e^x,$ at which point L'Hôpital's rule can immediately be applied successfully: $\lim_ \frac = \lim_ \frac \ \stackrel\ \lim_ \frac = 1.$
*An arbitrarily large number of applications may never lead to an answer even without repeating:$\lim_ \frac \ \stackrel\ \lim_ \frac \ \stackrel\ \lim_ \frac \ \stackrel\ \cdots .$This situation too can be dealt with by a transformation of variables, in this case $y = \sqrt$: $\lim_ \frac = \lim_ \frac \ \stackrel\ \lim_ \frac = \frac1 = 1.$ Again, an alternative approach is to multiply numerator and denominator by $x^$ before applying L'Hôpital's rule: $\lim_ \frac = \lim_ \frac \ \stackrel\ \lim_ \frac = 1.$

A common logical fallacy is to use L'Hôpital's rule to prove the value of a derivative by computing the limit of a difference quotient. Since applying l'Hôpital requires knowing the relevant derivatives, this amounts to circular reasoning or begging the question, assuming what is to be proved. For example, consider the proof of the derivative formula for powers of ''x'':

:$\lim_\frac=nx^.$

Applying L'Hôpital's rule and finding the derivatives with respect to yields
as expected, but this computation requires the use of the very formula that is being proven. Similarly, to prove $\lim_\frac=1$, applying L'Hôpital requires knowing the derivative of $\sin(x)$ at $x=0$, which amounts to calculating $\lim_\frac$ in the first place; a valid proof requires a different method such as the squeeze theorem.

Other indeterminate forms

Other indeterminate forms, such as , , , , and , can sometimes be evaluated using L'Hôpital's rule. We again indicate applications of L'Hopital's rule by $\ \stackrel\$.

For example, to evaluate a limit involving , convert the difference of two functions to a quotient:

:
\begin
\lim_\left(\frac-\frac1\right)
& = \lim_\frac \\ pt& \ \stackrel\ \lim_\frac \\ pt& = \lim_\frac \\ pt& \ \stackrel\ \lim_\frac = \frac.
\end

L'Hôpital's rule can be used on indeterminate forms involving exponents by using logarithms to "move the exponent down". Here is an example involving the indeterminate form :

:$\lim_x^x = \lim_e^ = \lim_e^ = \lim_\exp(x\cdot\ln x) = \exp().$

It is valid to move the limit inside the exponential function because this function is continuous. Now the exponent $x$ has been "moved down". The limit $\lim_x\cdot\ln x$ is of the indeterminate form dealt with in an example above: L'Hôpital may be used to determine that

:$\lim_x\cdot\ln x = 0.$

Thus

:$\lim_x^x =\exp(0) = e^0 = 1.$

The following table lists the most common indeterminate forms and the transformations which precede applying l'Hôpital's rule:

Stolz–Cesàro theorem

The Stolz–Cesàro theorem is a similar result involving limits of sequences, but it uses finite difference operators rather than derivatives.

Geometric interpretation: parametric curve and velocity vector

Consider the parametric curve in the ''xy''-plane with coordinates given by the continuous functions $g(t)$ and $f(t)$, the locus of points $(g(t),f(t))$, and suppose $f(c) = g(c) = 0$. The slope of the tangent to the curve at $(g(c),f(c))=(0,0)$ is the limit of the ratio $\textstyle \frac$ as . The tangent to the curve at the point $(g(t),f(t))$ is the velocity vector $(g'(t),f'(t))$ with slope $\textstyle \frac$. L'Hôpital's rule then states that the slope of the curve at the origin () is the limit of the tangent slope at points approaching the origin, provided that this is defined.

Proof of L'Hôpital's rule

Special case

The proof of L'Hôpital's rule is simple in the case where and are continuously differentiable at the point and where a finite limit is found after the first round of differentiation. This is only a special case of L'Hôpital's rule, because it only applies to functions satisfying stronger conditions than required by the general rule. However, many common functions have continuous derivatives (e.g. polynomials, sine and cosine, exponential functions), so this special case covers most applications.

Suppose that and are continuously differentiable at a real number , that $f(c)=g(c)=0$, and that $g'(c)\neq 0$. Then

:
\begin
& \lim_\frac = \lim_\frac = \lim_\frac \\ pt= & \lim_\frac = \frac= \frac = \lim_\frac.
\end

This follows from the difference quotient definition of the derivative. The last equality follows from the continuity of the derivatives at . The limit in the conclusion is not indeterminate because $g'(c)\ne 0$.

The proof of a more general version of L'Hôpital's rule is given below.

General proof

The following proof is due to , where a unified proof for the $\frac$ and $\frac$ indeterminate forms is given. Taylor notes that different proofs may be found in and .

Let ''f'' and ''g'' be functions satisfying the hypotheses in the General form section. Let $\mathcal$ be the open interval in the hypothesis with endpoint ''c''. Considering that $g'(x)\ne 0$ on this interval and ''g'' is continuous, $\mathcal$ can be chosen smaller so that ''g'' is nonzero on $\mathcal$.

For each ''x'' in the interval, define $m(x)=\inf\frac$ and $M(x)=\sup\frac$ as $t$ ranges over all values between ''x'' and ''c''. (The symbols inf and sup denote the infimum and supremum.)

From the differentiability of ''f'' and ''g'' on $\mathcal$, Cauchy's mean value theorem ensures that for any two distinct points ''x'' and ''y'' in $\mathcal$ there exists a $\xi$ between ''x'' and ''y'' such that $\frac=\frac$. Consequently, $m(x)\leq \frac \leq M(x)$ for all choices of distinct ''x'' and ''y'' in the interval. The value ''g''(''x'')-''g''(''y'') is always nonzero for distinct ''x'' and ''y'' in the interval, for if it was not, the mean value theorem would imply the existence of a ''p'' between ''x'' and ''y'' such that ''g' ''(''p'')=0.

The definition of ''m''(''x'') and ''M''(''x'') will result in an extended real number, and so it is possible for them to take on the values ±∞. In the following two cases, ''m''(''x'') and ''M''(''x'') will establish bounds on the ratio .

Case 1: $\lim_f(x)=\lim_g(x)=0$

For any ''x'' in the interval $\mathcal$, and point ''y'' between ''x'' and ''c'',
:$m(x)\le \frac=\frac\le M(x)$
and therefore as ''y'' approaches ''c'', $\frac$ and $\frac$ become zero, and so
:$m(x)\leq\frac\leq M(x).$

Case 2: $\lim_, g(x), =\infty$

For every ''x'' in the interval $\mathcal$, define $S_x=\$. For every point ''y'' between ''x'' and ''c'',
: $m(x)\le \frac=\frac \le M(x).$

As ''y'' approaches ''c'', both $\frac$ and $\frac$ become zero, and therefore
: $m(x)\le \liminf_ \frac \le \limsup_ \frac \le M(x).$

The limit superior and limit inferior are necessary since the existence of the limit of has not yet been established.

It is also the case that
:$\lim_m(x)=\lim_M(x)=\lim_\frac=L.$

and
:$\lim_\left(\liminf_\frac\right)=\liminf_\frac$ and $\lim_\left(\limsup_ \frac\right)=\limsup_\frac.$

In case 1, the squeeze theorem establishes that $\lim_\frac$ exists and is equal to ''L''. In the case 2, and the squeeze theorem again asserts that $\liminf_\frac=\limsup_\frac=L$, and so the limit $\lim_\frac$ exists and is equal to ''L''. This is the result that was to be proven.

In case 2 the assumption that ''f''(''x'') diverges to infinity was not used within the proof. This means that if , ''g''(''x''), diverges to infinity as ''x'' approaches ''c'' and both ''f'' and ''g'' satisfy the hypotheses of L'Hôpital's rule, then no additional assumption is needed about the limit of ''f''(''x''): It could even be the case that the limit of ''f''(''x'') does not exist. In this case, L'Hopital's theorem is actually a consequence of Cesàro–Stolz.

In the case when , ''g''(''x''), diverges to infinity as ''x'' approaches ''c'' and ''f''(''x'') converges to a finite limit at ''c'', then L'Hôpital's rule would be applicable, but not absolutely necessary, since basic limit calculus will show that the limit of ''f''(''x'')/''g''(''x'') as ''x'' approaches ''c'' must be zero.

Corollary

A simple but very useful consequence of L'Hopital's rule is that the derivative of a function cannot have a removable discontinuity. That is, suppose that ''f'' is continuous at ''a'', and that $f'(x)$ exists for all ''x'' in some open interval containing ''a'', except perhaps for $x = a$. Suppose, moreover, that $\lim_f'(x)$ exists. Then $f'(a)$ also exists and
:$f'(a) = \lim_f'(x).$
In particular, ''f is also continuous at ''a''.

Thus, if a function is not continuously differentiable near a point, the derivative must have an essential discontinuity at that point.

Proof

Consider the functions $h(x) = f(x)-f(a)$ and $g(x) = x-a$. The continuity of ''f'' at ''a'' tells us that $\lim_h(x) = 0$. Moreover, $\lim_g(x) = 0$ since a polynomial function is always continuous everywhere. Applying L'Hopital's rule shows that $f'(a) := \lim_\frac = \lim_\frac = \lim_f'(x)$.

See also

* L'Hôpital controversy

Notes

References

Sources

*
*
*
*
*

{{DEFAULTSORT:Lhopital's Rule
Articles containing proofs
Theorems in calculus
Theorems in real analysis
Limits (mathematics)