Kontsevich Integral on:
[Wikipedia]
[Google]
[Amazon]
In the mathematical theory of knots, the Kontsevich invariant, also known as the Kontsevich integral of an oriented framed link, is a universal Vassiliev invariant in the sense that any coefficient of the Kontsevich invariant is of a finite type, and conversely any finite type invariant can be presented as a linear combination of such coefficients. It was defined by
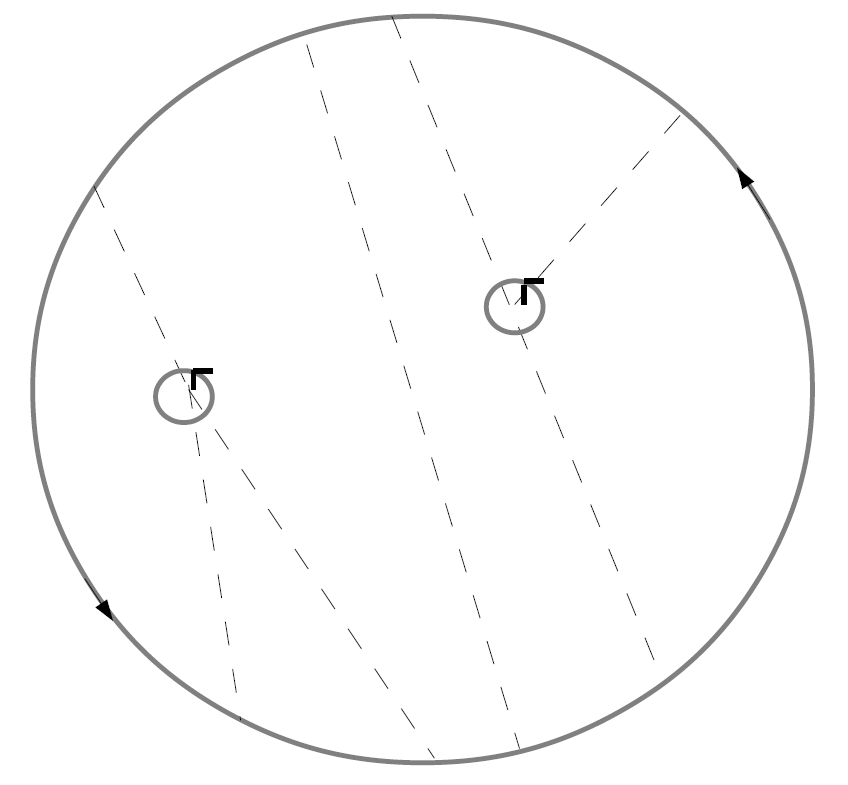 Let be a circle (which is a 1-dimensional manifold). As is shown in the figure on the right, a Jacobi diagram with order is the graph with vertices, with the external circle depicted as solid line circle and with dashed lines called inner graph, which satisfies the following conditions:
#The orientation is given only to the external circle.
#The vertices have values 1 or 3. The valued 3 vertices are connected to one of the other edge with clockwise or anti-clockwise direction depicted as the little directed circle. The valued 1 vertices are connected to the external circle without multiplicity, ordered by the orientation of the circle.
The edges on are called ''chords''. We denote as the quotient space of the commutative group generated by all the Jacobi diagrams on divided by the following relations:
:(The AS relation)
Let be a circle (which is a 1-dimensional manifold). As is shown in the figure on the right, a Jacobi diagram with order is the graph with vertices, with the external circle depicted as solid line circle and with dashed lines called inner graph, which satisfies the following conditions:
#The orientation is given only to the external circle.
#The vertices have values 1 or 3. The valued 3 vertices are connected to one of the other edge with clockwise or anti-clockwise direction depicted as the little directed circle. The valued 1 vertices are connected to the external circle without multiplicity, ordered by the orientation of the circle.
The edges on are called ''chords''. We denote as the quotient space of the commutative group generated by all the Jacobi diagrams on divided by the following relations:
:(The AS relation)  +
+  = 0
:(The IHX relation)
= 0
:(The IHX relation)  =
=  −
−  :(The STU relation)
:(The STU relation)  =
=  −
−  :(The FI relation)
:(The FI relation)  = 0.
A diagram without vertices valued 3 is called a chord diagram or Gauss diagram. If every connected component of a graph has a vertex valued 3, then we can make the Jacobi diagram into a Chord diagram using the STU relation recursively. If we restrict ourselves only to chord diagrams, then the above four relations are reduced to the following two relations:
:(The four term relation)
= 0.
A diagram without vertices valued 3 is called a chord diagram or Gauss diagram. If every connected component of a graph has a vertex valued 3, then we can make the Jacobi diagram into a Chord diagram using the STU relation recursively. If we restrict ourselves only to chord diagrams, then the above four relations are reduced to the following two relations:
:(The four term relation)  −
−  +
+  −
−  = 0.
:(The FI relation)
= 0.
:(The FI relation)  = 0.
= 0.
Maxim Kontsevich
Maxim Lvovich Kontsevich (russian: Макси́м Льво́вич Конце́вич, ; born 25 August 1964) is a Russian and French mathematician and mathematical physicist. He is a professor at the Institut des Hautes Études Scientifiques an ...
.
The Kontsevich invariant is a universal quantum invariant
In the mathematical field of knot theory, a quantum knot invariant or quantum invariant of a knot or link is a linear sum of colored Jones polynomial of surgery presentations of the knot complement.
List of invariants
*Finite type invariant
*Kont ...
in the sense that any quantum invariant may be recovered by substituting the appropriate weight system into any Jacobi diagram.
Definition
The Kontsevich invariant is defined bymonodromy
In mathematics, monodromy is the study of how objects from mathematical analysis, algebraic topology, algebraic geometry and differential geometry behave as they "run round" a singularity. As the name implies, the fundamental meaning of ''mono ...
along solutions of the Knizhnik–Zamolodchikov equations
In mathematical physics the Knizhnik–Zamolodchikov equations, or KZ equations, are linear differential equations satisfied by the correlation functions (on the Riemann sphere) of two-dimensional conformal field theories associated with an affine ...
.
Jacobi diagram and Chord diagram
Definition
 Let be a circle (which is a 1-dimensional manifold). As is shown in the figure on the right, a Jacobi diagram with order is the graph with vertices, with the external circle depicted as solid line circle and with dashed lines called inner graph, which satisfies the following conditions:
#The orientation is given only to the external circle.
#The vertices have values 1 or 3. The valued 3 vertices are connected to one of the other edge with clockwise or anti-clockwise direction depicted as the little directed circle. The valued 1 vertices are connected to the external circle without multiplicity, ordered by the orientation of the circle.
The edges on are called ''chords''. We denote as the quotient space of the commutative group generated by all the Jacobi diagrams on divided by the following relations:
:(The AS relation)
Let be a circle (which is a 1-dimensional manifold). As is shown in the figure on the right, a Jacobi diagram with order is the graph with vertices, with the external circle depicted as solid line circle and with dashed lines called inner graph, which satisfies the following conditions:
#The orientation is given only to the external circle.
#The vertices have values 1 or 3. The valued 3 vertices are connected to one of the other edge with clockwise or anti-clockwise direction depicted as the little directed circle. The valued 1 vertices are connected to the external circle without multiplicity, ordered by the orientation of the circle.
The edges on are called ''chords''. We denote as the quotient space of the commutative group generated by all the Jacobi diagrams on divided by the following relations:
:(The AS relation) Properties
* The degree of a Jacobi diagram is defined to be the half of the sum of the number of its vertices with value 1 and one with value 3. It is the number of chords in the Chord diagram transformed from the Jacobi diagram. * Just like for the tangles, the Jacobi diagrams form amonoidal category
In mathematics, a monoidal category (or tensor category) is a category \mathbf C equipped with a bifunctor
:\otimes : \mathbf \times \mathbf \to \mathbf
that is associative up to a natural isomorphism, and an object ''I'' that is both a left and r ...
with the composition as the compiling of Jacobi diagrams along up and down direction and the tensor product as juxtapositioning Jacobi diagrams.
** In the special case where is an interval , will be a commutative algebra. Viewing as the algebra with multiplication as connected sum
In mathematics, specifically in topology, the operation of connected sum is a geometric modification on manifolds. Its effect is to join two given manifolds together near a chosen point on each. This construction plays a key role in the classifi ...
s, is isomorphic to .
* A Jacobi diagram can be viewed as abstraction of representations of the tensor algebra generated by Lie algebras, which allows us to define some operations analogous to coproducts, counits and antipodes of Hopf algebra Hopf is a German surname. Notable people with the surname include:
*Eberhard Hopf (1902–1983), Austrian mathematician
*Hans Hopf (1916–1993), German tenor
*Heinz Hopf (1894–1971), German mathematician
*Heinz Hopf (actor) (1934–2001), Swedis ...
s.
* Since the Vassiliev invariant
Vasilyev, Vasiliev or Vassiliev or Vassiljev (russian: Васильев), or Vasilyeva or Vasilieva (feminine; russian: link=no, Васильева), is a common Russian surname that is derived from the Russian given name ''Vasiliy'' (equivalent o ...
s (or finite type invariants) are closely related to chord diagrams, one can construct a singular knot from a chord diagram on . denoting the space generated by all the singular knots with degree , every such determines a unique element in .
Weight system
A map from the Jacobi diagrams to the positive integers is called a ''weight system''. The map extended to the space is also called the weight system. They have the following properties: * Let be a semisimple Lie algebra and its representation. We obtain a weight system by "substituting" the invariant tensor of into the chord of a Jacobi diagram and into the underlying manifold of the Jacobi diagram. ** We can view the vertices with value 3 of the Jacobi diagram as the bracket product of the Lie algebra, solid line arrows as the representation space of , and the vertices with value 1 as the action of the Lie algebra. ** The IHX relation and the STU relation correspond respectively to the Jacobi identity and the definition of the representation ::: . * Weight systems play an essential role in the proof of the Mervin-Morton conjecture, which relatesAlexander polynomial
In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923. In 1969, John Conway showed a ve ...
s to Jones polynomial
In the mathematical field of knot theory, the Jones polynomial is a knot polynomial discovered by Vaughan Jones in 1984. Specifically, it is an invariant of an oriented knot or link which assigns to each oriented knot or link a Laurent polynom ...
s.
History
Jacobi diagrams were introduced as analogues of Feynman diagrams when Kontsevich defined knot invariants by iterated integrals in the first half of 1990s. He represented singular points of singular knots by chords, ''i.e.'' he treated only with chord diagrams. D. Bar-Natan later formulated them as the 1-3 valued graphs and studied their algebraic properties, and called them "Chinese character diagrams" in his paper. Several terms such as chord diagrams, web diagrams, or Feynman diagrams were used to refer them, but they have been called Jacobi diagrams since around 2000, because the IHX relation corresponds to the Jacobi identity forLie algebra
In mathematics, a Lie algebra (pronounced ) is a vector space \mathfrak g together with an Binary operation, operation called the Lie bracket, an Alternating multilinear map, alternating bilinear map \mathfrak g \times \mathfrak g \rightarrow ...
s.
We can interpret them from a more general point of view by claspers, which were defined independently by Goussarov and Kazuo Habiro in the later half of the 1990s.
References
Bibliography
* {{Cite book , publisher = World Scientific Publishing Company , isbn = 9789810246754 , ol = 9195378M , title = Quantum Invariants – A Study of Knots, 3-Manifolds, and their Sets , author = Ohtsuki, Tomotada , date = 2001 , edition=1st Knot invariants