inversely correlated

In mathematics, two sequences of numbers, often experimental data, are proportional or directly proportional if their corresponding elements have a constant ratio, which is called the coefficient of proportionality or proportionality constant. Two sequences are inversely proportional if corresponding elements have a constant product, also called the coefficient of proportionality.

This definition is commonly extended to related varying quantities, which are often called ''variables''. This meaning of ''variable'' is not the common meaning of the term in mathematics (see variable (mathematics)); these two different concepts share the same name for historical reasons.

Two functions $f(x)$ and $g(x)$ are ''proportional'' if their ratio $\frac$ is a constant function.

If several pairs of variables share the same direct proportionality constant, the equation expressing the equality of these ratios is called a proportion, e.g., (for details see Ratio).
Proportionality is closely related to ''linearity''.

Direct proportionality

Given two variables ''x'' and ''y'', ''y'' is directly proportional to ''x'' if there is a non-zero constant ''k'' such that

: $y = kx.$

The relation is often denoted using the symbols "∝" (not to be confused with the Greek letter alpha) or "~":
: $y \propto x,$ or $y \sim x.$

For $x \ne 0$ the proportionality constant can be expressed as the ratio

: $k = \frac.$

It is also called the constant of variation or constant of proportionality.

A direct proportionality can also be viewed as a linear equation in two variables with a ''y''-intercept of and a slope of ''k''. This corresponds to linear growth.

Examples

* If an object travels at a constant speed, then the distance traveled is directly proportional to the time spent traveling, with the speed being the constant of proportionality.
* The circumference of a circle is directly proportional to its diameter, with the constant of proportionality equal to .
* On a map of a sufficiently small geographical area, drawn to scale distances, the distance between any two points on the map is directly proportional to the beeline distance between the two locations represented by those points; the constant of proportionality is the scale of the map.
* The force, acting on a small object with small mass by a nearby large extended mass due to gravity, is directly proportional to the object's mass; the constant of proportionality between the force and the mass is known as gravitational acceleration.
* The net force acting on an object is proportional to the acceleration of that object with respect to an inertial frame of reference. The constant of proportionality in this, Newton's second law, is the classical mass of the object.

Computer encoding

Inverse proportionality

The concept of ''inverse proportionality'' can be contrasted with ''direct proportionality''. Consider two variables said to be "inversely proportional" to each other. If all other variables are held constant, the magnitude or absolute value of one inversely proportional variable decreases if the other variable increases, while their product (the constant of proportionality ''k'') is always the same. As an example, the time taken for a journey is inversely proportional to the speed of travel.

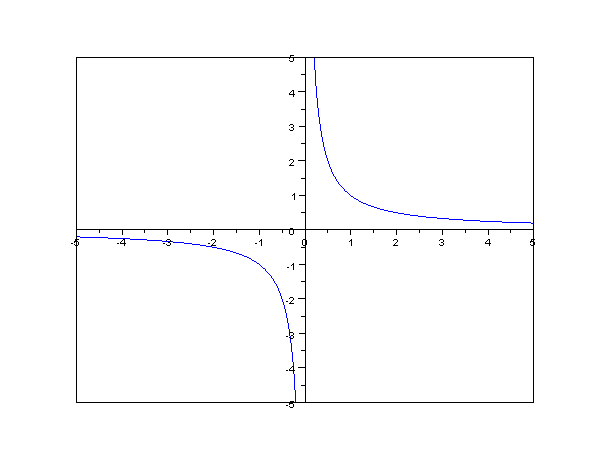
Formally, two variables are inversely proportional (also called varying inversely, in inverse variation, in inverse proportion) if each of the variables is directly proportional to the multiplicative inverse (reciprocal) of the other, or equivalently if their product is a constant.Weisstein, Eric W
"Inversely Proportional"
''MathWorld'' – A Wolfram Web Resource. It follows that the variable ''y'' is inversely proportional to the variable ''x'' if there exists a non-zero constant ''k'' such that
: $y = \frac,$
or equivalently, $xy = k.$ Hence the constant "''k''" is the product of ''x'' and ''y''.

The graph of two variables varying inversely on the Cartesian coordinate plane is a rectangular hyperbola. The product of the ''x'' and ''y'' values of each point on the curve equals the constant of proportionality (''k''). Since neither ''x'' nor ''y'' can equal zero (because ''k'' is non-zero), the graph never crosses either axis.

Hyperbolic coordinates

The concepts of ''direct'' and ''inverse'' proportion lead to the location of points in the Cartesian plane by hyperbolic coordinates; the two coordinates correspond to the constant of direct proportionality that specifies a point as being on a particular ray and the constant of inverse proportionality that specifies a point as being on a particular hyperbola.

See also

* Linear map
* Correlation
* Eudoxus of Cnidus
* Golden ratio
* Inverse-square law
* Proportional font
* Ratio
* Rule of three (mathematics)
* Sample size
* Similarity
* Basic proportionality theorem
* ∷ the ''a'' is to ''b'' as ''c'' is to ''d'' symbol (U+2237 ''PROPORTION'')

Growth

* Linear growth
* Hyperbolic growth

Notes

References

* Ya. B. Zeldovich, I. M. Yaglom: ''Higher math for beginners''
p. 34–35

* Brian Burrell: ''Merriam-Webster's Guide to Everyday Math: A Home and Business Reference''. Merriam-Webster, 1998,
p. 85–101

* Lanius, Cynthia S.; Williams Susan E.
''PROPORTIONALITY: A Unifying Theme for the Middle Grades''
Mathematics Teaching in the Middle School 8.8 (2003), p. 392–396.
* Seeley, Cathy; Schielack Jane F.
''A Look at the Development of Ratios, Rates, and Proportionality''
Mathematics Teaching in the Middle School, 13.3, 2007, p. 140–142.
* Van Dooren, Wim; De Bock Dirk; Evers Marleen; Verschaffel Lieven
''Students' Overuse of Proportionality on Missing-Value Problems: How Numbers May Change Solutions''
Journal for Research in Mathematics Education, 40.2, 2009, p. 187–211.

{{DEFAULTSORT:Proportionality (Mathematics)
Mathematical terminology
Ratios