Interval Scheduling on:
[Wikipedia]
[Google]
[Amazon]
Interval scheduling is a class of problems in
// The vectors are already sorted from earliest to latest finish time.
int v umOfVectors + 1 // list of interval vectors
int w umOfVectors + 1 // w is the weight for v
int p umOfVectors + 1 // p is the # of vectors that end before v begins.
int M umOfVectors + 1
int finalSchedule[];
// v[0] does not exist, and the first interval vector is assigned to v[1].
w[0] = 0; p[0] = 0; M[0] = 0;
// The following code determines the value of M for each vector.
// The maximum weight of the schedule is equal to M umOfVectors
for (int i = 1; i < numOfVectors + 1; i++)
// Function to construct the optimal schedule
schedule (j)
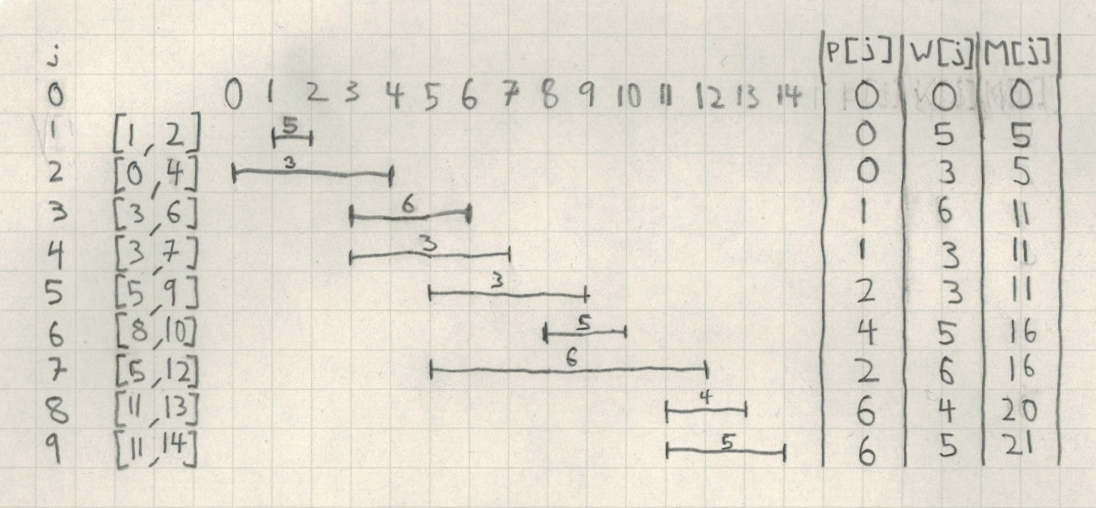 Here, we input our final vector (where j=9 in this example) into our schedule function from the code block above. We perform the actions in the table below until j is set to 0, at which point, we only include into our final schedule the encountered intervals which met the
Here, we input our final vector (where j=9 in this example) into our schedule function from the code block above. We perform the actions in the table below until j is set to 0, at which point, we only include into our final schedule the encountered intervals which met the
computer science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ...
, particularly in the area of algorithm
In mathematics and computer science, an algorithm () is a finite sequence of Rigour#Mathematics, mathematically rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algo ...
design. The problems consider a set of tasks. Each task is represented by an ''interval'' describing the time in which it needs to be processed by some machine (or, equivalently, scheduled on some resource). For instance, task A might run from 2:00 to 5:00, task B might run from 4:00 to 10:00 and task C might run from 9:00 to 11:00. A subset of intervals is ''compatible'' if no two intervals overlap on the machine/resource. For example, the subset is compatible, as is the subset ; but neither nor are compatible subsets, because the corresponding intervals within each subset overlap.
The ''interval scheduling maximization problem'' (ISMP) is to find a largest compatible set, i.e., a set of non-overlapping intervals of maximum size. The goal here is to execute as many tasks as possible, that is, to maximize the throughput
Network throughput (or just throughput, when in context) refers to the rate of message delivery over a communication channel in a communication network, such as Ethernet or packet radio. The data that these messages contain may be delivered ov ...
. It is equivalent to finding a maximum independent set
In mathematical analysis, the maximum and minimum of a function are, respectively, the greatest and least value taken by the function. Known generically as extremum, they may be defined either within a given range (the ''local'' or ''relative ...
in an interval graph
In graph theory, an interval graph is an undirected graph formed from a set of intervals on the real line,
with a vertex for each interval and an edge between vertices whose intervals intersect. It is the intersection graph of the intervals.
In ...
.
A generalization of the problem considers machines/resources. Here the goal is to find compatible subsets whose union is the largest.
In an upgraded version of the problem, the intervals are partitioned into groups. A subset of intervals is ''compatible'' if no two intervals overlap, and moreover, no two intervals belong to the same group (i.e., the subset contains at most a single representative of each group). Each group of intervals corresponds to a single task, and represents several alternative intervals in which it can be executed.
The ''group interval scheduling decision problem'' (GISDP) is to decide whether there exists a compatible set in which all groups are represented. The goal here is to execute a single representative task from each group. GISDPk is a restricted version of GISDP in which the number of intervals in each group is at most ''k''.
The ''group interval scheduling maximization problem'' (GISMP) is to find a largest compatible set - a set of non-overlapping representatives of maximum size. The goal here is to execute a representative task from as many groups as possible. GISMPk is a restricted version of GISMP in which the number of intervals in each group is at most ''k''. This problem is often called JISPk, where J stands for Job
Work, labor (labour in Commonwealth English), occupation or job is the intentional activity people perform to support the needs and desires of themselves, other people, or organizations. In the context of economics, work can be seen as the huma ...
.
GISMP is the most general problem; the other two problems can be seen as special cases of it:
* ISMP is the special case in which each task belongs to its own group (i.e. it is equal to GISMP1).
* GISDP is the problem of deciding whether the maximum exactly equals the number of groups.
All these problems can be generalized by adding a ''weight'' for each interval, representing the profit from executing the task in that interval. Then, the goal is to maximize the total weight.
All these problems are special cases of single-machine scheduling Single-machine scheduling or single-resource scheduling is an optimization problem in computer science and operations research. We are given ''n'' jobs ''J''1, ''J''2, ..., ''Jn'' of varying processing times, which need to be scheduled on a single m ...
, since they assume that all tasks must run on a single processor. Single-machine scheduling is a special case of optimal job scheduling
Optimal job scheduling is a class of optimization problems related to scheduling. The inputs to such problems are a list of '' jobs'' (also called ''processes'' or ''tasks'') and a list of ''machines'' (also called ''processors'' or ''workers''). T ...
.
Single-Interval Scheduling Maximization
Single-interval scheduling refers to creating an interval schedule in which no intervals overlap.Unweighted
Several algorithms, that may look promising at first sight, actually do not find the optimal solution: * Selecting the intervals that start earliest is not an optimal solution, because if the earliest interval happens to be very long, accepting it would make us reject many other shorter requests. * Selecting the shortest intervals or selecting intervals with the fewest conflicts is also not optimal. The followinggreedy algorithm
A greedy algorithm is any algorithm that follows the problem-solving heuristic of making the locally optimal choice at each stage. In many problems, a greedy strategy does not produce an optimal solution, but a greedy heuristic can yield locally ...
, called Earliest deadline first scheduling
Earliest deadline first (EDF) or least time to go is a dynamic priority scheduling algorithm used in real-time operating systems to place processes in a priority queue. Whenever a scheduling event occurs (task finishes, new task released, etc.) th ...
, does find the optimal solution for unweighted single-interval scheduling:
# Select the interval, ''x'', with the earliest finishing time.
# Remove ''x'', and all intervals intersecting ''x'', from the set of candidate intervals.
# Repeat until the set of candidate intervals is empty.
Whenever we select an interval at step 1, we may have to remove many intervals in step 2. However, all these intervals necessarily cross the finishing time of ''x'', and thus they all cross each other. Hence, at most 1 of these intervals can be in the optimal solution. Hence, for every interval in the optimal solution, there is an interval in the greedy solution. This proves that the greedy algorithm indeed finds an optimal solution.
A more formal explanation is given by a Charging argument.
The greedy algorithm can be executed in time O(''n'' log ''n''), where ''n'' is the number of tasks, using a preprocessing step in which the tasks are sorted by their finishing times.
Weighted
Problems involving weighted interval scheduling are equivalent to finding a maximum-weight independent set in aninterval graph
In graph theory, an interval graph is an undirected graph formed from a set of intervals on the real line,
with a vertex for each interval and an edge between vertices whose intervals intersect. It is the intersection graph of the intervals.
In ...
. Such problems can be solved in polynomial time.
Assuming the vectors are sorted from earliest to latest finish time, the following pseudocode determines the maximum weight of a single-interval schedule in Θ(n) time:Example
If we have the following 9 vectors sorted by finish time, with the weights above each corresponding interval, we can determine which of these vectors are included in our maximum weight schedule which only contains a subset of the following vectors. Here, we input our final vector (where j=9 in this example) into our schedule function from the code block above. We perform the actions in the table below until j is set to 0, at which point, we only include into our final schedule the encountered intervals which met the
Here, we input our final vector (where j=9 in this example) into our schedule function from the code block above. We perform the actions in the table below until j is set to 0, at which point, we only include into our final schedule the encountered intervals which met the