Hinged Dissection on:
[Wikipedia]
[Google]
[Amazon]
 In
In

 The concept of hinged dissections was popularised by the author of
The concept of hinged dissections was popularised by the author of
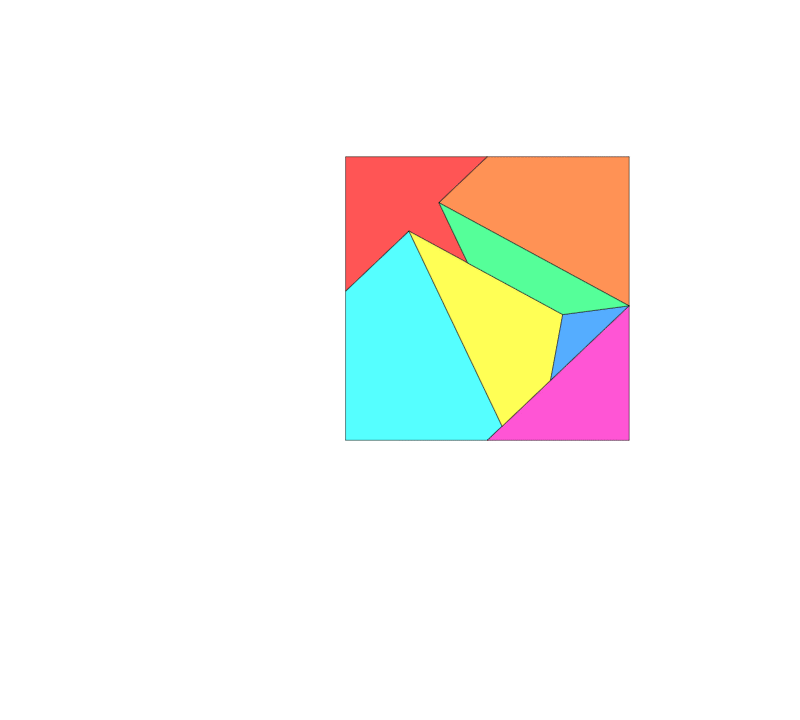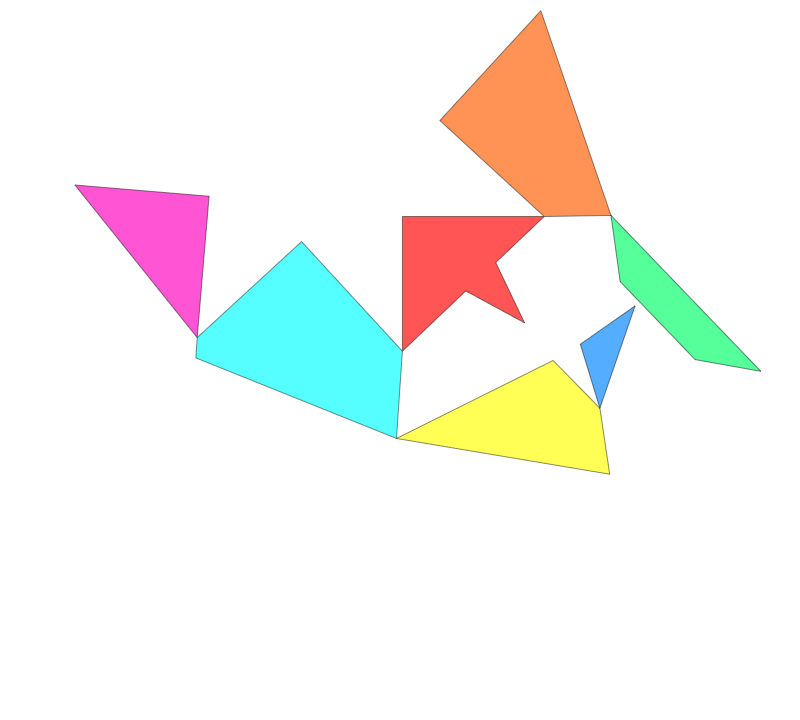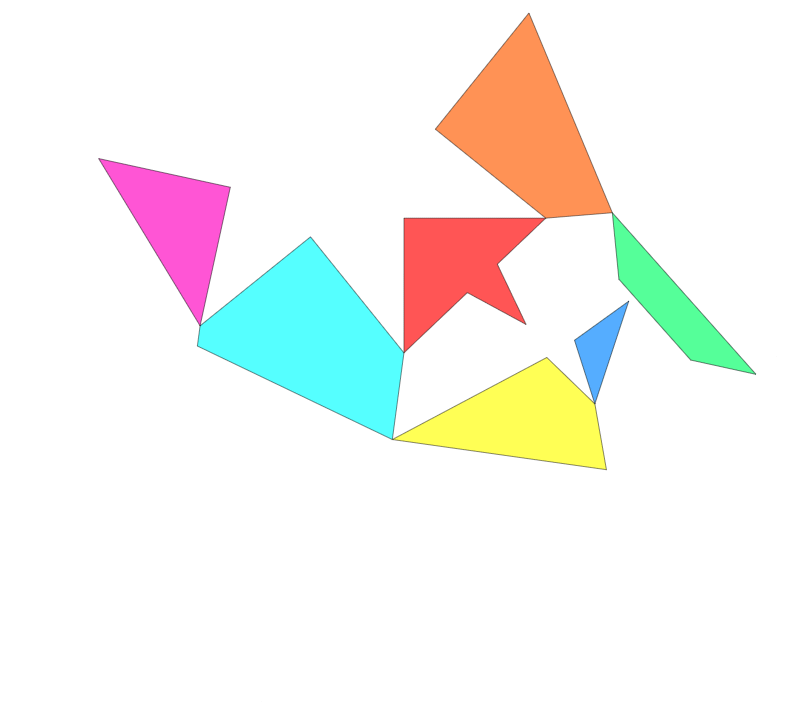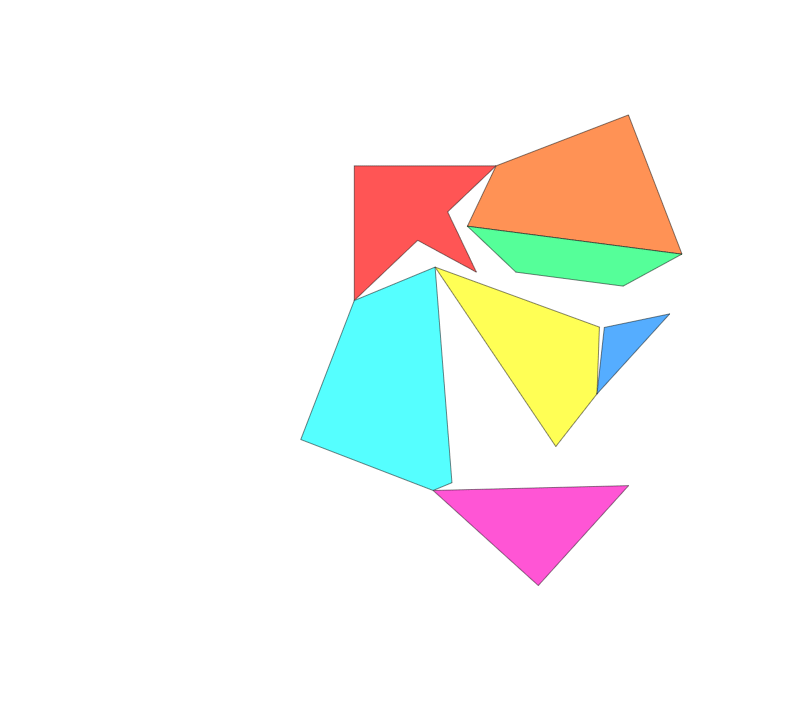 Other types of "hinges" have been considered in the context of dissections. A twist-hinge dissection is one which use a three-dimensional "hinge" which is placed on the edges of pieces rather than their vertices, allowing them to be "flipped" three-dimensionally.Frederickson 2002, p.6 As of 2002, the question of whether any two polygons must have a common twist-hinged dissection remains unsolved.Frederickson 2002, p. 7
Other types of "hinges" have been considered in the context of dissections. A twist-hinge dissection is one which use a three-dimensional "hinge" which is placed on the edges of pieces rather than their vertices, allowing them to be "flipped" three-dimensionally.Frederickson 2002, p.6 As of 2002, the question of whether any two polygons must have a common twist-hinged dissection remains unsolved.Frederickson 2002, p. 7
An applet demonstrating Dudeney's hinged square-triangle dissection
Geometric dissection Recreational mathematics Discrete geometry Euclidean plane geometry
 In
In geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
, a hinged dissection, also known as a swing-hinged dissection or Dudeney dissection, is a kind of geometric dissection
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
in which all of the pieces are connected into a chain by "hinged" points, such that the rearrangement from one figure
Figure may refer to:
General
*A shape, drawing, depiction, or geometric configuration
*Figure (wood), wood appearance
*Figure (music), distinguished from musical motif
* Noise figure, in telecommunication
* Dance figure, an elementary dance patt ...
to another can be carried out by swinging the chain continuously, without severing any of the connections. Typically, it is assumed that the pieces are allowed to overlap in the folding and unfolding process; this is sometimes called the "wobbly-hinged" model of hinged dissection.
History
 The concept of hinged dissections was popularised by the author of
The concept of hinged dissections was popularised by the author of mathematical puzzle
Mathematical puzzles make up an integral part of recreational mathematics. They have specific rules, but they do not usually involve competition between two or more players. Instead, to solve such a puzzle, the solver must find a solution that sati ...
s, Henry Dudeney
Henry Ernest Dudeney (10 April 1857 – 23 April 1930) was an English author and mathematician who specialised in logic puzzles and mathematical games. He is known as one of the foremost creators of mathematical puzzles.
Early life
Dudene ...
. He introduced the famous hinged dissection of a square into a triangle (pictured) in his 1907 book The Canterbury Puzzles.Frederickson 2002, p.1 The Wallace–Bolyai–Gerwien theorem
In geometry, the Wallace–Bolyai–Gerwien theorem, named after William Wallace (mathematician), William Wallace, Farkas Bolyai and P. Gerwien, is a theorem related to Dissection problem, dissections of polygons. It answers the question when one ...
, first proven in 1807, states that any two equal-area polygons must have a common dissection. However, the question of whether two such polygons must also share a ''hinged'' dissection remained open until 2007, when Erik Demaine
Erik D. Demaine (born February 28, 1981) is a Canadian-American professor of computer science at the Massachusetts Institute of Technology and a former child prodigy.
Early life and education
Demaine was born in Halifax, Nova Scotia, to mathe ...
''et al.'' proved that there must always exist such a hinged dissection, and provided a constructive algorithm to produce them. This proof holds even under the assumption that the pieces may not overlap while swinging, and can be generalised to any pair of three-dimensional figures which have a common dissection (see Hilbert's third problem
The third of Hilbert's problems, Hilbert's list of mathematical problems, presented in 1900, was the first to be solved. The problem is related to the following question: given any two polyhedron, polyhedra of equal volume, is it always possible t ...
). In three dimensions, however, the pieces are not guaranteed to swing without overlap.
Other hinges
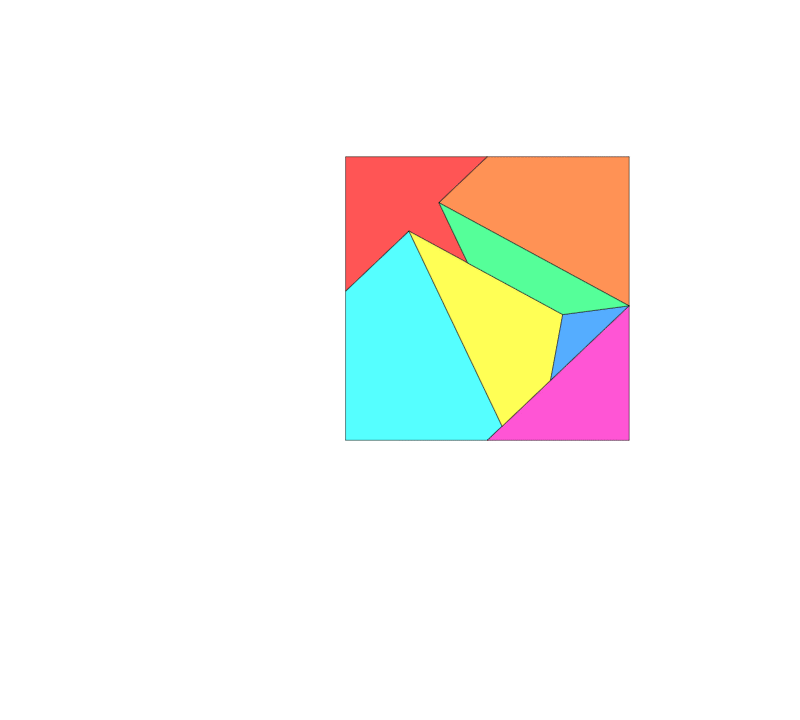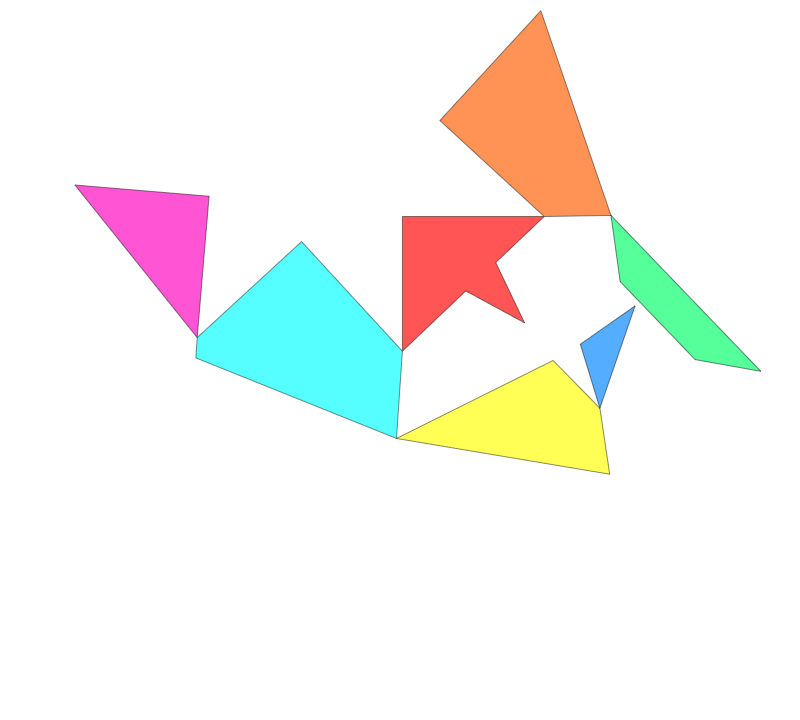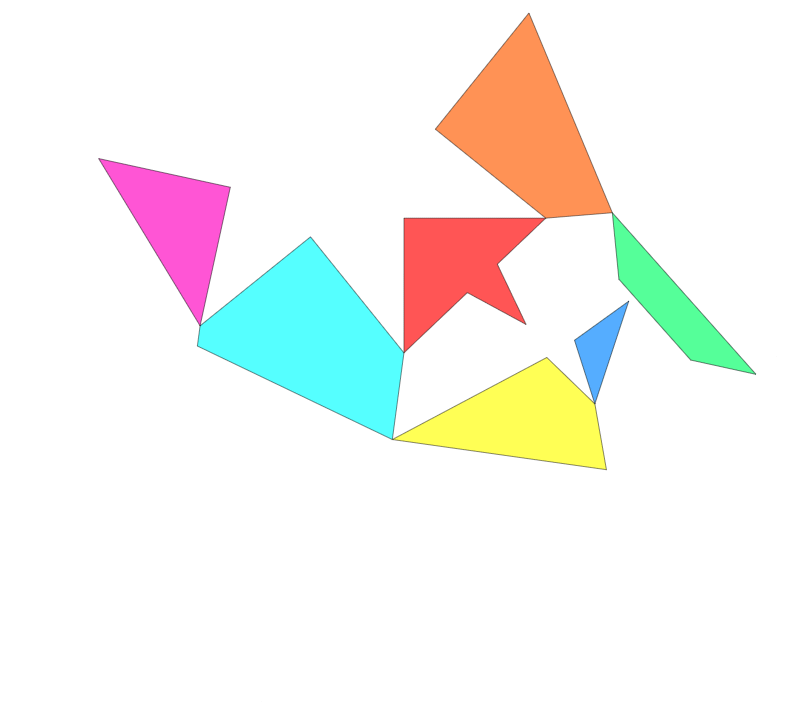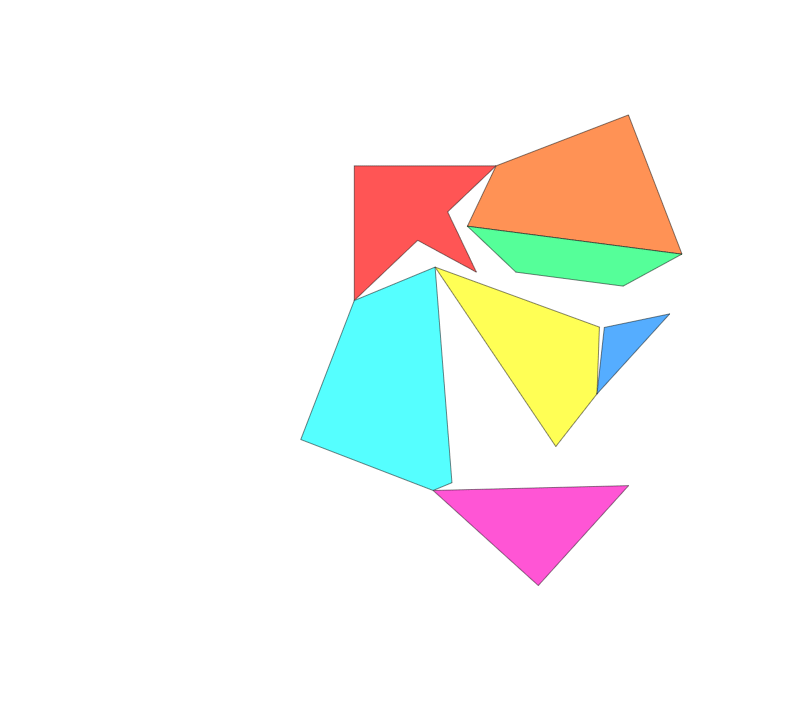 Other types of "hinges" have been considered in the context of dissections. A twist-hinge dissection is one which use a three-dimensional "hinge" which is placed on the edges of pieces rather than their vertices, allowing them to be "flipped" three-dimensionally.Frederickson 2002, p.6 As of 2002, the question of whether any two polygons must have a common twist-hinged dissection remains unsolved.Frederickson 2002, p. 7
Other types of "hinges" have been considered in the context of dissections. A twist-hinge dissection is one which use a three-dimensional "hinge" which is placed on the edges of pieces rather than their vertices, allowing them to be "flipped" three-dimensionally.Frederickson 2002, p.6 As of 2002, the question of whether any two polygons must have a common twist-hinged dissection remains unsolved.Frederickson 2002, p. 7
References
Bibliography
*{{cite book , last=Frederickson , first=Greg N. , date=26 August 2002 , title=Hinged Dissections: Swinging and Twisting , url=https://archive.org/details/hingeddissection0000fred , url-access=registration , publisher=Cambridge University Press , isbn=978-0521811927 , access-date=19 December 2013External links
An applet demonstrating Dudeney's hinged square-triangle dissection
Geometric dissection Recreational mathematics Discrete geometry Euclidean plane geometry