Horseshoe Orbit

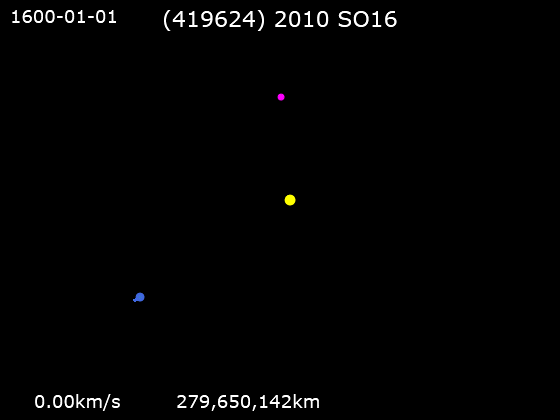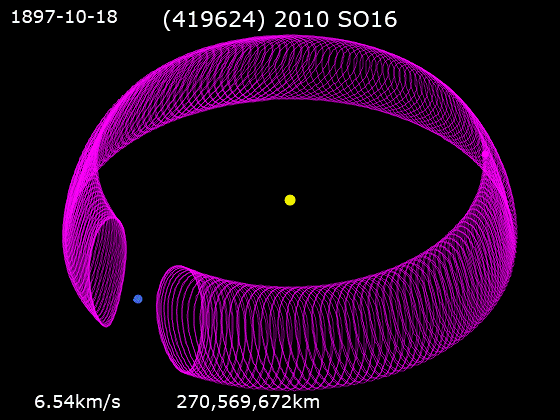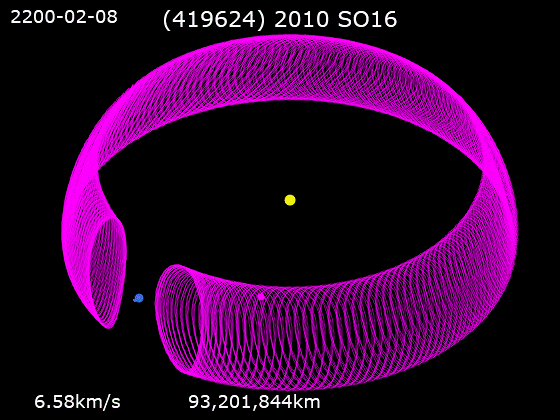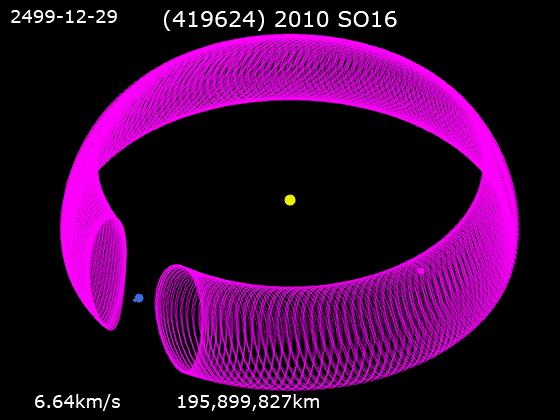In celestial mechanics, a horseshoe orbit is a type of co-orbital motion of a small orbiting body relative to a larger orbiting body. The osculating (instantaneous) orbital period of the smaller body remains very near that of the larger body, and if its orbit is a little more eccentric than that of the larger body, during every period it appears to trace an ellipse around a point on the larger object's orbit.
However, the loop is not closed but drifts forward or backward so that the point it circles will appear to move smoothly along the larger body's orbit over a long period of time. When the object approaches the larger body closely at either end of its trajectory, its apparent direction changes. Over an entire cycle the center traces the outline of a horseshoe, with the larger body between the 'horns'.

Asteroids in horseshoe orbits with respect to Earth include 54509 YORP, , , and possibly . A broader definition includes 3753 Cruithne, which can be said to be in a compound and/or transition orbit, or and . By 2016, 12 horseshoe librators of Earth have been discovered.

Saturn's moons Epimetheus and Janus occupy horseshoe orbits with respect to each other (in their case, there is no repeated looping: each one traces a full horseshoe with respect to the other).

Explanation of horseshoe orbital cycle

Background

The following explanation relates to an asteroid which is in such an orbit around the Sun, and is also affected by the Earth.

The asteroid is in almost the same solar orbit as Earth. Both take approximately one year to orbit the Sun.

It is also necessary to grasp two rules of orbit dynamics:

#A body closer to the Sun completes an orbit more quickly than a body farther away.
#If a body accelerates along its orbit, its orbit moves outwards from the Sun. If it decelerates, the orbital radius decreases.

The horseshoe orbit arises because the gravitational attraction of the Earth changes the shape of the elliptical orbit of the asteroid. The shape changes are very small but result in significant changes relative to the Earth.

The horseshoe becomes apparent only when mapping the movement of the asteroid relative to both the Sun and the Earth. The asteroid always orbits the Sun in the same direction. However, it goes through a cycle of catching up with the Earth and falling behind, so that its movement relative to both the Sun and the Earth traces a shape like the outline of a horseshoe.

Stages of the orbit

Starting at point A, on the inner ring between and Earth, the satellite is orbiting faster than the Earth and is on its way toward passing between the Earth and the Sun. But Earth's gravity exerts an outward accelerating force, pulling the satellite into a higher orbit which (per Kepler's third law) decreases its angular speed.

When the satellite gets to point B, it is traveling at the same speed as Earth. Earth's gravity is still accelerating the satellite along the orbital path, and continues to pull the satellite into a higher orbit. Eventually, at Point C, the satellite reaches a high and slow enough orbit such that it starts to lag behind Earth. It then spends the next century or more appearing to drift 'backwards' around the orbit when viewed relative to the Earth. Its orbit around the Sun still takes only slightly more than one Earth year. Given enough time, the Earth and the satellite will be on opposite sides of the Sun.

Eventually the satellite comes around to point D where Earth's gravity is now reducing the satellite's orbital velocity. This causes it to fall into a lower orbit, which actually increases the angular speed of the satellite around the Sun. This continues until point E where the satellite's orbit is now lower and faster than Earth's orbit, and it begins moving out ahead of Earth. Over the next few centuries it completes its journey back to point A.

On the longer term, asteroids can transfer between horseshoe orbits and quasi-satellite orbits. Quasi-satellites aren't gravitationally bound to their planet, but appear to circle it in a retrograde direction as they circle the Sun with the same orbital period as the planet. By 2016, orbital calculations showed that four of Earth's horseshoe librators and all five of its then known quasi-satellites repeatedly transfer between horseshoe and quasi-satellite orbits.

Energy viewpoint

A somewhat different, but equivalent, view of the situation may be noted by considering conservation of energy. It is a theorem of classical mechanics that a body moving in a time-independent potential field will have its total energy, ''E = T + V'', conserved, where ''E'' is total energy, ''T'' is kinetic energy (always non-negative) and ''V'' is potential energy, which is negative. It is apparent then, since ''V = -GM/R'' near a gravitating body of mass ''M'' and orbital radius ''R'', that seen from a ''stationary'' frame, V will be increasing for the region behind M, and decreasing for the region in front of it. However, orbits with lower total energy have shorter periods, and so a body moving slowly on the forward side of a planet will lose energy, fall into a shorter-period orbit, and thus slowly move away, or be "repelled" from it. Bodies moving slowly on the trailing side of the planet will gain energy, rise to a higher, slower, orbit, and thereby fall behind, similarly repelled. Thus a small body can move back and forth between a leading and a trailing position, never approaching too close to the planet that dominates the region.

Tadpole orbit

:''See also Trojan (celestial body).''
Figure 1 above shows shorter orbits around the Lagrangian points and (e.g. the lines close to the blue triangles). These are called tadpole orbits and can be explained in a similar way, except that the asteroid's distance from the Earth does not oscillate as far as the point on the other side of the Sun. As it moves closer to or farther from the Earth, the changing pull of Earth's gravitational field causes it to accelerate or decelerate, causing a change in its orbit known as libration.

An example of a tadpole orbit is Polydeuces, a small moon of Saturn which librates around the trailing point relative to a larger moon, Dione. In relation to the orbit of Earth, the asteroid is in a tadpole orbit around the leading point.
2020 VT1 follows a temporary horseshoe orbit with respect to Mars.

See also

* Box orbit
* Co-orbital moon
* Halo orbit
* Interplanetary Transport Network
* Lissajous orbit
* Natural satellite
* Quasi-satellite
* Temporary satellite

References

External links

Research paper describing Horseshoe orbits.
Start at page 105.

{{DEFAULTSORT:Horseshoe Orbit
Co-orbital objects
Three-body orbits
Orbits