Horizontal and vertical on:
[Wikipedia]
[Google]
[Amazon]
In

 In physics, engineering and construction, the direction designated as vertical is usually that along which a
In physics, engineering and construction, the direction designated as vertical is usually that along which a
 When the curvature of the earth is taken into account, the concepts of vertical and horizontal take on yet another meaning. On the surface of a smoothly spherical, homogenous, non-rotating planet, the plumb bob picks out as vertical the radial direction. Strictly speaking, it is now no longer possible for vertical walls to be parallel: ''all'' verticals intersect. This fact has real practical applications in construction and civil engineering, e.g., the tops of the towers of a suspension bridge are further apart than at the bottom.
When the curvature of the earth is taken into account, the concepts of vertical and horizontal take on yet another meaning. On the surface of a smoothly spherical, homogenous, non-rotating planet, the plumb bob picks out as vertical the radial direction. Strictly speaking, it is now no longer possible for vertical walls to be parallel: ''all'' verticals intersect. This fact has real practical applications in construction and civil engineering, e.g., the tops of the towers of a suspension bridge are further apart than at the bottom.
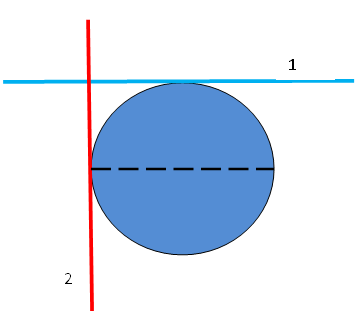 Also, horizontal planes can intersect when they are
Also, horizontal planes can intersect when they are
 In the context of a 1-dimensional orthogonal Cartesian coordinate system on a Euclidean plane, to say that a line is horizontal or vertical, an initial designation has to be made. One can start off by designating the vertical direction, usually labelled the Y direction. The horizontal direction, usually labelled the X direction,
In the context of a 1-dimensional orthogonal Cartesian coordinate system on a Euclidean plane, to say that a line is horizontal or vertical, an initial designation has to be made. One can start off by designating the vertical direction, usually labelled the Y direction. The horizontal direction, usually labelled the X direction,For a definition of "Horizontal axis" see Math Dictionary at www.icoachmath.com
/ref> is then automatically determined. Or, one can do it the other way around, i.e., nominate the ''x''-axis, in which case the ''y''-axis is then automatically determined. There is no special reason to choose the horizontal over the vertical as the initial designation: the two directions are on par in this respect. The following hold in the two-dimensional case: # Through any point P in the plane, there is one and only one ''vertical line'' within the plane and one and only one ''horizontal line'' within the plane. This symmetry breaks down as one moves to the three-dimensional case. # A ''vertical line'' is any line parallel to the vertical direction. A ''horizontal line'' is any line normal to a vertical line. # Horizontal lines do not cross each other. #Vertical lines do not cross each other. Not all of these elementary geometric facts are true in the 3-D context.
 In the 2-dimension case, as mentioned already, the usual designation of the vertical coincides with the
In the 2-dimension case, as mentioned already, the usual designation of the vertical coincides with the
 Although the word horizontal is commonly used in daily life and language (see below), it is subject to many misconceptions.
* The concept of horizontality only makes sense in the context of a clearly measurable gravity field, i.e., in the 'neighborhood' of a planet, star, etc. When the gravity field becomes very weak (the masses are too small or too distant from the point of interest), the notion of being horizontal loses its meaning.
Although the word horizontal is commonly used in daily life and language (see below), it is subject to many misconceptions.
* The concept of horizontality only makes sense in the context of a clearly measurable gravity field, i.e., in the 'neighborhood' of a planet, star, etc. When the gravity field becomes very weak (the masses are too small or too distant from the point of interest), the notion of being horizontal loses its meaning.
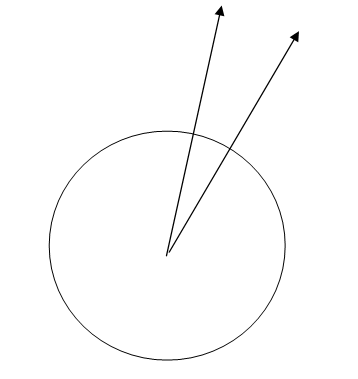 * A plane is horizontal only at the chosen point. Horizontal planes at two separate points are not parallel, they intersect.
* In general, a horizontal plane will only be perpendicular to a
* A plane is horizontal only at the chosen point. Horizontal planes at two separate points are not parallel, they intersect.
* In general, a horizontal plane will only be perpendicular to a  * In reality, the gravity field of a heterogeneous planet such as
* In reality, the gravity field of a heterogeneous planet such as
 The concept of a horizontal plane is thus anything but simple, although, in practice, most of these effects and variations are rather small: they are measurable and can be predicted with great accuracy, but they may not greatly affect our daily life.
This dichotomy between the apparent simplicity of a concept and an actual complexity of defining (and measuring) it in scientific terms arises from the fact that the typical linear scales and dimensions of relevance in daily life are 3
The concept of a horizontal plane is thus anything but simple, although, in practice, most of these effects and variations are rather small: they are measurable and can be predicted with great accuracy, but they may not greatly affect our daily life.
This dichotomy between the apparent simplicity of a concept and an actual complexity of defining (and measuring) it in scientific terms arises from the fact that the typical linear scales and dimensions of relevance in daily life are 3
Video explanations of the terms
{{Authority control Geometry Coordinate systems Geodesy Surveying Orientation (geometry) Position
astronomy
Astronomy () is a natural science that studies celestial objects and phenomena. It uses mathematics, physics, and chemistry in order to explain their origin and evolution. Objects of interest include planets, moons, stars, nebulae, g ...
, geography
Geography (from Greek: , ''geographia''. Combination of Greek words ‘Geo’ (The Earth) and ‘Graphien’ (to describe), literally "earth description") is a field of science devoted to the study of the lands, features, inhabitants, an ...
, and related sciences and contexts, a '' direction'' or ''plane
Plane(s) most often refers to:
* Aero- or airplane, a powered, fixed-wing aircraft
* Plane (geometry), a flat, 2-dimensional surface
Plane or planes may also refer to:
Biology
* Plane (tree) or ''Platanus'', wetland native plant
* ''Planes' ...
'' passing by a given point is said to be vertical if it contains the local gravity direction
The gravity of Earth, denoted by , is the net acceleration that is imparted to objects due to the combined effect of gravitation (from mass distribution within Earth) and the centrifugal force (from the Earth's rotation).
It is a vector quanti ...
at that point.
Conversely, a direction or plane is said to be horizontal if it is perpendicular to the vertical direction.
In general, something that is vertical can be drawn from up to down (or down to up), such as the y-axis in the Cartesian coordinate system.
Historical definition
The word ''horizontal'' is derived from the Latin , which derives from the Greek , meaning 'separating' or 'marking a boundary'. The word ''vertical'' is derived from the late Latin ', which is from the same root as ''vertex'', meaning 'highest point' or more literally the 'turning point' such as in a whirlpool.Girard Desargues
Girard Desargues (; 21 February 1591 – September 1661) was a French mathematician and engineer, who is considered one of the founders of projective geometry. Desargues' theorem, the Desargues graph, and the crater Desargues on the Moon are ...
defined the vertical to be perpendicular to the horizon in his 1636 book ''Perspective''.
Geophysical definition
The plumb line and spirit level
 In physics, engineering and construction, the direction designated as vertical is usually that along which a
In physics, engineering and construction, the direction designated as vertical is usually that along which a plumb-bob
A plumb bob, plumb bob level, or plummet, is a weight, usually with a pointed tip on the bottom, suspended from a string and used as a vertical reference line, or plumb-line. It is a precursor to the spirit level and used to establish a vertic ...
hangs. Alternatively, a spirit level
A spirit level, bubble level, or simply a level, is an instrument designed to indicate whether a surface is horizontal (level) or vertical ( plumb). Different types of spirit levels may be used by carpenters, stonemasons, bricklayers, ...
that exploits the buoyancy of an air bubble and its tendency to go vertically upwards may be used to test for horizontality. A water level device may also be used to establish horizontality.
Modern rotary laser level
In surveying and construction
Construction is a general term meaning the art and science to form objects, systems, or organizations,"Construction" def. 1.a. 1.b. and 1.c. ''Oxford English Dictionary'' Second Edition on CD-ROM (v. 4.0 ...
s that can level themselves automatically are robust sophisticated instruments and work on the same fundamental principle.
The spherical Earth
tangent
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. Mo ...
planes to separated points on the surface of the earth. In particular, a plane tangent to a point on the equator intersects the plane tangent to the North Pole
The North Pole, also known as the Geographic North Pole or Terrestrial North Pole, is the point in the Northern Hemisphere where the Earth's rotation, Earth's axis of rotation meets its surface. It is called the True North Pole to distingu ...
at a right angle. (See diagram).
Furthermore, the equatorial plane is parallel to the tangent plane at the North Pole and as such has claim to be a horizontal plane. But it is. at the same time, a vertical plane for points on the equator. In this sense, a plane can, arguably, be ''both'' horizontal and vertical, horizontal ''at one place'', and vertical ''at another''.
Further complications
For a spinning earth, the plumb line deviates from the radial direction as a function of latitude. Only on the equator and at the North and South Poles does the plumb line align with the local radius. The situation is actually even more complicated because earth is not a homogeneous smooth sphere. It is a non homogeneous, non spherical, knobby planet in motion, and the vertical not only need not lie along a radial, it may even be curved and be varying with time. On a smaller scale, a mountain to one side may deflect the plumb bob away from the truezenith
The zenith (, ) is an imaginary point directly "above" a particular location, on the celestial sphere. "Above" means in the vertical direction ( plumb line) opposite to the gravity direction at that location ( nadir). The zenith is the "high ...
.
On a larger scale the gravitational field of the earth, which is at least approximately radial near the earth, is not radial when it is affected by the moon at higher altitudes.
Independence of horizontal and vertical motions
Neglecting the curvature of the earth, horizontal and vertical motions of a projectile moving under gravity are independent of each other. Vertical displacement of a projectile is not affected by the horizontal component of the launch velocity, and, conversely, the horizontal displacement is unaffected by the vertical component. The notion dates at least as far back as Galileo. When the curvature of the earth is taken into account, the independence of the two motion does ''not'' hold. For example, even a projectile fired in a horizontal direction (i.e., with a zero vertical component) may leave the surface of the spherical earth and indeed escape altogether.Mathematical definition
In two dimensions
/ref> is then automatically determined. Or, one can do it the other way around, i.e., nominate the ''x''-axis, in which case the ''y''-axis is then automatically determined. There is no special reason to choose the horizontal over the vertical as the initial designation: the two directions are on par in this respect. The following hold in the two-dimensional case: # Through any point P in the plane, there is one and only one ''vertical line'' within the plane and one and only one ''horizontal line'' within the plane. This symmetry breaks down as one moves to the three-dimensional case. # A ''vertical line'' is any line parallel to the vertical direction. A ''horizontal line'' is any line normal to a vertical line. # Horizontal lines do not cross each other. #Vertical lines do not cross each other. Not all of these elementary geometric facts are true in the 3-D context.
In three dimensions
In the three-dimensional case, the situation is more complicated as now one has horizontal and vertical planes in addition to horizontal and vertical lines. Consider a point P and designate a direction through P as vertical. A plane which contains P and is normal to the designated direction is the '' horizontal plane'' at P. Any plane going through P, normal to the horizontal plane is a ''vertical plane
In astronomy, geography, and related sciences and contexts, a '' direction'' or ''plane'' passing by a given point is said to be vertical if it contains the local gravity direction at that point.
Conversely, a direction or plane is said to be hor ...
'' at P. Through any point P, there is one and only one horizontal plane but a ''multiplicity'' of vertical planes. This is a new feature that emerges in three dimensions. The symmetry that exists in the two-dimensional case no longer holds.
In the classroom
y-axis
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured i ...
in co-ordinate geometry. This convention can cause confusion in the classroom. For the teacher, writing perhaps on a white board, the ''y''-axis really is vertical in the sense of the plumbline verticality but for the student the axis may well lie on a horizontal table.
Discussion
vertical direction
In astronomy, geography, and related sciences and contexts, a '' direction'' or '' plane'' passing by a given point is said to be vertical if it contains the local gravity direction at that point.
Conversely, a direction or plane is said to be h ...
if both are specifically defined with respect to the same point: a direction is only vertical at the point of reference. Thus both horizontality and verticality are strictly speaking local concepts, and it is always necessary to state to which location the direction or the plane refers to. Note that (1) the same restriction applies to the straight lines contained within the plane: they are horizontal only at the point of reference, and (2) those straight lines contained in the plane but not passing by the reference point are not necessarily horizontal anywhere.
Earth
Earth is the third planet from the Sun and the only astronomical object known to harbor life. While large volumes of water can be found throughout the Solar System, only Earth sustains liquid surface water. About 71% of Earth's surfa ...
is deformed due to the inhomogeneous spatial distribution of materials with different densities. Actual horizontal planes are thus not even parallel even if their reference points are along the same vertical line, since a vertical line is slightly curved.
* At any given location, the total gravitational force is not quite constant over time
Time is the continued sequence of existence and events that occurs in an apparently irreversible succession from the past, through the present, into the future. It is a component quantity of various measurements used to sequence events, ...
, because the objects that generate the gravity are moving. For instance, on Earth the horizontal plane at a given point (as determined by a pair of spirit level
A spirit level, bubble level, or simply a level, is an instrument designed to indicate whether a surface is horizontal (level) or vertical ( plumb). Different types of spirit levels may be used by carpenters, stonemasons, bricklayers, ...
s) changes with the position of the Moon (air, sea and land tide
Tides are the rise and fall of sea levels caused by the combined effects of the gravitational forces exerted by the Moon (and to a much lesser extent, the Sun) and are also caused by the Earth and Moon orbiting one another.
Tide tables ...
s).
* On a rotating planet such as Earth, the strictly gravitational pull of the planet (and other celestial objects such as the Moon, the Sun
The Sun is the star at the center of the Solar System. It is a nearly perfect ball of hot plasma, heated to incandescence by nuclear fusion reactions in its core. The Sun radiates this energy mainly as light, ultraviolet, and infrared radi ...
, etc.) is different from the apparent net force (e.g., on a free-falling object) that can be measured in the laboratory or in the field. This difference is the centrifugal force
In Newtonian mechanics, the centrifugal force is an inertial force (also called a "fictitious" or "pseudo" force) that appears to act on all objects when viewed in a rotating frame of reference. It is directed away from an axis which is parall ...
associated with the planet's rotation. This is a fictitious force: it only arises when calculations or experiments are conducted in non-inertial frames of reference, such as the surface of the Earth.
In general or in practice, something that is horizontal can be drawn from left to right (or right to left), such as the x-axis in the Cartesian coordinate system.
Practical use in daily life
orders of magnitude
An order of magnitude is an approximation of the logarithm of a value relative to some contextually understood reference value, usually 10, interpreted as the base of the logarithm and the representative of values of magnitude one. Logarithmic dis ...
(or more) smaller than the size of the Earth. Hence, the world appears to be flat locally, and horizontal planes in nearby locations appear to be parallel. Such statements are nevertheless approximations; whether they are acceptable in any particular context or application depends on the applicable requirements, in particular in terms of accuracy.
In graphical contexts, such as drawing and drafting and Co-ordinate geometry on rectangular paper, it is very common to associate one of the dimensions of the paper with a horizontal, even though the entire sheet of paper is standing on a flat horizontal (or slanted) table. In this case, the horizontal direction is typically from the left side of the paper to the right side. This is purely conventional (although it is somehow 'natural' when drawing a natural scene as it is seen in reality), and may lead to misunderstandings or misconceptions, especially in an educational context.
See also
* Cartesian coordinate system * Coordinate system * Horizon * Horizontal angle * Horizontal coordinate system *Local tangent plane
Local tangent plane coordinates (LTP), also known as local ellipsoidal system, local geodetic coordinate system, or local vertical, local horizontal coordinates (LVLH), are a spatial reference system based on the tangent plane defined by the local ...
* Northing and easting
* Tilted plane
* Transverse plane
The transverse plane (also known as the horizontal plane, axial plane and transaxial plane) is an anatomical plane that divides the body into superior and inferior sections. It is perpendicular to the coronal and sagittal planes.
List of c ...
* Vertical and horizontal (radio propagation)
In radio propagation, horizontal plane is used to plot an antenna's relative field strength in relation to the ground (which directly affects a station's coverage area) on a polar graph. Normally the maximum of 1.000 or 0 dB is at the top, whi ...
* Vertical circle
In astronomy, a vertical circle is a great circle on the celestial sphere that is perpendicular to the horizon. Therefore, it contains the vertical direction, passing through the zenith and the nadir. There is a vertical circle for any given azim ...
* Vertical position
Vertical position or vertical location, also known as vertical level or simply level, is a position along a vertical direction above or below a given vertical datum (reference level).
Vertical distance or vertical separation is the distance betw ...
* Zenith
The zenith (, ) is an imaginary point directly "above" a particular location, on the celestial sphere. "Above" means in the vertical direction ( plumb line) opposite to the gravity direction at that location ( nadir). The zenith is the "high ...
** Zenith angle
The zenith (, ) is an imaginary point directly "above" a particular location, on the celestial sphere. "Above" means in the vertical direction ( plumb line) opposite to the gravity direction at that location ( nadir). The zenith is the "highe ...
(vertical angle)
References and notes
Further reading
* Brennan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (1998), ''Geometry'', Cambridge: Cambridge University Press, * Murray R Spiegel, (1987), ''Theory and Problems of Theoretical Mechanics'', Singapore, Mcgraw Hill's: Schaum's,External links
Video explanations of the terms
{{Authority control Geometry Coordinate systems Geodesy Surveying Orientation (geometry) Position