Horizon Sales Corporation

The horizon is the apparent line that separates the surface of a celestial body from its sky when viewed from the perspective of an observer on or near the surface of the relevant body. This line divides all viewing directions based on whether it intersects the relevant body's surface or not.

The ''true horizon'' is a theoretical line, which can only be observed to any degree of accuracy when it lies along a relatively smooth surface such as that of Earth's oceans. At many locations, this line is obscured by terrain, and on Earth it can also be obscured by life forms such as trees and/or human constructs such as buildings. The resulting intersection of such obstructions with the sky is called the ''visible horizon''. On Earth, when looking at a sea from a shore, the part of the sea closest to the horizon is called the offing.
Pronounced, "Hor-I-zon".

The true horizon surrounds the observer and it is typically assumed to be a circle, drawn on the surface of a perfectly spherical model of the relevant celestial body. With respect to Earth, the center of the true horizon is below the observer and below sea level. Its distance from the observer varies from day to day due to atmospheric refraction, which is greatly affected by weather conditions. Also, the higher the observer's eyes are from sea level, the farther away the horizon is from the observer. For instance, in standard atmospheric conditions, for an observer with eye level above sea level by , the horizon is at a distance of about .
When observed from very high standpoints, such as a space station, the horizon is much farther away and it encompasses a much larger area of Earth's surface. In this case, the horizon would no longer be a perfect circle, not even a plane curve such as an ellipse, especially when the observer is above the equator, as the Earth's surface can be better modeled as an ellipsoid than as a sphere.

Etymology

The word ''horizon'' derives from the Greek () 'separating circle', where is from the verb ὁρίζω () 'to divide, to separate', which in turn derives from () 'boundary, landmark'.

Appearance and usage

Historically, the distance to the visible horizon has long been vital to survival and successful navigation, especially at sea, because it determined an observer's maximum range of vision and thus of communication, with all the obvious consequences for safety and the transmission of information that this range implied. This importance lessened with the development of the radio and the telegraph, but even today, when flying an aircraft under visual flight rules, a technique called attitude flying is used to control the aircraft, where the pilot uses the visual relationship between the aircraft's nose and the horizon to control the aircraft. Pilots can also retain their spatial orientation by referring to the horizon.

In many contexts, especially perspective drawing, the curvature of the Earth is disregarded and the horizon is considered the theoretical line to which points on any horizontal plane converge (when projected onto the picture plane) as their distance from the observer increases. For observers near sea level, the difference between this ''geometrical horizon'' (which assumes a perfectly flat, infinite ground plane) and the ''true horizon'' (which assumes a spherical Earth surface) is imperceptible to the unaided eye. However, for someone on a hill looking out across the sea, the true horizon will be about a degree below a horizontal line.

In astronomy, the horizon is the horizontal plane through the eyes of the observer. It is the fundamental plane of the horizontal coordinate system, the locus of points that have an altitude of zero degrees. While similar in ways to the geometrical horizon, in this context a horizon may be considered to be a plane in space, rather than a line on a picture plane.

Distance to the horizon

Ignoring the effect of atmospheric refraction, distance to the true horizon from an observer close to the Earth's surface is about

:$d \approx \sqrt \,,$

where ''h'' is height above sea level and ''R'' is the Earth radius.

When ''d'' is measured in kilometres and ''h'' in metres, the distance is

:$d \approx 3.57\sqrt \,,$

where the constant 3.57 has units of km/m^½.

When ''d'' is measured in miles (statute miles i.e. "land miles" of ) and ''h'' in feet, the distance is

:$d \approx \sqrt \approx 1.22\sqrt \,.$

where the constant 1.22 has units of mi/ft^½.

In this equation Earth's surface is assumed to be perfectly spherical, with ''r'' equal to about .

Examples

Assuming no atmospheric refraction and a spherical Earth with radius R=:
* For an observer standing on the ground with ''h'' = , the horizon is at a distance of .
* For an observer standing on the ground with ''h'' = , the horizon is at a distance of .
* For an observer standing on a hill or tower above sea level, the horizon is at a distance of .
* For an observer standing on a hill or tower above sea level, the horizon is at a distance of .
* For an observer standing on the roof of the Burj Khalifa, from ground, and about above sea level, the horizon is at a distance of .
* For an observer atop Mount Everest ( in altitude), the horizon is at a distance of .
* For an observer aboard a commercial passenger plane flying at a typical altitude of , the horizon is at a distance of .
* For a U-2 pilot, whilst flying at its service ceiling , the horizon is at a distance of .

Other planets

On terrestrial planets and other solid celestial bodies with negligible atmospheric effects, the distance to the horizon for a "standard observer" varies as the square root of the planet's radius. Thus, the horizon on Mercury is 62% as far away from the observer as it is on Earth, on Mars the figure is 73%, on the Moon the figure is 52%, on Mimas the figure is 18%, and so on.

Derivation

If the Earth is assumed to be a featureless sphere (rather than an oblate spheroid) with no atmospheric refraction, then the distance to the horizon can easily be calculated.

The tangent-secant theorem states that
:$\mathrm^2 = \mathrm \times \mathrm \,.$
Make the following substitutions:
* ''d'' = OC = distance to the horizon
* ''D'' = AB = diameter of the Earth
* ''h'' = OB = height of the observer above sea level
* ''D+h'' = OA = diameter of the Earth plus height of the observer above sea level,

with ''d, D,'' and ''h'' all measured in the same units. The formula now becomes
:$d^2 = h(D+h)\,\!$
or
:$d = \sqrt =\sqrt\,,$

where ''R'' is the radius of the Earth.

The same equation can also be derived using the Pythagorean theorem.
At the horizon, the line of sight is a tangent to the Earth and is also perpendicular to Earth's radius.
This sets up a right triangle, with the sum of the radius and the height as the hypotenuse.
With

* ''d'' = distance to the horizon
* ''h'' = height of the observer above sea level
* ''R'' = radius of the Earth

referring to the second figure at the right leads to the following:

:$(R+h)^2 = R^2 + d^2 \,\!$
:$R^2 + 2Rh + h^2 = R^2 + d^2 \,\!$
:$d = \sqrt \,.$

The exact formula above can be expanded as:

:$d = \sqrt \,,$

where ''R'' is the radius of the Earth (''R'' and ''h'' must be in the same units). For example,
if a satellite is at a height of 2000 km, the distance to the horizon is ;
neglecting the second term in parentheses would give a distance of , a 7% error.

Approximation

If the observer is close to the surface of the earth, then it is valid to disregard ''h'' in the term , and the formula becomes-

:$d = \sqrt \,.$

Using kilometres for ''d'' and ''R'', and metres for ''h'', and taking the radius of the Earth as 6371 km, the distance to the horizon is

:$d \approx \sqrt \approx 3.570\sqrt \,$.

Using imperial units, with ''d'' and ''R'' in statute miles (as commonly used on land), and ''h'' in feet, the distance to the horizon is

:$d \approx \sqrt \approx \sqrt \approx 1.22 \sqrt$.

If ''d'' is in nautical miles, and ''h'' in feet, the constant factor is about 1.06, which is close enough to 1 that it is often ignored, giving:

:$d \approx \sqrt h$

These formulas may be used when ''h'' is much smaller than the radius of the Earth (6371 km or 3959 mi), including all views from any mountaintops, airplanes, or high-altitude balloons. With the constants as given, both the metric and imperial formulas are precise to within 1% (see the next section for how to obtain greater precision).
If ''h'' is significant with respect to ''R'', as with most satellites, then the approximation is no longer valid, and the exact formula is required.

Other measures

Arc distance

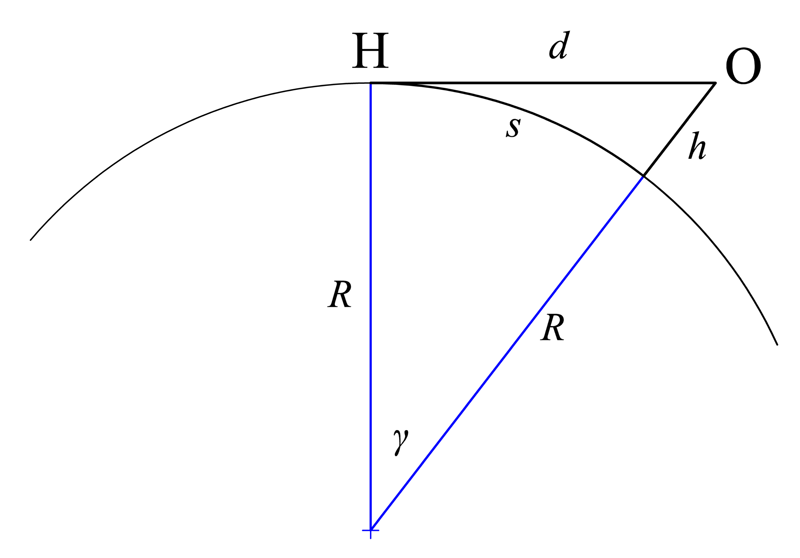
Another relationship involves the great-circle distance ''s'' along the arc over the curved surface of the Earth to the horizon; with ''γ'' in radians,

:$s = R \gamma \,;$

then

:$\cos \gamma = \cos\frac=\frac\,.$

Solving for ''s'' gives

:$s=R\cos^\frac \,.$

The distance ''s'' can also be expressed in terms of the line-of-sight distance ''d''; from the second figure at the right,

:$\tan \gamma = \frac \,;$

substituting for ''γ'' and rearranging gives

:$s=R\tan^\frac \,.$

The distances ''d'' and ''s'' are nearly the same when the height of the object is negligible compared to the radius (that is, ''h'' ≪ ''R'').

Zenith angle

When the observer is elevated, the horizon zenith angle can be greater than 90°. The maximum visible zenith angle occurs when the ray is tangent to Earth's surface; from triangle OCG in the figure at right,

:$\cos \gamma =\frac$

where $h$ is the observer's height above the surface and $\gamma$ is the angular dip of the horizon. It is related to the horizon zenith angle $z$ by:

:$z = \gamma +90^\circ$

For a non-negative height $h$, the angle $z$ is always ≥ 90°.

Objects above the horizon

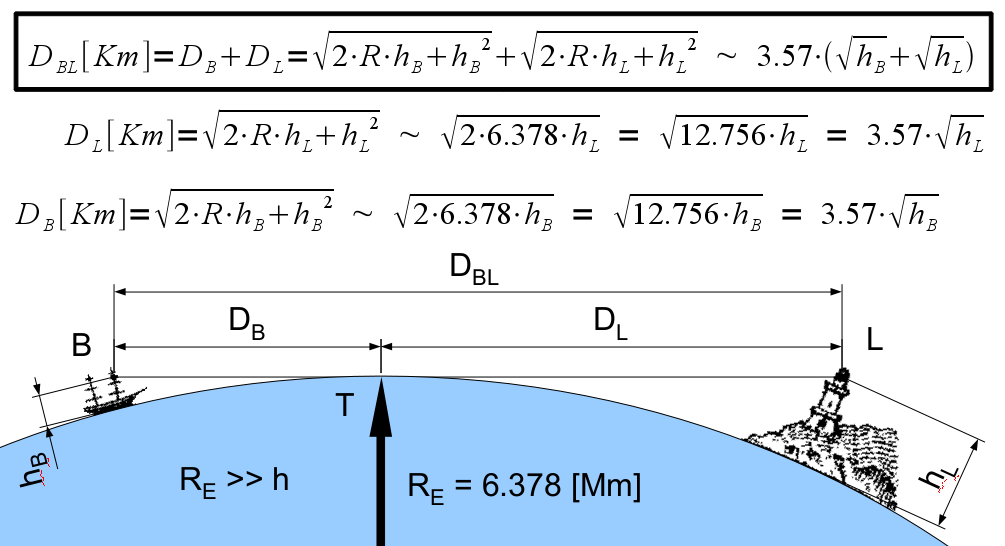
To compute the greatest distance at which an observer can see the top of an object above the horizon, compute the distance to the horizon for a hypothetical observer on top of that object, and add it to the real observer's distance to the horizon. For example, for an observer with a height of 1.70 m standing on the ground, the horizon is 4.65 km away. For a tower with a height of 100 m, the horizon distance is 35.7 km. Thus an observer on a beach can see the top of the tower as long as it is not more than 40.35 km away. Conversely, if an observer on a boat () can just see the tops of trees on a nearby shore (), the trees are probably about 16 km away.

Referring to the figure at the right, the top of the lighthouse will be visible to a lookout in a crow's nest at the top of a mast of the boat if
:$D_\mathrm < 3.57\,(\sqrt + \sqrt) \,,$
where ''D''_BL is in kilometres and ''h''_B and ''h''_L are in metres.

As another example, suppose an observer, whose eyes are two metres above the level ground, uses binoculars to look at a distant building which he knows to consist of thirty storeys, each 3.5 metres high. He counts the storeys he can see, and finds there are only ten. So twenty storeys or 70 metres of the building are hidden from him by the curvature of the Earth. From this, he can calculate his distance from the building:

:$D \approx 3.57(\sqrt+\sqrt)$

which comes to about 35 kilometres.

It is similarly possible to calculate how much of a distant object is visible above the horizon. Suppose an observer's eye is 10 metres above sea level, and he is watching a ship that is 20 km away. His horizon is:

:$3.57 \sqrt$

kilometres from him, which comes to about 11.3 kilometres away. The ship is a further 8.7 km away. The height of a point on the ship that is just visible to the observer is given by:

:$h\approx\left(\frac\right)^2$

which comes to almost exactly six metres. The observer can therefore see that part of the ship that is more than six metres above the level of the water. The part of the ship that is below this height is hidden from him by the curvature of the Earth. In this situation, the ship is said to be hull-down.

Effect of atmospheric refraction

Due to atmospheric refraction the distance to the visible horizon is further than the distance based on a simple geometric calculation. If the ground (or water) surface is colder than the air above it, a cold, dense layer of air forms close to the surface, causing light to be refracted downward as it travels, and therefore, to some extent, to go around the curvature of the Earth. The reverse happens if the ground is hotter than the air above it, as often happens in deserts, producing mirages. As an approximate compensation for refraction, surveyors measuring distances longer than 100 meters subtract 14% from the calculated curvature error and ensure lines of sight are at least 1.5 metres from the ground, to reduce random errors created by refraction.

If the Earth were an airless world like the Moon, the above calculations would be accurate. However, Earth has an atmosphere of air, whose density and refractive index vary considerably depending on the temperature and pressure. This makes the air refract light to varying extents, affecting the appearance of the horizon. Usually, the density of the air just above the surface of the Earth is greater than its density at greater altitudes. This makes its refractive index greater near the surface than at higher altitudes, which causes light that is travelling roughly horizontally to be refracted downward. This makes the actual distance to the horizon greater than the distance calculated with geometrical formulas. With standard atmospheric conditions, the difference is about 8%. This changes the factor of 3.57, in the metric formulas used above, to about 3.86. For instance, if an observer is standing on seashore, with eyes 1.70 m above sea level, according to the simple geometrical formulas given above the horizon should be 4.7 km away. Actually, atmospheric refraction allows the observer to see 300 metres farther, moving the true horizon 5 km away from the observer.

This correction can be, and often is, applied as a fairly good approximation when atmospheric conditions are close to standard. When conditions are unusual, this approximation fails. Refraction is strongly affected by temperature gradients, which can vary considerably from day to day, especially over water. In extreme cases, usually in springtime, when warm air overlies cold water, refraction can allow light to follow the Earth's surface for hundreds of kilometres. Opposite conditions occur, for example, in deserts, where the surface is very hot, so hot, low-density air is below cooler air. This causes light to be refracted upward, causing mirage effects that make the concept of the horizon somewhat meaningless. Calculated values for the effects of refraction under unusual conditions are therefore only approximate. Nevertheless, attempts have been made to calculate them more accurately than the simple approximation described above.

Outside the visual wavelength range, refraction will be different. For radar (e.g. for wavelengths 300 to 3 mm i.e. frequencies between 1 and 100 GHz) the radius of the Earth may be multiplied by 4/3 to obtain an effective radius giving a factor of 4.12 in the metric formula i.e. the radar horizon will be 15% beyond the geometrical horizon or 7% beyond the visual. The 4/3 factor is not exact, as in the visual case the refraction depends on atmospheric conditions.

;Integration method—Sweer
If the density profile of the atmosphere is known, the distance ''d'' to the horizon is given by

:$d=\left( \psi +\delta \right) \,,$

where ''R''_E is the radius of the Earth, ''ψ'' is the dip of the horizon and ''δ'' is the refraction of the horizon. The dip is determined fairly simply from

:$\cos \psi = \frac \,,$

where ''h'' is the observer's height above the Earth, ''μ'' is the index of refraction of air at the observer's height, and ''μ''₀ is the index of refraction of air at Earth's surface.

The refraction must be found by integration of

:$\delta =-\int_^ \,,$

where $\phi\,\!$ is the angle between the ray and a line through the center of the Earth. The angles ''ψ'' and $\phi\,\!$ are related by

:$\phi =90^\circ -\psi \,.$

;Simple method—Young
A much simpler approach, which produces essentially the same results as the first-order approximation described above, uses the geometrical model but uses a radius . The distance to the horizon is then

:$d=\sqrt \,.$

Taking the radius of the Earth as 6371 km, with ''d'' in km and ''h'' in m,

:$d \approx 3.86 \sqrt \,;$

with ''d'' in mi and ''h'' in ft,

:$d \approx 1.32 \sqrt \,.$

Results from Young's method are quite close to those from Sweer's method, and are sufficiently accurate for many purposes.

Curvature of the horizon

From a point above Earth's surface, the horizon appears slightly convex; it is a circular arc. The following formula expresses the basic geometrical relationship between this visual curvature $\kappa$, the altitude $h$, and Earth's radius $R$:
:$\kappa=\sqrt\$

The curvature is the reciprocal of the curvature angular radius in radians. A curvature of 1.0 appears as a circle of an angular radius of 57.3° corresponding to an altitude of approximately above Earth's surface. At an altitude of , the cruising altitude of a typical airliner, the mathematical curvature of the horizon is about 0.056, the same curvature of the rim of circle with a radius of 10 m that is viewed from 56 cm directly above the center of the circle. However, the apparent curvature is less than that due to refraction of light by the atmosphere and the obscuration of the horizon by high cloud layers that reduce the altitude above the visual surface.

Vanishing points

The horizon is a key feature of the picture plane in the science of graphical perspective. Assuming the picture plane stands vertical to ground, and ''P'' is the perpendicular projection of the eye point ''O'' on the picture plane, the horizon is defined as the horizontal line through ''P''. The point ''P'' is the vanishing point of lines perpendicular to the picture. If ''S'' is another point on the horizon, then it is the vanishing point for all lines parallel to ''OS''. But Brook Taylor (1719) indicated that the horizon plane determined by ''O'' and the horizon was like any other plane:
:The term of Horizontal Line, for instance, is apt to confine the Notions of a Learner to the Plane of the Horizon, and to make him imagine, that that Plane enjoys some particular Privileges, which make the Figures in it more easy and more convenient to be described, by the means of that Horizontal Line, than the Figures in any other plane;…But in this Book I make no difference between the Plane of the Horizon, and any other Plane whatsoever...
The peculiar geometry of perspective where parallel lines converge in the distance, stimulated the development of projective geometry which posits a point at infinity where parallel lines meet. In her book ''Geometry of an Art'' (2007), Kirsti Andersen described the evolution of perspective drawing and science up to 1800, noting that vanishing points need not be on the horizon. In a chapter titled "Horizon", John Stillwell recounted how projective geometry has led to incidence geometry, the modern abstract study of line intersection. Stillwell also ventured into foundations of mathematics in a section titled "What are the Laws of Algebra ?" The "algebra of points", originally given by Karl von Staudt deriving the axioms of a field was deconstructed in the twentieth century, yielding a wide variety of mathematical possibilities. Stillwell states
:This discovery from 100 years ago seems capable of turning mathematics upside down, though it has not yet been fully absorbed by the mathematical community. Not only does it defy the trend of turning geometry into algebra, it suggests that both geometry and algebra have a simpler foundation than previously thought.

See also

References

Further reading

*

{{Authority control

Horizontal coordinate system
Astronomical coordinate systems