Hirsch Conjecture

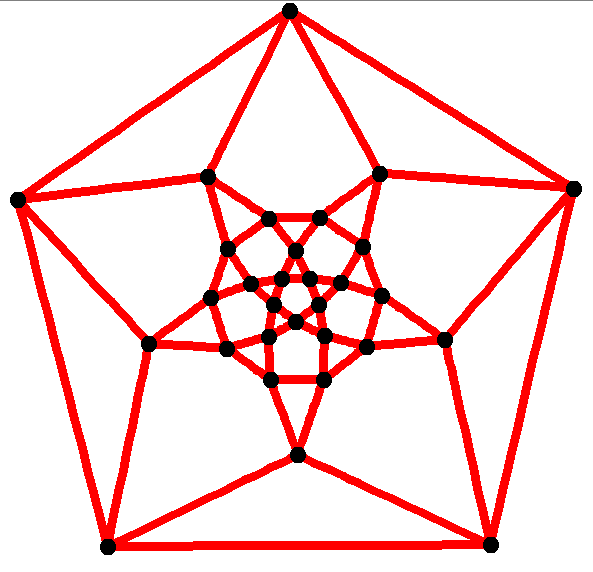In mathematical programming and polyhedral combinatorics, the Hirsch conjecture is the statement that the edge-vertex graph of an ''n''-facet polytope in ''d''-dimensional Euclidean space has diameter no more than ''n'' − ''d''. That is, any two vertices of the polytope must be connected to each other by a path of length at most ''n'' − ''d''. The conjecture was first put forth in a letter by to George B. Dantzig in 1957 and was motivated by the analysis of the simplex method in linear programming, as the diameter of a polytope provides a lower bound on the number of steps needed by the simplex method. The conjecture is now known to be false in general.

The Hirsch conjecture was proven for ''d'' < 4 and for various special cases, while the best known upper bounds on the diameter are only sub-exponential in ''n'' and ''d''. After more than fifty years, a counter-example was announced in May 2010 by Francisco Santos Leal, from the University of Cantabria... The result was presented at the conference ''100 Years in Seattle: the mathematics of Klee and Grünbaum'' and appeared in ''Annals of Mathematics''. Specifically, the paper presented a 43-dimensional polytope of 86 facets with a diameter of more than 43. The counterexample has no direct consequences for the analysis of the simplex method, as it does not rule out the possibility of a larger but still linear or polynomial number of steps.

Various equivalent formulations of the problem had been given, such as the ''d''-step conjecture, which states that the diameter of any 2''d''-facet polytope in ''d''-dimensional Euclidean space is no more than ''d''; Santos Leal's counterexample also disproves this conjecture., p. 84..

Statement of the conjecture

The ''graph'' of a convex polytope $P$ is any graph whose vertices are in bijection with the vertices of $P$ in such a way that any two vertices of the graph are joined by an edge if and only if the two corresponding vertices of $P$ are joined by an edge of the polytope. The diameter of $P$, denoted $\delta(P)$, is the diameter of any one of its graphs. These definitions are well-defined since any two graphs of the same polytope must be isomorphic as graphs. We may then state the Hirsch conjecture as follows:

Conjecture Let $P$ be a ''d''-dimensional convex polytope with ''n'' facets. Then $\delta(P)\leq n-d$.

For example, a cube in three dimensions has six facets. The Hirsch conjecture then indicates that the diameter of this cube cannot be greater than three. Accepting the conjecture would imply that any two vertices of the cube may be connected by a path from vertex to vertex using, at most, three steps. For all polytopes of dimension at least 8, this bound is actually optimal; no polytope of dimension $d\geq 8$ has a diameter less than ''n-d'', with ''n'' being the number of its facets, as before. In other words, for nearly all cases, the conjecture provides the minimum number of steps needed to join any two vertices of a polytope by a path along its edges. Since the simplex method essentially operates by constructing a path from some vertex of the feasible region to an optimal point, the Hirsch conjecture would provide a lower bound needed for the simplex method to terminate in the worst case scenario.

The Hirsch conjecture is a special case of the ''polynomial Hirsch conjecture'', which claims that there exists some positive integer ''k'' such that, for all polytopes $P$, $\delta(P)=O(n^k)$, where ''n'' is the number of facets of ''P''.

Progress and intermediate results

The Hirsch conjecture has been proven true for a number of cases. For example, any polytope with dimension 3 or lower satisfies the conjecture. Any ''d''-dimensional polytope with ''n'' facets such that $n-d\leq 6$ satisfies the conjecture as well.

Other attempts to solve the conjecture manifested out of a desire to formulate a different problem whose solution would imply the Hirsch conjecture. One example of particular importance is the ''d-step conjecture'', a relaxation of the Hirsch conjecture that has actually been shown to be equivalent to it.

Theorem The following statements are equivalent:
# $\delta(P)\leq n-d$ for all ''d''-dimensional polytopes $P$ with ''n'' facets.
# $\delta(P)\leq d$ for all ''d''-dimensional polytopes $P$ with ''2d'' facets.

In other words, in order to prove or disprove the Hirsch conjecture, one only needs to consider polytopes with exactly twice as many facets as its dimension. Another significant relaxation is that the Hirsch conjecture holds for all polytopes if and only if it holds for all simple polytopes.

Counterexample

Unfortunately, the Hirsch conjecture is not true in all cases, as shown by Francisco Santos in 2011. Santos' explicit construction of a counterexample comes both from the fact that the conjecture may be relaxed to only consider simple polytopes, and from equivalence between the Hirsch and ''d''-step conjectures. In particular, Santos produces his counterexample by examining a particular class of polytopes called ''spindles''.

Definition A ''d''-spindle is a ''d''-dimensional polytope $P$ for which there exist a pair of distinct vertices such that every facet of $P$ contains exactly one of these two vertices.

The length of the shortest path between these two vertices is called the ''length'' of the spindle. The disproof of the Hirsch conjecture relies on the following theorem, referred to as the ''strong d-step theorem for spindles''.

Theorem (Santos) Let $P$ be a ''d''-spindle. Let ''n'' be the number of its facets, and let ''l'' be its length. Then there exists an $(n-d)$-spindle, $P'$, with $2n-2d$ facets and a length bounded below by $l+n-2d$. In particular, if $l>d$, then $P'$ violates the ''d''-step conjecture.

Santos then proceeds to construct a 5-dimensional spindle with length 6, hence proving that there exists another spindle that serves as a counterexample to the Hirsch conjecture. The first of these two spindles has 48 facets and 322 vertices, while the spindle that actually disproves the conjecture has 86 facets and is 43-dimensional. This counterexample does not disprove the polynomial Hirsch conjecture, which remains an open problem.

Notes

References

*. Reprinted in the series ''Princeton Landmarks in Mathematics'', Princeton University Press, 1998.
*
*.
*.
*.
*.
*
*.

{{Disproved conjectures

Polyhedral combinatorics
Conjectures
Disproved conjectures
Linear programming