Hilbert's Sixth Problem on:
[Wikipedia]
[Google]
[Amazon]
Hilbert's sixth problem is to 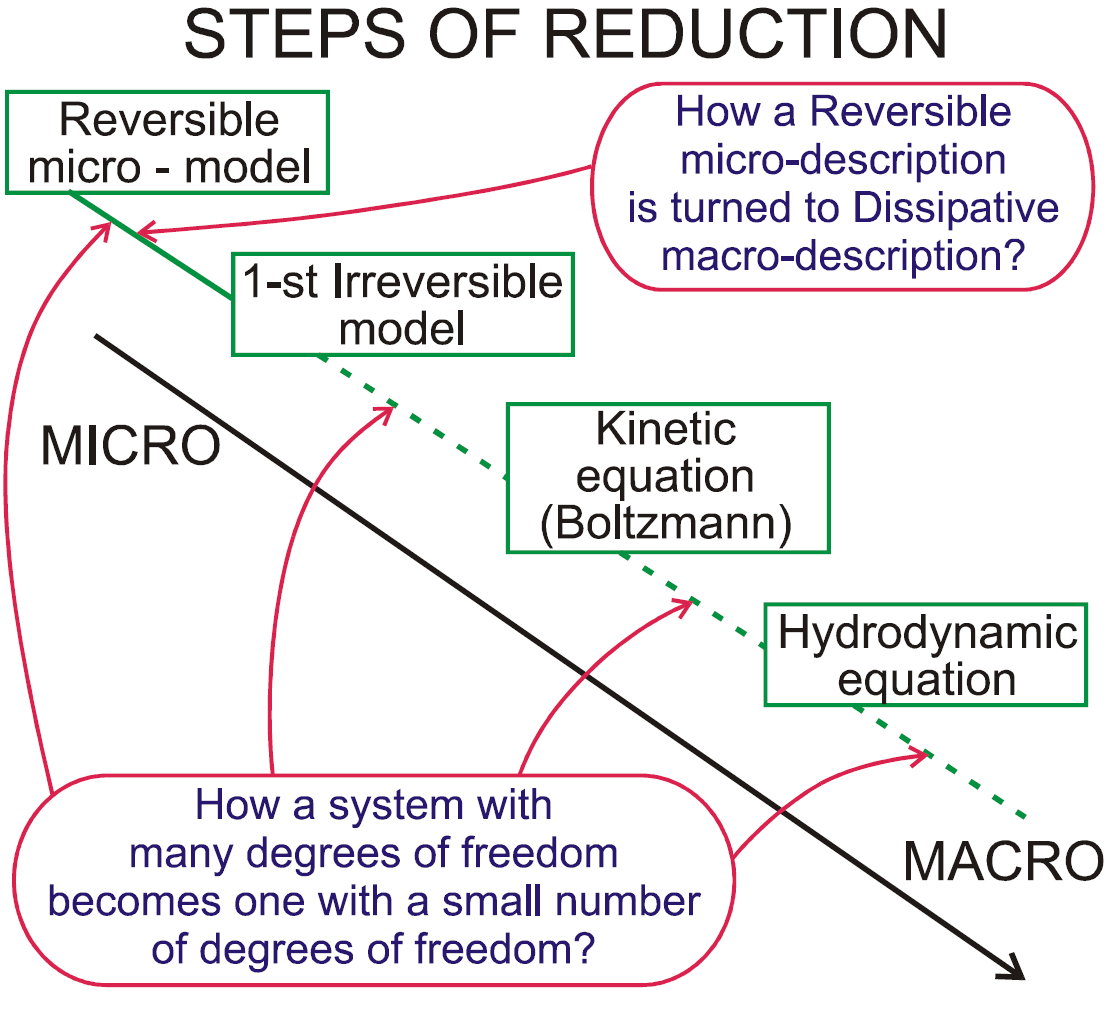 :6. Mathematical Treatment of the Axioms of Physics. The investigations on the foundations of geometry suggest the problem: ''To treat in the same manner, by means of axioms, those physical sciences in which already today mathematics plays an important part; in the first rank are the theory of probabilities and mechanics.''
Hilbert gave the further explanation of this problem and its possible specific forms:
:"As to the axioms of the theory of probabilities, it seems to me desirable that their logical investigation should be accompanied by a rigorous and satisfactory development of the method of mean values in mathematical physics, and in particular in the kinetic theory of gases. ... Boltzmann's work on the principles of mechanics suggests the problem of developing mathematically the limiting processes, there merely indicated, which lead from the atomistic view to the laws of motion of continua."
:6. Mathematical Treatment of the Axioms of Physics. The investigations on the foundations of geometry suggest the problem: ''To treat in the same manner, by means of axioms, those physical sciences in which already today mathematics plays an important part; in the first rank are the theory of probabilities and mechanics.''
Hilbert gave the further explanation of this problem and its possible specific forms:
:"As to the axioms of the theory of probabilities, it seems to me desirable that their logical investigation should be accompanied by a rigorous and satisfactory development of the method of mean values in mathematical physics, and in particular in the kinetic theory of gases. ... Boltzmann's work on the principles of mechanics suggests the problem of developing mathematically the limiting processes, there merely indicated, which lead from the atomistic view to the laws of motion of continua."
David Hilbert, Mathematical Problems, Problem 6, in English translation
{{Authority control #06 Unsolved problems in physics
axiom
An axiom, postulate, or assumption is a statement that is taken to be true, to serve as a premise or starting point for further reasoning and arguments. The word comes from the Ancient Greek word (), meaning 'that which is thought worthy or f ...
atize those branches of physics in which mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
is prevalent. It occurs on the widely cited list of Hilbert's problems
Hilbert's problems are 23 problems in mathematics published by German mathematician David Hilbert in 1900. They were all unsolved at the time, and several proved to be very influential for 20th-century mathematics. Hilbert presented ten of the pro ...
in mathematics that he presented in the year 1900. In its common English translation, the explicit statement reads:
 :6. Mathematical Treatment of the Axioms of Physics. The investigations on the foundations of geometry suggest the problem: ''To treat in the same manner, by means of axioms, those physical sciences in which already today mathematics plays an important part; in the first rank are the theory of probabilities and mechanics.''
Hilbert gave the further explanation of this problem and its possible specific forms:
:"As to the axioms of the theory of probabilities, it seems to me desirable that their logical investigation should be accompanied by a rigorous and satisfactory development of the method of mean values in mathematical physics, and in particular in the kinetic theory of gases. ... Boltzmann's work on the principles of mechanics suggests the problem of developing mathematically the limiting processes, there merely indicated, which lead from the atomistic view to the laws of motion of continua."
:6. Mathematical Treatment of the Axioms of Physics. The investigations on the foundations of geometry suggest the problem: ''To treat in the same manner, by means of axioms, those physical sciences in which already today mathematics plays an important part; in the first rank are the theory of probabilities and mechanics.''
Hilbert gave the further explanation of this problem and its possible specific forms:
:"As to the axioms of the theory of probabilities, it seems to me desirable that their logical investigation should be accompanied by a rigorous and satisfactory development of the method of mean values in mathematical physics, and in particular in the kinetic theory of gases. ... Boltzmann's work on the principles of mechanics suggests the problem of developing mathematically the limiting processes, there merely indicated, which lead from the atomistic view to the laws of motion of continua."
History
David Hilbert
David Hilbert (; ; 23 January 1862 – 14 February 1943) was a German mathematician, one of the most influential mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many a ...
himself devoted much of his research to the sixth problem; in particular, he worked in those fields of physics that arose after he stated the problem.
In the 1910s, celestial mechanics evolved into general relativity. Hilbert and Emmy Noether corresponded extensively with Albert Einstein on the formulation of the theory.
In the 1920s, mechanics of microscopic systems evolved into quantum mechanics. Hilbert, with the assistance of John von Neumann, L. Nordheim, and E. P. Wigner
Eugene Paul "E. P." Wigner ( hu, Wigner Jenő Pál, ; November 17, 1902 – January 1, 1995) was a Hungarian-American theoretical physicist who also contributed to mathematical physics. He received the Nobel Prize in Physics in 1963 "for his ...
, worked on the axiomatic basis of quantum mechanics (see Hilbert space
In mathematics, Hilbert spaces (named after David Hilbert) allow generalizing the methods of linear algebra and calculus from (finite-dimensional) Euclidean vector spaces to spaces that may be infinite-dimensional. Hilbert spaces arise natural ...
). At the same time, but independently, Dirac formulated quantum mechanics in a way that is close to an axiomatic system, as did Hermann Weyl
Hermann Klaus Hugo Weyl, (; 9 November 1885 – 8 December 1955) was a German mathematician, theoretical physicist and philosopher. Although much of his working life was spent in Zürich, Switzerland, and then Princeton, New Jersey, he is assoc ...
with the assistance of Erwin Schrödinger.
In the 1930s, probability theory was put on an axiomatic basis by Andrey Kolmogorov, using measure theory
In mathematics, the concept of a measure is a generalization and formalization of geometrical measures ( length, area, volume) and other common notions, such as mass and probability of events. These seemingly distinct concepts have many simil ...
.
Since the 1960s, following the work of Arthur Wightman
Arthur Strong Wightman (March 30, 1922 – January 13, 2013) was an American mathematical physicist. He was one of the founders of the axiomatic approach to quantum field theory, and originated the set of Wightman axioms. With his rigorous treatm ...
and Rudolf Haag, modern quantum field theory
In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines classical field theory, special relativity, and quantum mechanics. QFT is used in particle physics to construct physical models of subatomic particles and ...
can also be considered close to an axiomatic description.
In the 1990s-2000s the problem of "the limiting processes, there merely indicated, which lead from the atomistic view to the laws of motion of continua" was approached by many groups of mathematicians. Main recent results are summarized by Laure Saint-Raymond, Marshall Slemrod, Alexander N. Gorban and Ilya Karlin
Ilya, Iliya, Ilia, Ilja, or Ilija (russian: Илья́, Il'ja, , or russian: Илия́, Ilija, ; uk, Ілля́, Illia, ; be, Ілья́, Iĺja ) is the East Slavic form of the male Hebrew name Eliyahu (Eliahu), meaning "My God is Yahu/ Jah." ...
.
Status
Hilbert’s sixth problem was a proposal to expand the axiomatic method outside the existing mathematical disciplines, to physics and beyond. This expansion requires development of semantics of physics with formal analysis of the notion of physical reality that should be done. Two fundamental theories capture the majority of the fundamental phenomena of physics: *Quantum field theory
In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines classical field theory, special relativity, and quantum mechanics. QFT is used in particle physics to construct physical models of subatomic particles and ...
, which provides the mathematical framework for the Standard Model
The Standard Model of particle physics is the theory describing three of the four known fundamental forces (electromagnetism, electromagnetic, weak interaction, weak and strong interactions - excluding gravity) in the universe and classifying a ...
;
* General relativity, which describes space-time and gravity at macroscopic scale.
Hilbert considered general relativity as an essential part of the foundation of physics. However, quantum field theory is not logically consistent with general relativity, indicating the need for a still-unknown theory of quantum gravity
Quantum gravity (QG) is a field of theoretical physics that seeks to describe gravity according to the principles of quantum mechanics; it deals with environments in which neither gravitational nor quantum effects can be ignored, such as in the vi ...
, where the semantics of physics is expected to play a central role. Hilbert's sixth problem thus remains open.Theme issue
See also
*Wightman axioms
In mathematical physics, the Wightman axioms (also called Gårding–Wightman axioms), named after Arthur Wightman, are an attempt at a mathematically rigorous formulation of quantum field theory. Arthur Wightman formulated the axioms in the ear ...
* Constructive quantum field theory
Notes
References
* *External links
David Hilbert, Mathematical Problems, Problem 6, in English translation
{{Authority control #06 Unsolved problems in physics