Hexagonal Tortoise Problem on:
[Wikipedia]
[Google]
[Amazon]
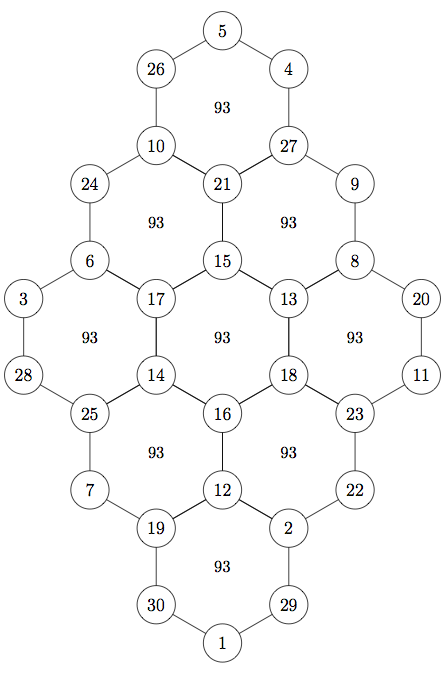The hexagonal tortoise problem () was invented by Korean aristocrat and mathematician Choi Seok-jeong (1646–1715). It is a mathematical problem that involves a hexagonal lattice, like the hexagonal pattern on some tortoises' shells, to the (''N'') vertices of which must be assigned integers (from 1 to ''N'') in such a way that the sum of all integers at the vertices of each hexagon is the same. The problem has apparent similarities to a
The hexagonal tortoise problem () was invented by Korean aristocrat and mathematician Choi Seok-jeong (1646–1715). It is a mathematical problem that involves a hexagonal lattice, like the hexagonal pattern on some tortoises' shells, to the (''N'') vertices of which must be assigned integers (from 1 to ''N'') in such a way that the sum of all integers at the vertices of each hexagon is the same. The problem has apparent similarities to a magic square
In recreational mathematics, a square array of numbers, usually positive integers, is called a magic square if the sums of the numbers in each row, each column, and both main diagonals are the same. The 'order' of the magic square is the number ...
although it is a vertex-magic format rather than an edge-magic form or the more typical rows-of-cells form.
His book, ''Gusuryak'', contains many mathematical discoveries.
References
Sources used
* Recreational mathematics Magic shapes {{numtheory-stub