Hexagonal fast Fourier transform on:
[Wikipedia]
[Google]
[Amazon]
The
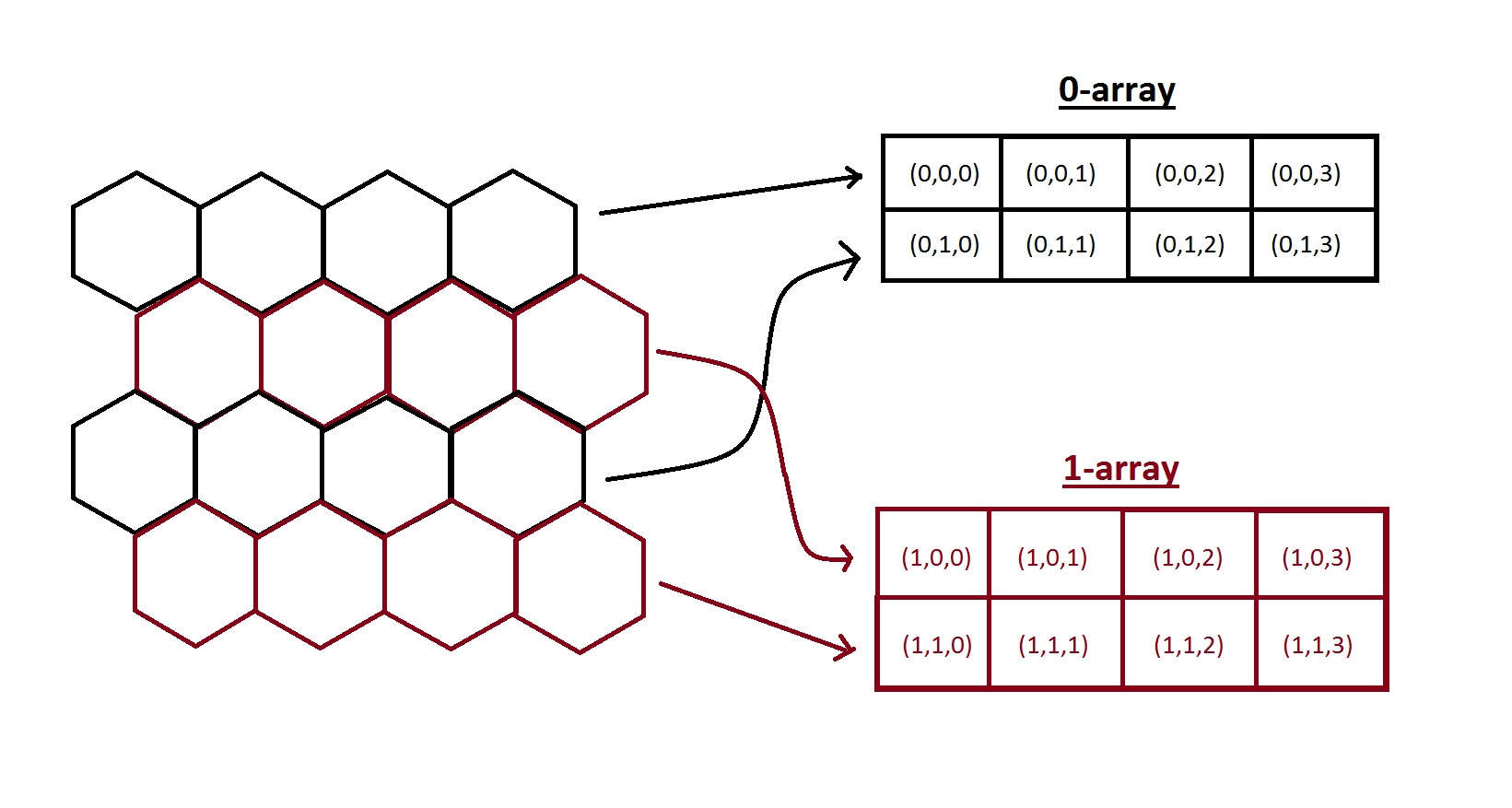 The hexagonal efficient coordinate system (formerly known as array set addressing (ASA)) was developed based on the fact that a hexagonal grid can be represented as a combination of two interleaved rectangular arrays.Nicholas I. Rummelt, 2010, Array Set Addressing: Enabling Efficient Hexagonally Sampled Image Processing, Ph.D. thesis, University of Florida It is easy to address each individual array using familiar integer-valued row and column indices and the individual arrays are distinguished by a single binary coordinate. Therefore, a full address for any point in the hexagonal grid can be uniquely represented by three coordinates.
::
where the coordinates ''a'', ''r'' and ''c'' represent the array, row and column respectively. The figure shows how the hexagonal grid is represented by two interleaved rectangular arrays in HECS coordinates.
The hexagonal efficient coordinate system (formerly known as array set addressing (ASA)) was developed based on the fact that a hexagonal grid can be represented as a combination of two interleaved rectangular arrays.Nicholas I. Rummelt, 2010, Array Set Addressing: Enabling Efficient Hexagonally Sampled Image Processing, Ph.D. thesis, University of Florida It is easy to address each individual array using familiar integer-valued row and column indices and the individual arrays are distinguished by a single binary coordinate. Therefore, a full address for any point in the hexagonal grid can be uniquely represented by three coordinates.
::
where the coordinates ''a'', ''r'' and ''c'' represent the array, row and column respectively. The figure shows how the hexagonal grid is represented by two interleaved rectangular arrays in HECS coordinates.
fast Fourier transform
A fast Fourier transform (FFT) is an algorithm that computes the discrete Fourier transform (DFT) of a sequence, or its inverse (IDFT). A Fourier transform converts a signal from its original domain (often time or space) to a representation in ...
(FFT) is an important tool in the fields of image and signal processing. The hexagonal fast Fourier transform (HFFT) uses existing FFT routines to compute the discrete Fourier transform
In mathematics, the discrete Fourier transform (DFT) converts a finite sequence of equally-spaced Sampling (signal processing), samples of a function (mathematics), function into a same-length sequence of equally-spaced samples of the discre ...
(DFT) of images that have been captured with hexagonal sampling.James B. Birdsong, Nicholas I. Rummelt, "The Hexagonal Fast Fourier Transform", 2016 IEEE International Conference on Image Processing (ICIP), pp. 1809–1812, The hexagonal grid serves as the optimal sampling lattice for isotropically band-limited
Bandlimiting is the process of reducing a signal’s energy outside a specific frequency range, keeping only the desired part of the signal’s spectrum. This technique is crucial in signal processing and communications to ensure signals stay cl ...
two-dimensional signals and has a sampling efficiency which is 13.4% greater than the sampling efficiency obtained from rectangular sampling.R. M. Mersereau, June 1979, "The Processing of Hexagonally Sampled Two-Dimensional Signals", Proceedings of the IEEE, vol. 67, no. 6, pp. 930–949 Several other advantages of hexagonal sampling include consistent connectivity, higher symmetry
Symmetry () in everyday life refers to a sense of harmonious and beautiful proportion and balance. In mathematics, the term has a more precise definition and is usually used to refer to an object that is Invariant (mathematics), invariant und ...
, greater angular resolution
Angular resolution describes the ability of any image-forming device such as an Optical telescope, optical or radio telescope, a microscope, a camera, or an Human eye, eye, to distinguish small details of an object, thereby making it a major det ...
, and equidistant
A point is said to be equidistant from a set of objects if the distances between that point and each object in the set are equal.
In two-dimensional Euclidean geometry, the locus of points equidistant from two given (different) points is t ...
neighbouring pixels
In digital imaging, a pixel (abbreviated px), pel, or picture element is the smallest addressable element in a raster image, or the smallest addressable element in a dot matrix display device. In most digital display devices, pixels are the sma ...
.W. E. Snyder, 1999, H. Qi, and W. Sander, "A coordinate system for hexagonal pixels", in Proc. SPIE Medical Imaging: Image Processing, vol. 3661, pp. 716–727 Sometimes, more than one of these advantages compound together, thereby increasing the efficiency by 50% in terms of computation and storage when compared to rectangular sampling. Despite all of these advantages of hexagonal sampling over rectangular sampling, its application has been limited because of the lack of an efficient coordinate system.Nicholas I. Rummelt and Joseph N. Wilson "Array set addressing: enabling technology for the efficient processing of hexagonally sampled imagery," Journal of Electronic Imaging 20(2), 023012 (1 April 2011). https://doi.org/10.1117/1.3589306 However that limitation has been removed with the recent development of the hexagonal efficient coordinate system (HECS, formerly known as array set addressing or ASA) which includes the benefit of a separable Fourier kernel. The existence of a separable Fourier kernel for a hexagonally sampled image allows the use of existing FFT routines to efficiently compute the DFT of such an image.
Preliminaries
Hexagonal Efficient Coordinate System (HECS)
 The hexagonal efficient coordinate system (formerly known as array set addressing (ASA)) was developed based on the fact that a hexagonal grid can be represented as a combination of two interleaved rectangular arrays.Nicholas I. Rummelt, 2010, Array Set Addressing: Enabling Efficient Hexagonally Sampled Image Processing, Ph.D. thesis, University of Florida It is easy to address each individual array using familiar integer-valued row and column indices and the individual arrays are distinguished by a single binary coordinate. Therefore, a full address for any point in the hexagonal grid can be uniquely represented by three coordinates.
::
where the coordinates ''a'', ''r'' and ''c'' represent the array, row and column respectively. The figure shows how the hexagonal grid is represented by two interleaved rectangular arrays in HECS coordinates.
The hexagonal efficient coordinate system (formerly known as array set addressing (ASA)) was developed based on the fact that a hexagonal grid can be represented as a combination of two interleaved rectangular arrays.Nicholas I. Rummelt, 2010, Array Set Addressing: Enabling Efficient Hexagonally Sampled Image Processing, Ph.D. thesis, University of Florida It is easy to address each individual array using familiar integer-valued row and column indices and the individual arrays are distinguished by a single binary coordinate. Therefore, a full address for any point in the hexagonal grid can be uniquely represented by three coordinates.
::
where the coordinates ''a'', ''r'' and ''c'' represent the array, row and column respectively. The figure shows how the hexagonal grid is represented by two interleaved rectangular arrays in HECS coordinates.
Hexagonal discrete Fourier transform
The hexagonal discrete Fourier transform (HDFT) has been developed by Mersereau and it has been converted to an HECS representation by Rummelt. Let be a two-dimensional hexagonally sampled signal and let both arrays be of size . Let, be theFourier transform
In mathematics, the Fourier transform (FT) is an integral transform that takes a function as input then outputs another function that describes the extent to which various frequencies are present in the original function. The output of the tr ...
of ''x.'' The HDFT equation for the forward transform as shown in is given by
::
where
::