Hesse normal form on:
[Wikipedia]
[Google]
[Amazon]
 In
In
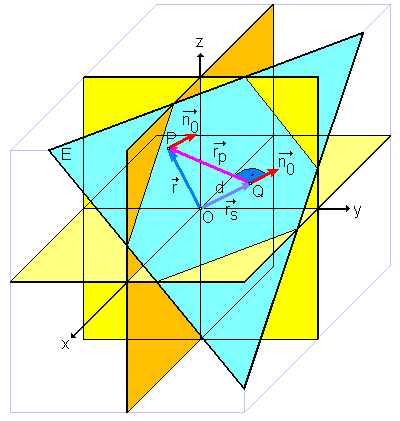 In this diagram, ''d'' is the distance from the origin. Because holds for every point in the plane, it is also true at point ''Q'' (the point where the vector from the origin meets the plane E), with , per the definition of the
In this diagram, ''d'' is the distance from the origin. Because holds for every point in the plane, it is also true at point ''Q'' (the point where the vector from the origin meets the plane E), with , per the definition of the
analytic geometry
In mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.
Analytic geometry is used in physics and engineering, and als ...
, the Hesse normal form (named after Otto Hesse) is an equation used to describe a line in the Euclidean plane
In mathematics, a Euclidean plane is a Euclidean space of Two-dimensional space, dimension two, denoted \textbf^2 or \mathbb^2. It is a geometric space in which two real numbers are required to determine the position (geometry), position of eac ...
, a plane in Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
, or a hyperplane
In geometry, a hyperplane is a generalization of a two-dimensional plane in three-dimensional space to mathematical spaces of arbitrary dimension. Like a plane in space, a hyperplane is a flat hypersurface, a subspace whose dimension is ...
in higher dimension
In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coo ...
s.John Vince: ''Geometry for Computer Graphics''. Springer, 2005, , pp. 42, 58, 135, 273 It is primarily used for calculating distances (see point-plane distance and point-line distance).
It is written in vector notation as
:
The dot indicates the dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a Scalar (mathematics), scalar as a result". It is also used for other symmetric bilinear forms, for example in a pseudo-Euclidean space. N ...
(or scalar product).
Vector points from the origin of the coordinate system, ''O'', to any point ''P'' that lies precisely in plane or on line ''E''. The vector represents the unit normal vector
In geometry, a normal is an object (e.g. a line, ray, or vector) that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the infinite straight line perpendicular to the tangent line to the cu ...
of plane or line ''E''. The distance is the shortest distance from the origin ''O'' to the plane or line.
Derivation/Calculation from the normal form
Note: For simplicity, the following derivation discusses the 3D case. However, it is also applicable in 2D. In the normal form, : a plane is given by a normal vector as well as an arbitrary position vector of a point . The direction of is chosen to satisfy the following inequality : By dividing the normal vector by itsmagnitude
Magnitude may refer to:
Mathematics
*Euclidean vector, a quantity defined by both its magnitude and its direction
*Magnitude (mathematics), the relative size of an object
*Norm (mathematics), a term for the size or length of a vector
*Order of ...
, we obtain the unit (or normalized) normal vector
:
and the above equation can be rewritten as
:
Substituting
:
we obtain the Hesse normal form
:
Scalar product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a scalar as a result". It is also used for other symmetric bilinear forms, for example in a pseudo-Euclidean space. Not to be confused wit ...
:
The magnitude of is the shortest distance from the origin to the plane.
Distance to a line
The Quadrance (distance squared) from a line to a point is : If has unit length then this becomesReferences
External links
*{{MathWorld, title=Hessian Normal Form, urlname=HessianNormalForm Analytic geometry