Harmonic analysis

Harmonic analysis is a branch of mathematics concerned with the representation of functions or signals as the superposition of basic waves, and the study of and generalization of the notions of Fourier series and Fourier transforms (i.e. an extended form of Fourier analysis). In the past two centuries, it has become a vast subject with applications in areas as diverse as number theory, representation theory, signal processing, quantum mechanics, tidal analysis and neuroscience.

The term " harmonics" originated as the Ancient Greek word ''harmonikos'', meaning "skilled in music". In physical eigenvalue problems, it began to mean waves whose frequencies are integer multiples of one another, as are the frequencies of the harmonics of music notes, but the term has been generalized beyond its original meaning.

The classical Fourier transform on R^''n'' is still an area of ongoing research, particularly concerning Fourier transformation on more general objects such as tempered distributions. For instance, if we impose some requirements on a distribution ''f'', we can attempt to translate these requirements in terms of the Fourier transform of ''f''. The Paley–Wiener theorem is an example of this. The Paley–Wiener theorem immediately implies that if ''f'' is a nonzero distribution of compact support (these include functions of compact support), then its Fourier transform is never compactly supported (i.e. if a signal is limited in one domain, it is unlimited in the other). This is a very elementary form of an uncertainty principle in a harmonic-analysis setting.

Fourier series can be conveniently studied in the context of Hilbert spaces, which provides a connection between harmonic analysis and functional analysis. There are four versions of the Fourier transform, dependent on the spaces that are mapped by the transformation (discrete/periodic–discrete/periodic: discrete Fourier transform, continuous/periodic–discrete/aperiodic: Fourier series, discrete/aperiodic–continuous/periodic: discrete-time Fourier transform, continuous/aperiodic–continuous/aperiodic: Fourier transform).

Abstract harmonic analysis

One of the most modern branches of harmonic analysis, having its roots in the mid-20th century, is analysis on topological groups. The core motivating ideas are the various Fourier transforms, which can be generalized to a transform of functions defined on Hausdorff locally compact topological groups.

The theory for abelian locally compact groups is called Pontryagin duality.

Harmonic analysis studies the properties of that duality and Fourier transform and attempts to extend those features to different settings, for instance, to the case of non-abelian Lie groups.

For general non-abelian locally compact groups, harmonic analysis is closely related to the theory of unitary group representations. For compact groups, the Peter–Weyl theorem explains how one may get harmonics by choosing one irreducible representation out of each equivalence class of representations. This choice of harmonics enjoys some of the useful properties of the classical Fourier transform in terms of carrying convolutions to pointwise products, or otherwise showing a certain understanding of the underlying group structure. See also: Non-commutative harmonic analysis.

If the group is neither abelian nor compact, no general satisfactory theory is currently known ("satisfactory" means at least as strong as the Plancherel theorem). However, many specific cases have been analyzed, for example SL_''n''. In this case, representations in infinite dimensions play a crucial role.

Other branches

*Study of the eigenvalues and eigenvectors of the Laplacian on domains, manifolds, and (to a lesser extent) graphs is also considered a branch of harmonic analysis. See e.g., hearing the shape of a drum.
* Harmonic analysis on Euclidean spaces deals with properties of the Fourier transform on R^''n'' that have no analog on general groups. For example, the fact that the Fourier transform is rotation-invariant. Decomposing the Fourier transform into its radial and spherical components leads to topics such as Bessel functions and spherical harmonics.
* Harmonic analysis on tube domains is concerned with generalizing properties of Hardy spaces to higher dimensions.

Applied harmonic analysis

Many applications of harmonic analysis in science and engineering begin with the idea or hypothesis that a phenomenon or signal is composed of a sum of individual oscillatory components. Ocean tides and vibrating strings are common and simple examples. The theoretical approach is often to try to describe the system by a differential equation or system of equations to predict the essential features, including the amplitude, frequency, and phases of the oscillatory components. The specific equations depend on the field, but theories generally try to select equations that represent major principles that are applicable.

The experimental approach is usually to acquire data that accurately quantifies the phenomenon. For example, in a study of tides, the experimentalist would acquire samples of water depth as a function of time at closely enough spaced intervals to see each oscillation and over a long enough duration that multiple oscillatory periods are likely included. In a study on vibrating strings, it is common for the experimentalist to acquire a sound waveform sampled at a rate at least twice that of the highest frequency expected and for a duration many times the period of the lowest frequency expected.

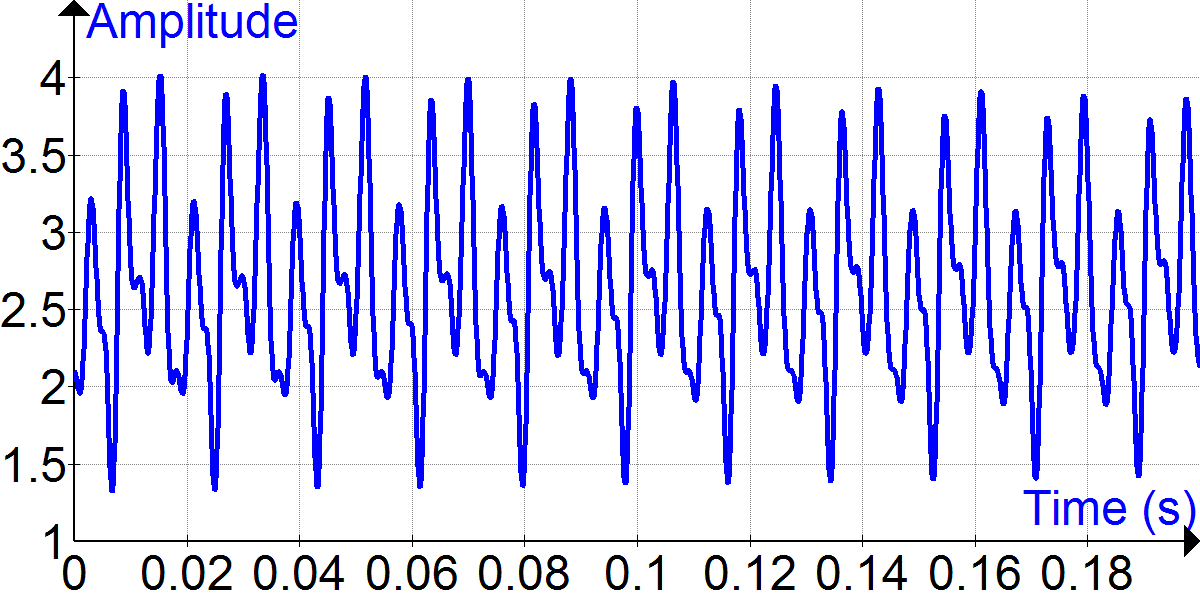
For example, the top signal at the right is a sound waveform of a bass guitar playing an open string corresponding to an A note with a fundamental frequency of 55 Hz. The waveform appears oscillatory, but it is more complex than a simple sine wave, indicating the presence of additional waves. The different wave components contributing to the sound can be revealed by applying a mathematical analysis technique known as the Fourier transform, the result of which is shown in the lower figure. Note that there is a prominent peak at 55 Hz, but that there are other peaks at 110 Hz, 165 Hz, and at other frequencies corresponding to integer multiples of 55 Hz. In this case, 55 Hz is identified as the fundamental frequency of the string vibration, and the integer multiples are known as harmonics.

See also

* Convergence of Fourier series
* Fourier analysis for computing periodicity in evenly spaced data
* Harmonic (mathematics)
* Least-squares spectral analysis for computing periodicity in unevenly spaced data
* Spectral density estimation
* Tate's thesis

References

Bibliography

* Elias Stein and Guido Weiss, ''Introduction to Fourier Analysis on Euclidean Spaces'', Princeton University Press, 1971.
* Elias Stein with Timothy S. Murphy, ''Harmonic Analysis: Real-Variable Methods, Orthogonality, and Oscillatory Integrals'', Princeton University Press, 1993.
* Elias Stein, ''Topics in Harmonic Analysis Related to the Littlewood-Paley Theory'', Princeton University Press, 1970.
*Yitzhak Katznelson, ''An introduction to harmonic analysis'', Third edition. Cambridge University Press, 2004. ; 0-521-54359-2
* Terence Tao
Fourier Transform
(Introduces the decomposition of functions into odd + even parts as a harmonic decomposition over ℤ₂.)
* Yurii I. Lyubich. ''Introduction to the Theory of Banach Representations of Groups''. Translated from the 1985 Russian-language edition (Kharkov, Ukraine). Birkhäuser Verlag. 1988.
* George W. Mackey
Harmonic analysis as the exploitation of symmetry–a historical survey
''Bull. Amer. Math. Soc.'' 3 (1980), 543–698.
* M. Bujosa, A. Bujosa and A. Garcıa-Ferrer
Mathematical Framework for Pseudo-Spectra of Linear Stochastic Difference Equations
''IEEE Transactions on Signal Processing'' vol. 63 (2015), 6498-6509.

External links

{{Authority control

Acoustics

Musical terminology