Green's Function

In mathematics, a Green's function is the impulse response of an inhomogeneous linear differential operator defined on a domain with specified initial conditions or boundary conditions.

This means that if $\operatorname$ is the linear differential operator, then

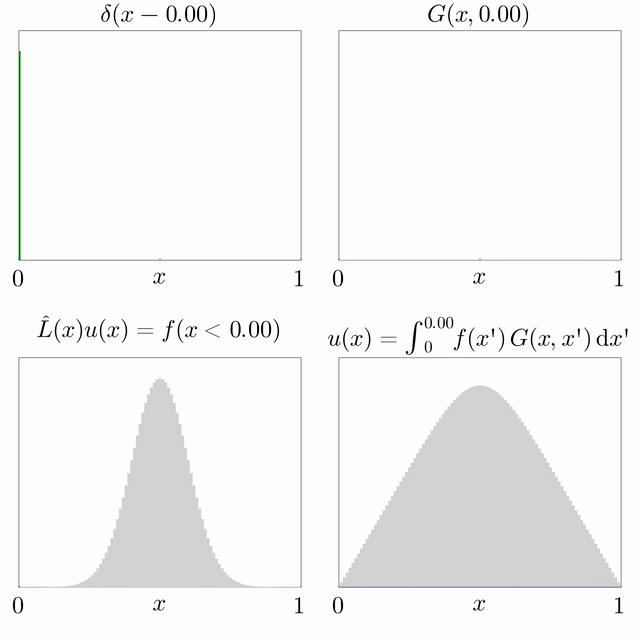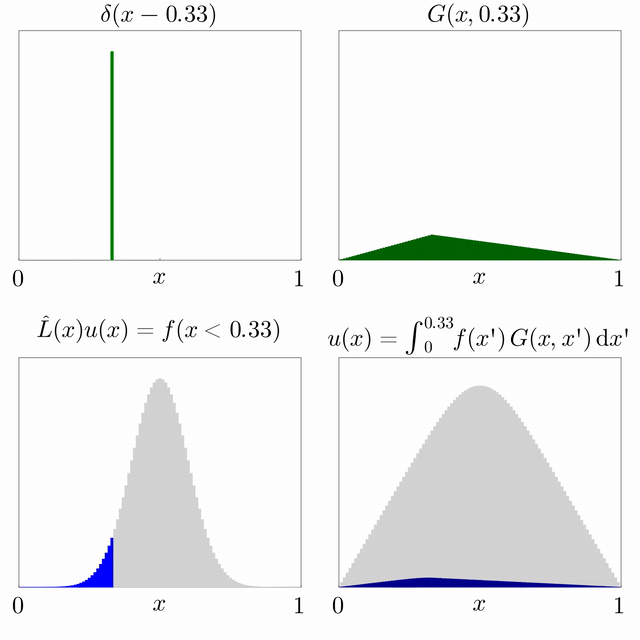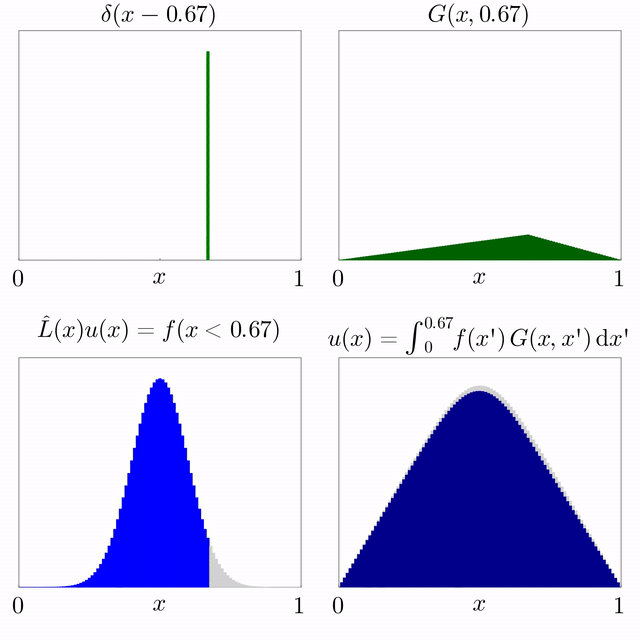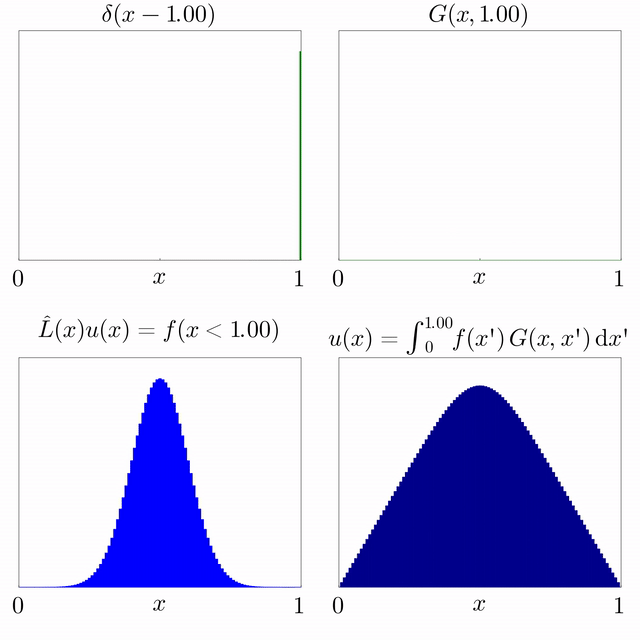
* the Green's function $G$ is the solution of the equation $\operatorname G = \delta$, where $\delta$ is Dirac's delta function;
* the solution of the initial-value problem $\operatorname y = f$ is the convolution ($G \ast f$).

Through the superposition principle, given a linear ordinary differential equation (ODE), $\operatorname y = f$, one can first solve $\operatorname G = \delta_s$, for each , and realizing that, since the source is a sum of delta functions, the solution is a sum of Green's functions as well, by linearity of .

Green's functions are named after the British mathematician George Green, who first developed the concept in the 1820s. In the modern study of linear partial differential equations, Green's functions are studied largely from the point of view of fundamental solutions instead.

Under many-body theory, the term is also used in physics, specifically in quantum field theory, aerodynamics, aeroacoustics, electrodynamics, seismology and statistical field theory, to refer to various types of correlation functions, even those that do not fit the mathematical definition. In quantum field theory, Green's functions take the roles of propagators.

Definition and uses

A Green's function, , of a linear differential operator $\operatorname = \operatorname(x)$ acting on distributions over a subset of the Euclidean space $\R^n$, at a point , is any solution of

where is the Dirac delta function. This property of a Green's function can be exploited to solve differential equations of the form

If the kernel of is non-trivial, then the Green's function is not unique. However, in practice, some combination of symmetry, boundary conditions and/or other externally imposed criteria will give a unique Green's function. Green's functions may be categorized, by the type of boundary conditions satisfied, by a Green's function number. Also, Green's functions in general are distributions, not necessarily functions of a real variable.

Green's functions are also useful tools in solving wave equations and diffusion equations. In quantum mechanics, Green's function of the Hamiltonian is a key concept with important links to the concept of density of states.

The Green's function as used in physics is usually defined with the opposite sign, instead. That is,
$\operatorname \, G(x,s) = \delta(x-s)~.$
This definition does not significantly change any of the properties of Green's function due to the evenness of the Dirac delta function.

If the operator is translation invariant, that is, when $\operatorname$ has constant coefficients with respect to , then the Green's function can be taken to be a convolution kernel, that is,
$G(x,s) = G(x-s)~.$

In this case, Green's function is the same as the impulse response of linear time-invariant system theory.

Motivation

Loosely speaking, if such a function can be found for the operator $\operatorname$, then, if we multiply the equation () for the Green's function by , and then integrate with respect to , we obtain,
$\int \operatorname\,G(x,s)\,f(s) \, ds = \int \delta(x-s) \, f(s) \, ds = f(x)~.$

Because the operator $\operatorname = \operatorname(x)$ is linear and acts only on the variable (and ''not'' on the variable of integration ), one may take the operator $\operatorname$ outside of the integration, yielding
$\operatorname\,\left(\int G(x,s)\,f(s) \,ds \right) = f(x)~.$
This means that

is a solution to the equation $\operatorname u(x) = f(x)~.$

Thus, one may obtain the function through knowledge of the Green's function in equation () and the source term on the right-hand side in equation (). This process relies upon the linearity of the operator $\operatorname$.

In other words, the solution of equation (), , can be determined by the integration given in equation (). Although is known, this integration cannot be performed unless is also known. The problem now lies in finding the Green's function that satisfies equation (). For this reason, the Green's function is also sometimes called the fundamental solution associated to the operator $\operatorname$.

Not every operator $\operatorname$ admits a Green's function. A Green's function can also be thought of as a right inverse of $\operatorname$. Aside from the difficulties of finding a Green's function for a particular operator, the integral in equation () may be quite difficult to evaluate. However the method gives a theoretically exact result.

This can be thought of as an expansion of according to a Dirac delta function basis (projecting over $\delta(x - s)$; and a superposition of the solution on each projection. Such an integral equation is known as a Fredholm integral equation, the study of which constitutes Fredholm theory.

Green's functions for solving inhomogeneous boundary value problems

The primary use of Green's functions in mathematics is to solve non-homogeneous boundary value problems. In modern theoretical physics, Green's functions are also usually used as propagators in Feynman diagrams; the term ''Green's function'' is often further used for any correlation function.

Framework

Let $\operatorname$ be the Sturm–Liouville operator, a linear differential operator of the form
\operatorname=\dfrac\left (x) \dfrac\rightq(x)
and let $\vec\operatorname$ be the vector-valued boundary conditions operator
$\vec\operatorname\,u= \begin \alpha_1 u'(0)+\beta_1 u(0) \\ \alpha_2 u'(\ell)+\beta_2 u(\ell) \end ~.$

Let $f(x)$ be a continuous function in ,\ell,. Further suppose that the problem
$\begin \operatorname\,u &= f \\ \vec\operatorname\,u &= \vec \end$
is "regular", i.e., the only solution for $f(x) = 0$ for all is $u(x) = 0$.

Theorem

There is one and only one solution $u(x)$ that satisfies
$\begin \operatorname\,u & = f\\ \vec\operatorname\,u & = \vec \end$
and it is given by
$u(x)=\int_0^\ell f(s) \, G(x,s) \, ds~,$
where $G(x,s)$ is a Green's function satisfying the following conditions:
# $G(x,s)$ is continuous in $x$ and $s$.
# For $x \ne s~$, $\quad \operatorname\,G(x,s) = 0~$.
# For $s \ne 0~$, $\quad \vec\operatorname\,G(x,s) = \vec~$.
# Derivative "jump": $\quad G'(s_,s) - G'(s_,s) = 1 / p(s)~$.
# Symmetry: $\quad G(x,s) = G(s,x)~$.

Advanced and retarded Green's functions

Green's function is not necessarily unique since the addition of any solution of the homogeneous equation to one Green's function results in another Green's function. Therefore if the homogeneous equation has nontrivial solutions, multiple Green's functions exist. In some cases, it is possible to find one Green's function that is nonvanishing only for $s \leq x$, which is called a retarded Green's function, and another Green's function that is nonvanishing only for $s \geq x$, which is called an advanced Green's function. In such cases, any linear combination of the two Green's functions is also a valid Green's function. The terminology advanced and retarded is especially useful when the variable x corresponds to time. In such cases, the solution provided by the use of the retarded Green's function depends only on the past sources and is causal whereas the solution provided by the use of the advanced Green's function depends only on the future sources and is acausal. In these problems, it is often the case that the causal solution is the physically important one. The use of advanced and retarded Green's function is especially common for the analysis of solutions of the inhomogeneous electromagnetic wave equation.

Finding Green's functions

Units

While it doesn't uniquely fix the form the Green's function will take, performing a dimensional analysis to find the units a Green's function must have is an important sanity check on any Green's function found through other means. A quick examination of the defining equation,
$L G(x, s) = \delta(x - s),$
shows that the units of $G$ depend not only on the units of $L$ but also on the number and units of the space of which the position vectors $x$ and $s$ are elements. This leads to the relationship:
G = L^ d x^,
where G is defined as, "the physical units of $G$", and $d x$ is the volume element of the space (or spacetime).

For example, if $L = \partial_t^2$ and time is the only variable then:
L = \text^,
d x = \text,\ \text
G = \text.
If $L = \square = \frac\partial_t^2-\nabla^2$, the d'Alembert operator, and space has 3 dimensions then:
L = \text^,
dx = \text \text^3,\ \text
G = \text^ \text^.

Eigenvalue expansions

If a differential operator admits a set of eigenvectors (i.e., a set of functions and scalars such that ) that is complete, then it is possible to construct a Green's function from these eigenvectors and eigenvalues.

"Complete" means that the set of functions satisfies the following completeness relation,
$\delta(x-x') = \sum_^\infty \Psi_n^\dagger(x) \Psi_n(x').$

Then the following holds,

where $\dagger$ represents complex conjugation.

Applying the operator to each side of this equation results in the completeness relation, which was assumed.

The general study of Green's function written in the above form, and its relationship to the function spaces formed by the eigenvectors, is known as Fredholm theory.

There are several other methods for finding Green's functions, including the method of images, separation of variables, and Laplace transforms.

Combining Green's functions

If the differential operator $L$ can be factored as $L = L_1 L_2$ then the Green's function of $L$ can be constructed from the Green's functions for $L_1$ and $L_2$:
$G(x, s) = \int G_2(x, s_1)\, G_1(s_1, s) \, d s_1.$
The above identity follows immediately from taking $G(x, s)$ to be the representation of the right operator inverse of $L$, analogous to how for the invertible linear operator $C$, defined by $C = (AB)^ = B^ A^$, is represented by its matrix elements $C_$.

A further identity follows for differential operators that are scalar polynomials of the derivative, $L = P_N(\partial_x)$. The fundamental theorem of algebra, combined with the fact that $\partial_x$ commutes with itself, guarantees that the polynomial can be factored, putting $L$ in the form:
$L = \prod_^N (\partial_x - z_i),$
where $z_i$ are the zeros of $P_N(z)$. Taking the Fourier transform of $L G(x, s) = \delta(x - s)$ with respect to both $x$ and $s$ gives:
$\widehat(k_x, k_s) = \frac.$
The fraction can then be split into a sum using a partial fraction decomposition before Fourier transforming back to $x$ and $s$ space. This process yields identities that relate integrals of Green's functions and sums of the same. For example, if $L = (\partial_x + \gamma) (\partial_x + \alpha)^2$ then one form for its Green's function is:
\begin
G(x, s) & = \frac\Theta(x-s) e^ - \frac\Theta(x-s) e^ + \frac \Theta(x - s) \, (x - s) e^ \\ pt& = \int \Theta(x - s_1) (x - s_1) e^ \Theta(s_1 - s) e^ \, ds_1.
\end
While the example presented is tractable analytically, it illustrates a process that works when the integral is not trivial (for example, when $\nabla^2$ is the operator in the polynomial).

Table of Green's functions

The following table gives an overview of Green's functions of frequently appearing differential operators, where $r = \sqrt$, $\rho = \sqrt$, $\Theta(t)$ is the Heaviside step function, $J_\nu(z)$ is a Bessel function, $I_\nu(z)$ is a modified Bessel function of the first kind, and $K_\nu(z)$ is a modified Bessel function of the second kind. Where time () appears in the first column, the retarded (causal) Green's function is listed.

Green's functions for the Laplacian

Green's functions for linear differential operators involving the Laplacian may be readily put to use using the second of Green's identities.

To derive Green's theorem, begin with the divergence theorem (otherwise known as Gauss's theorem),
$\int_V \nabla \cdot \vec A\ dV=\int_S \vec A \cdot d\widehat\sigma ~.$

Let $\vec A=\varphi\,\nabla\psi-\psi\,\nabla\varphi$ and substitute into Gauss' law.

Compute $\nabla\cdot\vec A$ and apply the product rule for the ∇ operator,
$\begin \nabla\cdot\vec A &=\nabla\cdot(\varphi\,\nabla\psi \;-\; \psi\,\nabla\varphi)\\ &=(\nabla\varphi)\cdot(\nabla\psi) \;+\; \varphi\,\nabla^2\psi \;-\; (\nabla\varphi)\cdot(\nabla\psi) \;-\; \psi\nabla^2\varphi\\ &=\varphi\,\nabla^2\psi \;-\; \psi\,\nabla^2\varphi. \end$

Plugging this into the divergence theorem produces Green's theorem,
$\int_V (\varphi\,\nabla^2\psi-\psi\,\nabla^2\varphi) \, dV = \int_S (\varphi\,\nabla\psi-\psi\nabla\,\varphi)\cdot d\widehat\sigma.$

Suppose that the linear differential operator is the Laplacian, ∇², and that there is a Green's function for the Laplacian. The defining property of the Green's function still holds,
$L G(x,x')=\nabla^2 G(x,x')=\delta(x-x').$

Let $\psi=G$ in Green's second identity, see Green's identities. Then,
\int_V \left \varphi(x') \delta(x-x')-G(x,x') \, ^2\,\varphi(x')\right d^3x' = \int_S \left varphi(x')\, G(x,x')-G(x,x')\,\varphi(x')\right\cdot d\widehat\sigma'.

Using this expression, it is possible to solve Laplace's equation ∇²''φ''(''x'') = 0 or Poisson's equation ∇²''φ''(''x'') = −''ρ''(''x''), subject to either Neumann or Dirichlet boundary conditions. In other words, we can solve for ''φ''(''x'') everywhere inside a volume where either (1) the value of ''φ''(''x'') is specified on the bounding surface of the volume (Dirichlet boundary conditions), or (2) the normal derivative of ''φ''(''x'') is specified on the bounding surface (Neumann boundary conditions).

Suppose the problem is to solve for ''φ''(''x'') inside the region. Then the integral
$\int_V \varphi(x')\delta(x-x')\, d^3x'$
reduces to simply ''φ''(''x'') due to the defining property of the Dirac delta function and we have
\varphi(x) = -\int_V G(x,x') \rho(x')\ d^3x' + \int_S \left varphi(x') \, \nabla' G(x,x')-G(x,x') \,\nabla'\varphi(x')\right\cdot d\widehat\sigma'.

This form expresses the well-known property of harmonic functions, that ''if the value or normal derivative is known on a bounding surface, then the value of the function inside the volume is known everywhere''.

In electrostatics, ''φ''(''x'') is interpreted as the electric potential, ''ρ''(''x'') as electric charge density, and the normal derivative $\nabla\varphi(x')\cdot d\widehat\sigma'$ as the normal component of the electric field.

If the problem is to solve a Dirichlet boundary value problem, the Green's function should be chosen such that ''G''(''x'',''x''′) vanishes when either ''x'' or ''x''′ is on the bounding surface. Thus only one of the two terms in the surface integral remains. If the problem is to solve a Neumann boundary value problem, it might seem logical to choose Green's function so that its normal derivative vanishes on the bounding surface. However, application of Gauss's theorem to the differential equation defining the Green's function yields
$\int_S \nabla' G(x,x') \cdot d\widehat\sigma' = \int_V \nabla'^2 G(x,x') d^3x' = \int_V \delta (x-x') d^3x' = 1 ~,$
meaning the normal derivative of ''G''(''x'',''x''′) cannot vanish on the surface, because it must integrate to 1 on the surface.

The simplest form the normal derivative can take is that of a constant, namely 1/''S'', where ''S'' is the surface area of the surface. The surface term in the solution becomes
$\int_S \varphi(x') \, \nabla' G(x,x')\cdot d\widehat\sigma' = \langle\varphi\rangle_S$
where $\langle\varphi\rangle_S$ is the average value of the potential on the surface. This number is not known in general, but is often unimportant, as the goal is often to obtain the electric field given by the gradient of the potential, rather than the potential itself.

With no boundary conditions, the Green's function for the Laplacian (Green's function for the three-variable Laplace equation) is
$G(x,x')=-\dfrac.$

Supposing that the bounding surface goes out to infinity and plugging in this expression for the Green's function finally yields the standard expression for electric potential in terms of electric charge density as

Example

Find the Green function for the following problem, whose Green's function number is X11:

$\begin Lu & = u'' + k^2 u = f(x)\\ u(0)& = 0, \quad u\left(\tfrac\right) = 0. \end$

First step: The Green's function for the linear operator at hand is defined as the solution to

If $x\ne s$, then the delta function gives zero, and the general solution is

$G(x,s)=c_1 \cos kx+c_2 \sin kx.$

For x, the boundary condition at $x=0$ implies

$G(0,s)=c_1 \cdot 1+c_2 \cdot 0=0, \quad c_1 = 0$

if $x < s$ and $s \ne \tfrac$.

For $x>s$, the boundary condition at $x=\tfrac$ implies

$G\left(\tfrac,s\right) = c_3 \cdot 0+c_4 \cdot 1=0, \quad c_4 = 0$

The equation of $G(0,s)=0$ is skipped for similar reasons.

To summarize the results thus far:

G(x,s)= \begin
c_2 \sin kx, & \textx

Second step: The next task is to determine $c_2$ and $c_3$.

Ensuring continuity in the Green's function at $x=s$ implies

$c_2 \sin ks=c_3 \cos ks$

One can ensure proper discontinuity in the first derivative by integrating the defining differential equation (i.e., ) from $x=s-\varepsilon$ to $x=s+\varepsilon$ and taking the limit as $\varepsilon$ goes to zero. Note that we only integrate the second derivative as the remaining term will be continuous by construction.

$c_3 \cdot (-k \sin ks)-c_2 \cdot (k \cos ks)=1$

The two (dis)continuity equations can be solved for $c_2$ and $c_3$ to obtain

$c_2 = -\frac \quad;\quad c_3 = -\frac$

So Green's function for this problem is:

G(x,s)=\begin
-\frac \sin kx, & x

Further examples

* Let and let the subset be all of R. Let be $\frac$. Then, the Heaviside step function is a Green's function of at .
* Let and let the subset be the quarter-plane and be the Laplacian. Also, assume a Dirichlet boundary condition is imposed at and a Neumann boundary condition is imposed at . Then the X10Y20 Green's function is \begin
G(x, y, x_0, y_0) =\dfrac &\left pt&\left.__+_\ln\sqrt-_\ln\sqrt_\,_\right.html" ;"title="ln\sqrt-\ln\sqrt \right. \\ pt&\left. + \ln\sqrt- \ln\sqrt \, \right">ln\sqrt-\ln\sqrt \right. \\ pt&\left. + \ln\sqrt- \ln\sqrt \, \right
\end
* Let $a < x < b$, and all three are elements of the real numbers. Then, for any function $f:\mathbb\to\mathbb$ with an $n$-th derivative that is integrable over the interval , b/math>: \begin
f(x) & = \sum_^ \frac \left \frac \right + \int_a^b \left frac \Theta(x - s)\right\left \frac \right ds
\end ~. The Green's function in the above equation, $G(x,s) = \frac \Theta(x - s)$, is not unique. How is the equation modified if $g(x-s)$ is added to $G(x,s)$, where $g(x)$ satisfies $\frac = 0$ for all x \in , b/math> (for example, $g(x) = -x/2$ with Also, compare the above equation to the form of a Taylor series centered at $x = a$.

See also

* Bessel potential
* Discrete Green's functions – defined on graphs and grids
* Impulse response – the analog of a Green's function in signal processing
* Transfer function
* Fundamental solution
* Green's function in many-body theory
* Correlation function
* Propagator
* Green's identities
* Parametrix
* Volterra integral equation
* Resolvent formalism
* Keldysh formalism
* Spectral theory
* Multiscale Green's function

Footnotes

References

*
*
''Chapter 5 contains a very readable account of using Green's functions to solve boundary value problems in electrostatics.''
*
*
*
*
*
*
*

External links

*
*
*
*
*

Introduction to the Keldysh Nonequilibrium Green Function Technique
by A. P. Jauho






* ttp://en.citizendium.org/wiki/Green%27s_function At Citizendium* ttps://archive.today/20130101181958/http://academicearth.com/lectures/delta-function-and-greens-function MIT video lecture on Green's function*

{{Authority control

Differential equations
Generalized functions
Equations of physics
Mathematical physics