Gaussian channel on:
[Wikipedia]
[Google]
[Amazon]
Additive white Gaussian noise (AWGN) is a basic noise model used in
 In serial data communications, the AWGN mathematical model is used to model the timing error caused by random jitter (RJ).
The graph to the right shows an example of timing errors associated with AWGN. The variable Δ''t'' represents the uncertainty in the zero crossing. As the amplitude of the AWGN is increased, the signal-to-noise ratio decreases. This results in increased uncertainty Δ''t''.
When affected by AWGN, the average number of either positive-going or negative-going zero crossings per second at the output of a narrow bandpass filter when the input is a sine wave is
:
:
where
: ''f''0 = the center frequency of the filter,
: ''B'' = the filter bandwidth,
: SNR = the signal-to-noise power ratio in linear terms.
In serial data communications, the AWGN mathematical model is used to model the timing error caused by random jitter (RJ).
The graph to the right shows an example of timing errors associated with AWGN. The variable Δ''t'' represents the uncertainty in the zero crossing. As the amplitude of the AWGN is increased, the signal-to-noise ratio decreases. This results in increased uncertainty Δ''t''.
When affected by AWGN, the average number of either positive-going or negative-going zero crossings per second at the output of a narrow bandpass filter when the input is a sine wave is
:
:
where
: ''f''0 = the center frequency of the filter,
: ''B'' = the filter bandwidth,
: SNR = the signal-to-noise power ratio in linear terms.
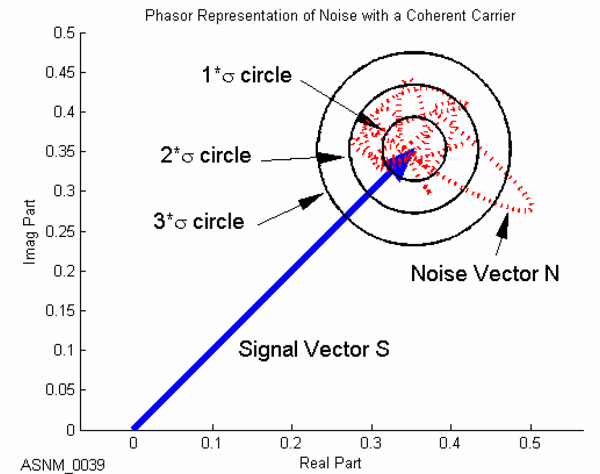 In modern communication systems, bandlimited AWGN cannot be ignored. When modeling bandlimited AWGN in the phasor domain, statistical analysis reveals that the amplitudes of the real and imaginary contributions are independent variables which follow the
In modern communication systems, bandlimited AWGN cannot be ignored. When modeling bandlimited AWGN in the phasor domain, statistical analysis reveals that the amplitudes of the real and imaginary contributions are independent variables which follow the
information theory
Information theory is the scientific study of the quantification, storage, and communication of information. The field was originally established by the works of Harry Nyquist and Ralph Hartley, in the 1920s, and Claude Shannon in the 1940s. ...
to mimic the effect of many random processes that occur in nature. The modifiers denote specific characteristics:
* ''Additive'' because it is added to any noise that might be intrinsic to the information system.
* ''White'' refers to the idea that it has uniform power across the frequency band for the information system. It is an analogy to the color white which has uniform emissions at all frequencies in the visible spectrum
The visible spectrum is the portion of the electromagnetic spectrum that is visible to the human eye. Electromagnetic radiation in this range of wavelengths is called '' visible light'' or simply light. A typical human eye will respond to ...
.
* ''Gaussian'' because it has a normal distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is
:
f(x) = \frac e^
The parameter \mu ...
in the time domain with an average time domain value of zero.
Wideband noise comes from many natural noise sources, such as the thermal vibrations of atoms in conductors (referred to as thermal noise or Johnson–Nyquist noise
Johnson–Nyquist noise (thermal noise, Johnson noise, or Nyquist noise) is the electronic noise generated by the thermal agitation of the charge carriers (usually the electrons) inside an electrical conductor at equilibrium, which happens reg ...
), shot noise
Shot noise or Poisson noise is a type of noise which can be modeled by a Poisson process.
In electronics shot noise originates from the discrete nature of electric charge. Shot noise also occurs in photon counting in optical devices, where sh ...
, black-body radiation
Black-body radiation is the thermal electromagnetic radiation within, or surrounding, a body in thermodynamic equilibrium with its environment, emitted by a black body (an idealized opaque, non-reflective body). It has a specific, continuous spe ...
from the earth and other warm objects, and from celestial sources such as the Sun. The central limit theorem
In probability theory, the central limit theorem (CLT) establishes that, in many situations, when independent random variables are summed up, their properly normalized sum tends toward a normal distribution even if the original variables themsel ...
of probability theory
Probability theory is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set ...
indicates that the summation of many random processes will tend to have distribution called Gaussian or Normal.
AWGN is often used as a channel model
A communication channel refers either to a physical transmission medium such as a wire, or to a logical connection over a multiplexed medium such as a radio channel in telecommunications and computer networking. A channel is used for info ...
in which the only impairment to communication is a linear addition of wideband
In communications, a system is wideband when the message bandwidth significantly exceeds the coherence bandwidth of the channel. Some communication links have such a high data rate that they are forced to use a wide bandwidth; other links ma ...
or white noise
In signal processing, white noise is a random signal having equal intensity at different frequencies, giving it a constant power spectral density. The term is used, with this or similar meanings, in many scientific and technical disciplines ...
with a constant spectral density
The power spectrum S_(f) of a time series x(t) describes the distribution of power into frequency components composing that signal. According to Fourier analysis, any physical signal can be decomposed into a number of discrete frequencies ...
(expressed as watt
The watt (symbol: W) is the unit of power or radiant flux in the International System of Units (SI), equal to 1 joule per second or 1 kg⋅m2⋅s−3. It is used to quantify the rate of energy transfer. The watt is named after James ...
s per hertz
The hertz (symbol: Hz) is the unit of frequency in the International System of Units (SI), equivalent to one event (or cycle) per second. The hertz is an SI derived unit whose expression in terms of SI base units is s−1, meaning that o ...
of bandwidth) and a Gaussian distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is
:
f(x) = \frac e^
The parameter \mu ...
of amplitude. The model does not account for fading, frequency
Frequency is the number of occurrences of a repeating event per unit of time. It is also occasionally referred to as ''temporal frequency'' for clarity, and is distinct from ''angular frequency''. Frequency is measured in hertz (Hz) which is eq ...
selectivity, interference
Interference is the act of interfering, invading, or poaching. Interference may also refer to:
Communications
* Interference (communication), anything which alters, modifies, or disrupts a message
* Adjacent-channel interference, caused by extr ...
, nonlinearity
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other ...
or dispersion
Dispersion may refer to:
Economics and finance
* Dispersion (finance), a measure for the statistical distribution of portfolio returns
* Price dispersion, a variation in prices across sellers of the same item
*Wage dispersion, the amount of variat ...
. However, it produces simple and tractable mathematical models which are useful for gaining insight into the underlying behavior of a system before these other phenomena are considered.
The AWGN channel is a good model for many satellite
A satellite or artificial satellite is an object intentionally placed into orbit in outer space. Except for passive satellites, most satellites have an electricity generation system for equipment on board, such as solar panels or radioi ...
and deep space communication links. It is not a good model for most terrestrial links because of multipath, terrain blocking, interference, etc. However, for terrestrial path modeling, AWGN is commonly used to simulate background noise of the channel under study, in addition to multipath, terrain blocking, interference, ground clutter and self interference that modern radio systems encounter in terrestrial operation.
Channel capacity
The AWGN channel is represented by a series of outputs at discrete time event index . is the sum of the input and noise, , where isindependent and identically distributed
In probability theory and statistics, a collection of random variables is independent and identically distributed if each random variable has the same probability distribution as the others and all are mutually independent. This property is usual ...
and drawn from a zero-mean normal distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is
:
f(x) = \frac e^
The parameter \mu ...
with variance
In probability theory and statistics, variance is the expectation of the squared deviation of a random variable from its population mean or sample mean. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbe ...
(the noise). The are further assumed to not be correlated with the .
:
:
The capacity of the channel is infinite unless the noise is nonzero, and the are sufficiently constrained. The most common constraint on the input is the so-called "power" constraint, requiring that for a codeword transmitted through the channel, we have:
:
where represents the maximum channel power.
Therefore, the channel capacity for the power-constrained channel is given by:
:
Where is the distribution of . Expand , writing it in terms of the differential entropy
Differential entropy (also referred to as continuous entropy) is a concept in information theory that began as an attempt by Claude Shannon to extend the idea of (Shannon) entropy, a measure of average surprisal of a random variable, to continuo ...
:
:
But and are independent, therefore:
:
Evaluating the differential entropy
Differential entropy (also referred to as continuous entropy) is a concept in information theory that began as an attempt by Claude Shannon to extend the idea of (Shannon) entropy, a measure of average surprisal of a random variable, to continuo ...
of a Gaussian gives:
:
Because and are independent and their sum gives :
:
From this bound, we infer from a property of the differential entropy that
:
Therefore, the channel capacity is given by the highest achievable bound on the mutual information
In probability theory and information theory, the mutual information (MI) of two random variables is a measure of the mutual dependence between the two variables. More specifically, it quantifies the " amount of information" (in units such ...
:
:
Where is maximized when:
:
Thus the channel capacity for the AWGN channel is given by:
:
Channel capacity and sphere packing
Suppose that we are sending messages through the channel with index ranging from to , the number of distinct possible messages. If we encode the messages to bits, then we define the rate as: : A rate is said to be achievable if there is a sequence of codes so that the maximum probability of error tends to zero as approaches infinity. The capacity is the highest achievable rate. Consider a codeword of length sent through the AWGN channel with noise level . When received, the codeword vector variance is now , and its mean is the codeword sent. The vector is very likely to be contained in a sphere of radius around the codeword sent. If we decode by mapping every message received onto the codeword at the center of this sphere, then an error occurs only when the received vector is outside of this sphere, which is very unlikely. Each codeword vector has an associated sphere of received codeword vectors which are decoded to it and each such sphere must map uniquely onto a codeword. Because these spheres therefore must not intersect, we are faced with the problem ofsphere packing
In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space. However, sphere packing p ...
. How many distinct codewords can we pack into our -bit codeword vector? The received vectors have a maximum energy of and therefore must occupy a sphere of radius . Each codeword sphere has radius . The volume of an ''n''-dimensional sphere is directly proportional to , so the maximum number of uniquely decodeable spheres that can be packed into our sphere with transmission power P is:
:
By this argument, the rate R can be no more than .
Achievability
In this section, we show achievability of the upper bound on the rate from the last section. A codebook, known to both encoder and decoder, is generated by selecting codewords of length n, i.i.d. Gaussian with variance and mean zero. For large n, the empirical variance of the codebook will be very close to the variance of its distribution, thereby avoiding violation of the power constraint probabilistically. Received messages are decoded to a message in the codebook which is uniquely jointly typical. If there is no such message or if the power constraint is violated, a decoding error is declared. Let denote the codeword for message , while is, as before the received vector. Define the following three events: # Event :the power of the received message is larger than . # Event : the transmitted and received codewords are not jointly typical. # Event : is in , thetypical set In information theory, the typical set is a set of sequences whose probability is close to two raised to the negative power of the entropy of their source distribution. That this set has total probability close to one is a consequence of the asympt ...
where , which is to say that the incorrect codeword is jointly typical with the received vector.
An error therefore occurs if , or any of the occur. By the law of large numbers, goes to zero as n approaches infinity, and by the joint Asymptotic Equipartition Property
In information theory, the asymptotic equipartition property (AEP) is a general property of the output samples of a stochastic source. It is fundamental to the concept of typical set used in theories of data compression.
Roughly speaking, the th ...
the same applies to . Therefore, for a sufficiently large , both and are each less than . Since and are independent for , we have that and are also independent. Therefore, by the joint AEP, . This allows us to calculate , the probability of error as follows:
:
Therefore, as ''n'' approaches infinity, goes to zero and . Therefore, there is a code of rate R arbitrarily close to the capacity derived earlier.
Coding theorem converse
Here we show that rates above the capacity are not achievable. Suppose that the power constraint is satisfied for a codebook, and further suppose that the messages follow a uniform distribution. Let be the input messages and the output messages. Thus the information flows as: Making use of Fano's inequality gives: where as Let be the encoded message of codeword index i. Then: : Let be the average power of the codeword of index i: : Where the sum is over all input messages . and are independent, thus the expectation of the power of is, for noise level : : And, if is normally distributed, we have that : Therefore, : We may apply Jensen's equality to , a concave (downward) function of ''x'', to get: : Because each codeword individually satisfies the power constraint, the average also satisfies the power constraint. Therefore, : Which we may apply to simplify the inequality above and get: : Therefore, it must be that . Therefore, R must be less than a value arbitrarily close to the capacity derived earlier, as .Effects in time domain
 In serial data communications, the AWGN mathematical model is used to model the timing error caused by random jitter (RJ).
The graph to the right shows an example of timing errors associated with AWGN. The variable Δ''t'' represents the uncertainty in the zero crossing. As the amplitude of the AWGN is increased, the signal-to-noise ratio decreases. This results in increased uncertainty Δ''t''.
When affected by AWGN, the average number of either positive-going or negative-going zero crossings per second at the output of a narrow bandpass filter when the input is a sine wave is
:
:
where
: ''f''0 = the center frequency of the filter,
: ''B'' = the filter bandwidth,
: SNR = the signal-to-noise power ratio in linear terms.
In serial data communications, the AWGN mathematical model is used to model the timing error caused by random jitter (RJ).
The graph to the right shows an example of timing errors associated with AWGN. The variable Δ''t'' represents the uncertainty in the zero crossing. As the amplitude of the AWGN is increased, the signal-to-noise ratio decreases. This results in increased uncertainty Δ''t''.
When affected by AWGN, the average number of either positive-going or negative-going zero crossings per second at the output of a narrow bandpass filter when the input is a sine wave is
:
:
where
: ''f''0 = the center frequency of the filter,
: ''B'' = the filter bandwidth,
: SNR = the signal-to-noise power ratio in linear terms.
Effects in phasor domain
 In modern communication systems, bandlimited AWGN cannot be ignored. When modeling bandlimited AWGN in the phasor domain, statistical analysis reveals that the amplitudes of the real and imaginary contributions are independent variables which follow the
In modern communication systems, bandlimited AWGN cannot be ignored. When modeling bandlimited AWGN in the phasor domain, statistical analysis reveals that the amplitudes of the real and imaginary contributions are independent variables which follow the Gaussian distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is
:
f(x) = \frac e^
The parameter \mu ...
model. When combined, the resultant phasor's magnitude is a Rayleigh-distributed random variable, while the phase is uniformly distributed from 0 to 2π.
The graph to the right shows an example of how bandlimited AWGN can affect a coherent carrier signal. The instantaneous response of the noise vector cannot be precisely predicted, however, its time-averaged response can be statistically predicted. As shown in the graph, we confidently predict that the noise phasor will reside about 38% of the time inside the 1σ circle, about 86% of the time inside the 2σ circle, and about 98% of the time inside the 3σ circle.
See also
*Ground bounce
In electronic engineering, ground bounce is a phenomenon associated with transistor switching where the gate voltage can appear to be less than the local ground potential, causing the unstable operation of a logic gate.
Description
Ground bounc ...
* Noisy-channel coding theorem
In information theory, the noisy-channel coding theorem (sometimes Shannon's theorem or Shannon's limit), establishes that for any given degree of noise contamination of a communication channel, it is possible to communicate discrete data (di ...
* Gaussian process
References
{{Noise Noise (electronics) Time series models