Gyrator–capacitor Model

The gyrator–capacitor model - sometimes also the capacitor-permeance model - is a lumped-element model for magnetic circuits, that can be used in place of the more common resistance–reluctance model. The model makes permeance elements analogous to electrical capacitance (''see magnetic capacitance section'') rather than electrical resistance (''see magnetic reluctance''). Windings are represented as gyrators, interfacing between the electrical circuit and the magnetic model.

The primary advantage of the gyrator–capacitor model compared to the magnetic reluctance model is that the model preserves the correct values of energy flow, storage and dissipation. The gyrator–capacitor model is an example of a group of analogies that preserve energy flow across energy domains by making power conjugate pairs of variables in the various domains analogous. It fills the same role as the impedance analogy for the mechanical domain.

Nomenclature

''Magnetic circuit'' may refer to either the physical magnetic circuit or the model magnetic circuit. Elements and dynamical variables that are part of the model magnetic circuit have names that start with the adjective ''magnetic'', although this convention is not strictly followed. Elements or dynamical variables in the model magnetic circuit may not have a one to one correspondence with components in the physical magnetic circuit. Symbols for elements and variables that are part of the model magnetic circuit may be written with a subscript of M. For example, $C_M$ would be a magnetic capacitor in the model circuit.

Electrical elements in an associated electrical circuit may be brought into the magnetic model for ease of analysis. Model elements in the magnetic circuit that represent electrical elements are typically the electrical dual of the electrical elements. This is because transducers between the electrical and magnetic domains in this model are usually represented by gyrators. A gyrator will transform an element into its dual. For example, a magnetic inductance may represent an electrical capacitance.

Summary of analogy between magnetic circuits and electrical circuits

The following table summarizes the mathematical analogy between electrical circuit theory and magnetic circuit theory.

Gyrator

A gyrator is a two-port element used in network analysis. The gyrator is the complement of the transformer; whereas in a transformer, a voltage on one port will transform to a proportional voltage on the other port, in a gyrator, a voltage on one port will transform to a current on the other port, and vice versa.

The role gyrators play in the gyrator–capacitor model is as transducers between the electrical energy domain and the magnetic energy domain. An emf in the electrical domain is analogous to an mmf in the magnetic domain, and a transducer doing such a conversion would be represented as a transformer. However, real electro-magnetic transducers usually behave as gyrators. A transducer from the magnetic domain to the electrical domain will obey Faraday's law of induction, that is, a rate of change of magnetic flux (a magnetic current in this analogy) produces a proportional emf in the electrical domain. Similarly, a transducer from the electrical domain to the magnetic domain will obey Ampère's circuital law, that is, an electric current will produce a mmf.

A winding of N turns is modeled by a gyrator with a gyration resistance of N ohms.

Transducers that are not based on magnetic induction may not be represented by a gyrator. For instance, a Hall effect sensor is modelled by a transformer.

Magnetic voltage

Magnetic voltage, $v_m$, is an alternate name for ''magnetomotive force'' (mmf), $\mathcal$ (SI unit: A or amp-turn), which is analogous to electrical voltage in an electric circuit. Not all authors use the term ''magnetic voltage''. The magnetomotive force applied to an element between point A and point B is equal to the line integral through the component of the magnetic field strength, $\mathbf$.
$v_m = \mathcal= - \int_A^B \mathbf\cdot d\mathbf$
The resistance–reluctance model uses the same equivalence between magnetic voltage and magnetomotive force.

Magnetic current

Magnetic current, $i_m$, is an alternate name for the ''time rate of change of flux'', $\dot \Phi$ (SI unit: Wb/sec or volts), which is analogous to electrical current in an electric circuit. In the physical circuit, $\dot \Phi$, is magnetic displacement current. The magnetic current flowing through an element of cross section, $S$, is the area integral of the magnetic flux density $\mathbf$.

$i_m = \dot \Phi = \frac \int_S \mathbf \cdot d\mathbf$
The resistance–reluctance model uses a different equivalence, taking magnetic current to be an alternate name for flux, $\Phi$. This difference in the definition of magnetic current is the fundamental difference between the gyrator-capacitor model and the resistance–reluctance model. The definition of magnetic current and magnetic voltage imply the definitions of the other magnetic elements.

Magnetic capacitance

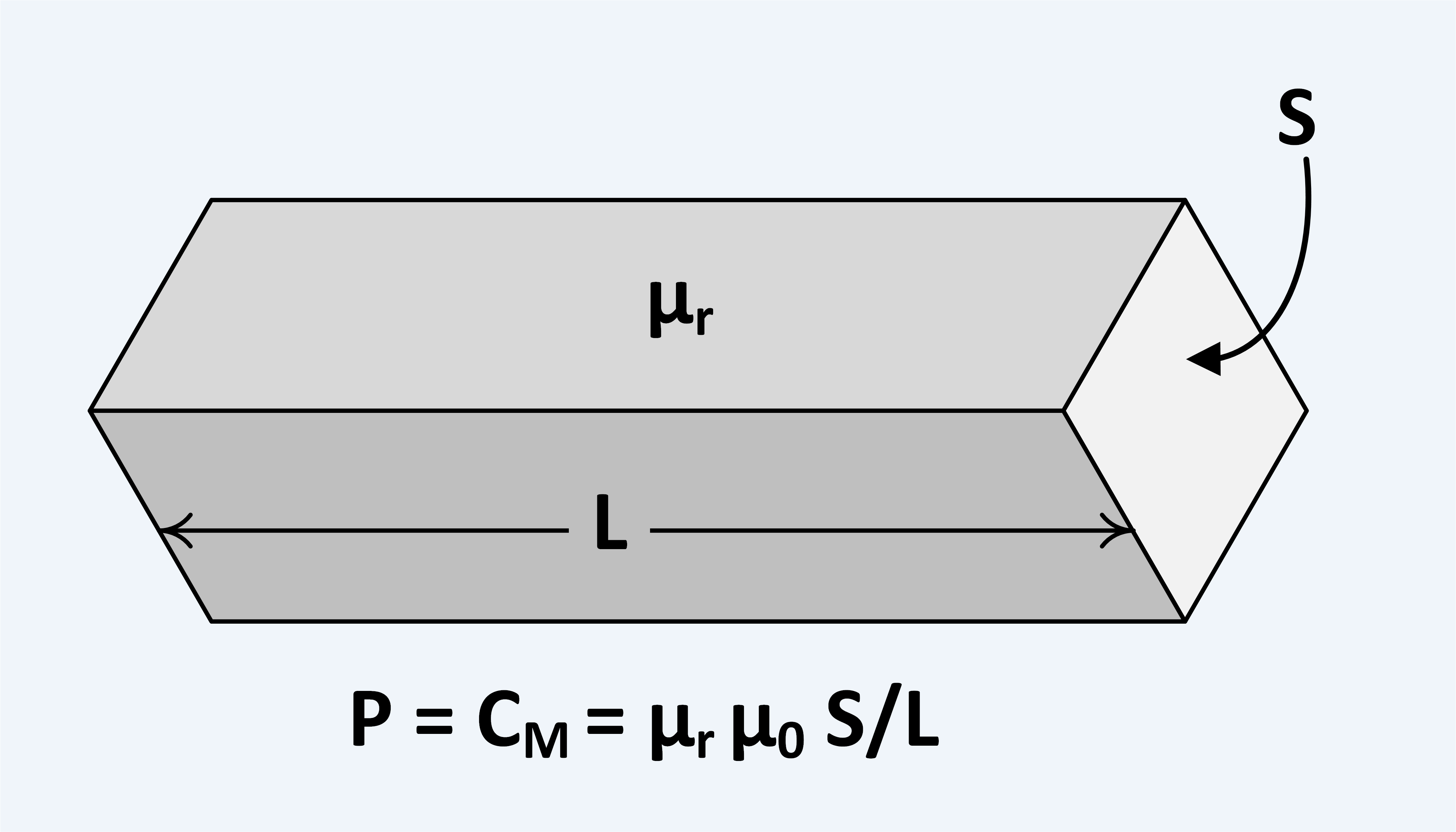
Magnetic capacitance is an alternate name for permeance, (SI unit: H). It is represented by a capacitance in the model magnetic circuit. Some authors use $C_\mathrm$ to denote magnetic capacitance while others use $P$ and refer to the capacitance as a permeance. Permeance of an element is an extensive property defined as the magnetic flux, $\Phi$, through the cross sectional surface of the element divided by the magnetomotive force, $\mathcal$, across the element'
$C_\mathrm = P = \frac= \frac$

For a bar of uniform cross-section, magnetic capacitance is given by,
$C_\mathrm = P=\mu_\mathrm \mu_0\frac$
where:
*$\mu_\mathrm \mu_0 = \mu$ is the magnetic permeability,
*$S$ is the element cross-section, and
*$l$ is the element length.

For phasor analysis, the magnetic permeabilityArkadiew W. ''Eine Theorie des elektromagnetischen Feldes in den ferromagnetischen Metallen''. – Phys. Zs., H. 14, No 19, 1913, S. 928-934. and the permeance are complex values.

Permeance is the reciprocal of reluctance.

Magnetic inductance

In the context of the gyrator-capacitor model of a magnetic circuit, magnetic inductance $L_\mathrm$(SI unit: F) is the analogy to inductance in an electrical circuit.

For phasor analysis the magnetic inductive reactance is:
$x_\mathrm = \omega L_\mathrm$
where:
*$L_\mathrm$ is the magnetic inductance
*$\omega$ is the angular frequency of the magnetic circuit

In the complex form it is a positive imaginary number:
$j x_\mathrm = j\omega L_\mathrm$

The magnetic potential energy sustained by magnetic inductance varies with the frequency of oscillations in electric fields. The average power in a given period is equal to zero. Due to its dependence on frequency, magnetic inductance is mainly observable in magnetic circuits which operate at VHF and/or UHF frequencies.

The notion of magnetic inductance is employed in analysis and computation of circuit behavior in the gyrator–capacitor model in a way analogous to inductance in electrical circuits.

A magnetic inductor can represent an electrical capacitor. A shunt capacitance in the electrical circuit, such as intra-winding capacitance can be represented as a series inductance in the magnetic circuit.

Examples

Three phase transformer

This example shows a three-phase transformer modeled by the gyrator-capacitor approach. The transformer in this example has three primary windings and three secondary windings. The magnetic circuit is split into seven reluctance or permeance elements. Each winding is modeled by a gyrator. The gyration resistance of each gyrator is equal to the number of turns on the associated winding. Each permeance element is modeled by a capacitor. The value of each capacitor in farads is the same as the inductance of the associated permeance in henrys.

N₁, N₂, and N₃ are the number of turns in the three primary windings. N₄, N₅, and N₆ are the number of turns in the three secondary windings. Φ₁, Φ₂, and Φ₃ are the fluxes in the three vertical elements. Magnetic flux in each permeance element in webers is numerically equal to the charge in the associate capacitance in coulombs. The energy in each permeance element is the same as the energy in the associated capacitor.

The schematic shows a three phase generator and a three phase load in addition to the schematic of the transformer model.

Transformer with gap and leakage flux

The gyrator-capacitor approach can accommodate leakage inductance and air gaps in the magnetic circuit. Gaps and leakage flux have a permeance which can be added to the equivalent circuit as capacitors. The permeance of the gap is computed in the same way as the substantive elements, except a relative permeability of unity is used. The permeance of the leakage flux may be difficult to compute due to complex geometry. It may be computed from other considerations such as measurements or specifications.

C_PL and C_SL represent the primary and secondary leakage inductance respectively. C_GAP represents the air gap permeance.

Magnetic impedance

Magnetic complex impedance

Magnetic complex impedance, also called full magnetic resistance, is the quotient of a complex sinusoidal magnetic tension (magnetomotive force, $\mathcal$) on a passive magnetic circuit and the resulting complex sinusoidal magnetic current ($\dot \Phi$) in the circuit. Magnetic impedance is analogous to electrical impedance.

Magnetic complex impedance (SI unit: S) is determined by:
$Z_M = \frac = z_M e^$
where $z_M$ is the modulus of $Z_M$ and $\phi$ is its phase. The argument of a complex magnetic impedance is equal to the difference of the phases of the magnetic tension and magnetic current.
Complex magnetic impedance can be presented in following form:
$Z_M = z_M e^ = z_M \cos \phi + j z_M \sin \phi = r_M + j x_M$
where $r_M = z_M \cos \phi$ is the real part of the complex magnetic impedance, called the effective magnetic resistance, and $x_M = z_M \sin \phi$ is the imaginary part of the complex magnetic impedance, called the reactive magnetic resistance.
The magnetic impedance is equal to
$z_M = \sqrt,$ $\phi = \arctan$

Magnetic effective resistance

Magnetic effective resistance is the real component of complex magnetic impedance. This causes a magnetic circuit to lose magnetic potential energy. Küpfmüller K. Einführung in die theoretische Elektrotechnik, Springer-Verlag, 1959. Active power in a magnetic circuit equals the product of magnetic effective resistance $r_\mathrm$ and magnetic current squared $I_\mathrm^2$.

$P = r_\mathrm I_\mathrm^2$

The magnetic effective resistance on a complex plane appears as the side of the resistance triangle for magnetic circuit of an alternating current. The effective magnetic resistance is bounding with the effective magnetic conductance $g_\mathrm$ by the expression
$g_\mathrm = \frac$
where $z_\mathrm$ is the full magnetic impedance of a magnetic circuit.

Magnetic reactance

Magnetic reactance is the parameter of a passive magnetic circuit, or an element of the circuit, which is equal to the square root of the difference of squares of the magnetic complex impedance and magnetic effective resistance to a magnetic current, taken with the sign plus, if the magnetic current lags behind the magnetic tension in phase, and with the sign minus, if the magnetic current leads the magnetic tension in phase.

Magnetic reactance is the component of magnetic complex impedance of the alternating current circuit, which produces the phase shift between a magnetic current and magnetic tension in the circuit. It is measured in units of $\tfrac$ and is denoted by $x$ (or $X$). It may be inductive $x_L = \omega L_M$ or capacitive $x_C = \tfrac$, where $\omega$ is the angular frequency of a magnetic current, $L_M$ is the magnetic inductiance of a circuit, $C_M$ is the magnetic capacitance of a circuit. The magnetic reactance of an undeveloped circuit with the inductance and the capacitance which are connected in series, is equal: $x = x_L - x_C = \omega L_M - \frac$. If $x_L = x_C$, then the net reactance $x = 0$ and resonance takes place in the circuit. In the general case $x = \sqrt$. When an energy loss is absent ($r = 0$), $x = z$. The angle of the phase shift in a magnetic circuit $\phi = \arctan$. On a complex plane, the magnetic reactance appears as the side of the resistance triangle for circuit of an alternating current.

Limitations of the analogy

The limitations of this analogy between magnetic circuits and electric circuits include the following;

* The current in typical electric circuits is confined to the circuit, with very little "leakage". In typical magnetic circuits not all of the magnetic field is confined to the magnetic circuit because magnetic permeability also exists outside materials (see vacuum permeability). Thus, there may be significant "leakage flux" in the space outside the magnetic cores. If the leakage flux is small compared to the main circuit, it can often be represented as additional elements. In extreme cases, a lumped-element model may not be appropriate at all, and field theory is used instead.
* Magnetic circuits are nonlinear; the permeance in a magnetic circuit is not constant, unlike capacitance in an electrical circuit, but varies depending on the magnetic field. At high magnetic fluxes the ferromagnetic materials used for the cores of magnetic circuits saturate, limiting further increase of the magnetic flux, so above this level the permeance decreases rapidly. In addition, the flux in ferromagnetic materials is subject to hysteresis; it depends not just on the instantaneous MMF but also on the history of MMF. After the source of the magnetic flux is turned off, remanent magnetism is left in ferromagnetic materials, creating flux with no MMF.

References

{{DEFAULTSORT:Gyrator-capacitor model
Electronic engineering
Electrical analogies
Magnetic circuits