Geometry Of Binary Search Trees on:
[Wikipedia]
[Google]
[Amazon]
In computer science, one approach to the
 The key set is .
Let 3, 1, 4, 2 be the access sequence.
* In the first access, only the node 3 is touched.
* In the second access, the nodes 3 and 1 are touched.
* In the third access - 3 and 4 are touched.
* In the fourth access, touch 3, then 1, and after that 2.
The touches are represented geometrically: If an item ''x'' is touched in the operations for the ''i''th access, then a point (''x'',''i'') is plotted.
The key set is .
Let 3, 1, 4, 2 be the access sequence.
* In the first access, only the node 3 is touched.
* In the second access, the nodes 3 and 1 are touched.
* In the third access - 3 and 4 are touched.
* In the fourth access, touch 3, then 1, and after that 2.
The touches are represented geometrically: If an item ''x'' is touched in the operations for the ''i''th access, then a point (''x'',''i'') is plotted.

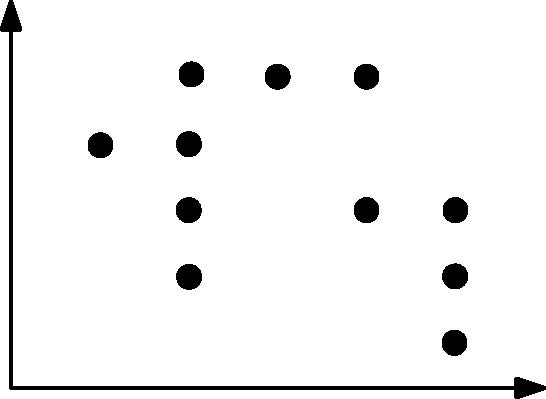 A point set is said to be arborally satisfied if the following property holds: for any
pair of points that do not lie on the same horizontal or vertical line, there exists a third point
which lies in the rectangle spanned by the first two points (either inside or on the boundary).
A point set is said to be arborally satisfied if the following property holds: for any
pair of points that do not lie on the same horizontal or vertical line, there exists a third point
which lies in the rectangle spanned by the first two points (either inside or on the boundary).
dynamic optimality
In computer science, an optimal binary search tree (Optimal BST), sometimes called a weight-balanced binary tree, is a binary search tree which provides the smallest possible search time (or expected search time) for a given sequence of accesses ...
problem on online algorithms for binary search trees involves reformulating the problem geometrically, in terms of augmenting a set of points in the plane with as few additional points as possible in order to avoid rectangles with only two points on their boundary.
Access sequences and competitive ratio
As typically formulated, the online binary search tree problem involves search trees defined over a fixed key set . An ''access sequence'' is a sequence ... where each access belongs to the key set. Any particular algorithm for maintaining binary search trees (such as the splay tree algorithm orIacono's working set structure
In computer science, Iacono's working set structure is a comparison based dictionary. It supports insertion, deletion and access operation to maintain a dynamic set of n elements.
The working set of an item x is the set of elements that have bee ...
) has a ''cost'' for each access sequence that models the amount of time it would take to use the structure to search for each of the keys in the access sequence in turn. The cost of a search is modeled by assuming that the search tree algorithm has a single pointer into a binary search tree, which at the start of each search points to the root of the tree. The algorithm may then perform any sequence of the following operations:
* Move the pointer to its left child.
* Move the pointer to its right child.
* Move the pointer to its parent.
* Perform a single tree rotation on the pointer and its parent.
The search is required, at some point within this sequence of operations to move the pointer to a node containing the key, and the cost of the search is the number of operations that are performed in the sequence. The total cost cost''A''(''X'') for algorithm ''A'' on access sequence ''X'' is the sum of the costs of the searches for each successive key in the sequence.
As is standard in competitive analysis, the competitive ratio Competitive analysis is a method invented for analyzing online algorithms, in which the performance of an online algorithm (which must satisfy an unpredictable sequence of requests, completing each request without being able to see the future) is co ...
of an algorithm ''A'' is defined to be the maximum, over all access sequences, of the ratio of the cost for ''A'' to the best cost that any algorithm could achieve:
:
The dynamic optimality conjecture states that splay trees have constant competitive ratio, but this remains unproven. The geometric view of binary search trees provides a different way of understanding the problem that has led to the development of alternative algorithms that could also (conjecturally) have a constant competitive ratio.
Translation to a geometric point set
In the geometric view of the online binary search tree problem, an ''access sequence'' (sequence of searches performed on a binary search tree (BST) with a key set ) is mapped to the set of points , where the X-axis represents the key space and the Y-axis represents time; to which a set of touched nodes is added. By touched nodes we mean the following. Consider a BST access algorithm with a single pointer to a node in the tree. At the beginning of an access to a given key , this pointer is initialized to the root of the tree. Whenever the pointer moves to or is initialized to a node, we say that the node is touched. We represent a BST algorithm for a given input sequence by drawing a point for each item that gets touched. For example, assume the following BST on 4 nodes is given: The key set is .
Let 3, 1, 4, 2 be the access sequence.
* In the first access, only the node 3 is touched.
* In the second access, the nodes 3 and 1 are touched.
* In the third access - 3 and 4 are touched.
* In the fourth access, touch 3, then 1, and after that 2.
The touches are represented geometrically: If an item ''x'' is touched in the operations for the ''i''th access, then a point (''x'',''i'') is plotted.
The key set is .
Let 3, 1, 4, 2 be the access sequence.
* In the first access, only the node 3 is touched.
* In the second access, the nodes 3 and 1 are touched.
* In the third access - 3 and 4 are touched.
* In the fourth access, touch 3, then 1, and after that 2.
The touches are represented geometrically: If an item ''x'' is touched in the operations for the ''i''th access, then a point (''x'',''i'') is plotted.
Arborally satisfied point sets

 A point set is said to be arborally satisfied if the following property holds: for any
pair of points that do not lie on the same horizontal or vertical line, there exists a third point
which lies in the rectangle spanned by the first two points (either inside or on the boundary).
A point set is said to be arborally satisfied if the following property holds: for any
pair of points that do not lie on the same horizontal or vertical line, there exists a third point
which lies in the rectangle spanned by the first two points (either inside or on the boundary).
Theorem
A point set containing the points is arborally satisfied if and only if it corresponds to a valid BST for the input sequence .Proof
First, prove that the point set for any valid BST algorithm is arborally satisfied. Consider points and , where is touched at time and is touched at time . Assume by symmetry that and . It needs to be shown that there exists a third point in the rectangle with corners as and . Also let denote the lowest common ancestor of nodes and right before time . There are a few cases: * If , then use the point , since must have been touched if was. * If , then the point can be used. * If neither of the above two cases hold, then must be an ancestor of right before time and be an ancestor of right before time . Then at some time , must have been rotated above , so the point can be used. Next, show the other direction: given an arborally satisfied point set, a valid BST corresponding to that point set can be constructed. Organize our BST into a treap which is organized in heap-order by next-touch-time. Note that next-touch-time has ties and is thus not uniquely defined, but this isn’t a problem as long as there is a way to break ties. When time reached, the nodes touched form a connected subtree at the top, by the heap ordering property. Now, assign new next-touch-times for this subtree, and rearrange it into a new local treap. If a pair of nodes, and , straddle the boundary between the touched and untouched part of the treap, then if is to be touched sooner than then is an unsatisfied rectangle because the leftmost such point would be the right child of , not .Corollary
Finding the best BST execution for the input sequence is equivalent to finding the minimum cardinality superset of points (that contains the input in geometric representation) that is arborally satisfied. The more general problem of finding the minimum cardinality arborally satisfied superset of a general set of input points (not limited to one input point per coordinate), is known to be NP-complete.Greedy algorithm
The following greedy algorithm constructs arborally satisfiable sets: * Sweep the point set with a horizontal line by increasing coordinate. * At time , place the minimal number of points at to make the point set up to arborally satisfied. This minimal set of points is uniquely defined: for any unsatisfied rectangle formed with in one corner, add the other corner at . The algorithm has been conjectured to be optimal within an additive term.Other results
The geometry of binary search trees has been used to provide an algorithm which is dynamically optimal if any binary search tree algorithm is dynamically optimal.See also
* Binary search algorithm * Tango trees * Splay trees * Self-balancing binary search tree * Optimal binary search tree * Interleave lower boundReferences
{{Reflist Binary trees Geometry