Geodynamo Between Reversals on:
[Wikipedia]
[Google]
[Amazon]
 In
In
The viscosity of liquid iron at the physical conditions of the Earth's core.
Nature, 392(6678), 805. = 2/day = 7.3×10−5/second and is approximately 107Ω−1m−1 . This gives 2.7×10−4 Tesla. The magnetic field of a magnetic dipole has an inverse cubic dependence in distance, so its order of magnitude at the earth surface can be approximated by multiplying the above result with giving 2.5×10−5 Tesla, not far from to the measured value of 3×10−5 Tesla at the
 Broadly, models of the geodynamo attempt to produce magnetic fields consistent with observed data given certain conditions and equations as mentioned in the sections above. Implementing the magnetohydrodynamic equations successfully was of particular significance because they pushed dynamo models to self-consistency. Though geodynamo models are especially prevalent, dynamo models are not necessarily restricted to the geodynamo; solar and general dynamo models are also of interest. Studying dynamo models has utility in the field of geophysics as doing so can identify how various mechanisms form magnetic fields like those produced by astrophysical bodies like Earth and how they cause magnetic fields to exhibit certain features, such as pole reversals.
The equations used in numerical models of dynamo are highly complex. For decades, theorists were confined to two dimensional ''kinematic dynamo'' models described above, in which the fluid motion is chosen in advance and the effect on the magnetic field calculated. The progression from linear to nonlinear, three dimensional models of dynamo was largely hindered by the search for solutions to magnetohydrodynamic equations, which eliminate the need for many of the assumptions made in kinematic models and allow self-consistency.
Broadly, models of the geodynamo attempt to produce magnetic fields consistent with observed data given certain conditions and equations as mentioned in the sections above. Implementing the magnetohydrodynamic equations successfully was of particular significance because they pushed dynamo models to self-consistency. Though geodynamo models are especially prevalent, dynamo models are not necessarily restricted to the geodynamo; solar and general dynamo models are also of interest. Studying dynamo models has utility in the field of geophysics as doing so can identify how various mechanisms form magnetic fields like those produced by astrophysical bodies like Earth and how they cause magnetic fields to exhibit certain features, such as pole reversals.
The equations used in numerical models of dynamo are highly complex. For decades, theorists were confined to two dimensional ''kinematic dynamo'' models described above, in which the fluid motion is chosen in advance and the effect on the magnetic field calculated. The progression from linear to nonlinear, three dimensional models of dynamo was largely hindered by the search for solutions to magnetohydrodynamic equations, which eliminate the need for many of the assumptions made in kinematic models and allow self-consistency.
 The first ''self-consistent'' dynamo models, ones that determine both the fluid motions and the magnetic field, were developed by two groups in 1995, one in Japan and one in the United States. The latter was made as a model with regards to the geodynamo and received significant attention because it successfully reproduced some of the characteristics of the Earth's field. Following this breakthrough, there was a large swell in development of reasonable, three dimensional dynamo models.
Though many self-consistent models now exist, there are significant differences among the models, both in the results they produce and the way they were developed. Given the complexity of developing a geodynamo model, there are many places where discrepancies can occur such as when making assumptions involving the mechanisms that provide energy for the dynamo, when choosing values for parameters used in equations, or when normalizing equations. In spite of the many differences that may occur, most models have shared features like clear axial dipoles. In many of these models, phenomena like secular variation and geomagnetic polarity reversals have also been successfully recreated.
The first ''self-consistent'' dynamo models, ones that determine both the fluid motions and the magnetic field, were developed by two groups in 1995, one in Japan and one in the United States. The latter was made as a model with regards to the geodynamo and received significant attention because it successfully reproduced some of the characteristics of the Earth's field. Following this breakthrough, there was a large swell in development of reasonable, three dimensional dynamo models.
Though many self-consistent models now exist, there are significant differences among the models, both in the results they produce and the way they were developed. Given the complexity of developing a geodynamo model, there are many places where discrepancies can occur such as when making assumptions involving the mechanisms that provide energy for the dynamo, when choosing values for parameters used in equations, or when normalizing equations. In spite of the many differences that may occur, most models have shared features like clear axial dipoles. In many of these models, phenomena like secular variation and geomagnetic polarity reversals have also been successfully recreated.
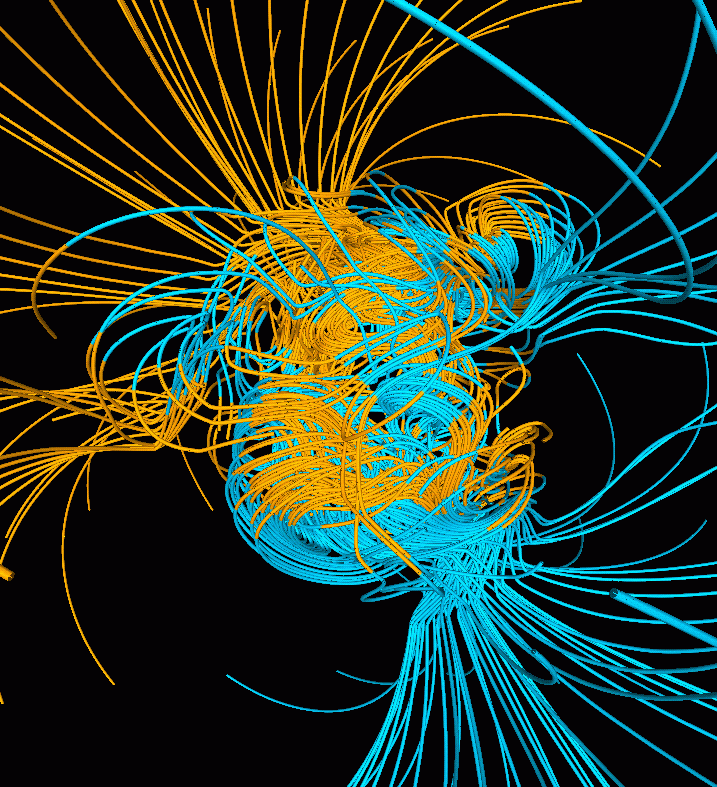 Many observations can be made from dynamo models. Models can be used to estimate how magnetic fields vary with time and can be compared to observed
Many observations can be made from dynamo models. Models can be used to estimate how magnetic fields vary with time and can be compared to observed
physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which rel ...
, the dynamo theory proposes a mechanism by which a celestial body such as Earth
Earth is the third planet from the Sun and the only astronomical object known to harbor life. While large volumes of water can be found throughout the Solar System, only Earth sustains liquid surface water. About 71% of Earth's surf ...
or a star
A star is an astronomical object comprising a luminous spheroid of plasma held together by its gravity. The nearest star to Earth is the Sun. Many other stars are visible to the naked eye at night, but their immense distances from Earth make ...
generates a magnetic field
A magnetic field is a vector field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular to its own velocity and t ...
. The dynamo theory describes the process through which a rotating, convecting, and electrically conducting fluid can maintain a magnetic field over astronomical time scales. A dynamo is thought to be the source of the Earth's magnetic field
Earth's magnetic field, also known as the geomagnetic field, is the magnetic field that extends from Earth's interior out into space, where it interacts with the solar wind, a stream of charged particles emanating from the Sun. The magneti ...
and the magnetic fields of Mercury and the Jovian planets.
History of theory
When William Gilbert published '' de Magnete'' in 1600, he concluded that the Earth is magnetic and proposed the first hypothesis for the origin of this magnetism: permanent magnetism such as that found inlodestone
Lodestones are naturally magnetized pieces of the mineral magnetite. They are naturally occurring magnets, which can attract iron. The property of magnetism was first discovered in antiquity through lodestones. Pieces of lodestone, suspen ...
. In 1919, Joseph Larmor
Sir Joseph Larmor (11 July 1857 – 19 May 1942) was an Irish and British physicist and mathematician who made breakthroughs in the understanding of electricity, dynamics, thermodynamics, and the electron theory of matter. His most influent ...
proposed that a dynamo
"Dynamo Electric Machine" (end view, partly section, )
A dynamo is an electrical generator that creates direct current using a commutator. Dynamos were the first electrical generators capable of delivering power for industry, and the foundat ...
might be generating the field. However, even after he advanced his hypothesis, some prominent scientists advanced alternative explanations. Einstein believed that there might be an asymmetry between the charges of the electron
The electron (, or in nuclear reactions) is a subatomic particle with a negative one elementary electric charge. Electrons belong to the first generation of the lepton particle family,
and are generally thought to be elementary partic ...
and proton so that the Earth's magnetic field
Earth's magnetic field, also known as the geomagnetic field, is the magnetic field that extends from Earth's interior out into space, where it interacts with the solar wind, a stream of charged particles emanating from the Sun. The magneti ...
would be produced by the entire Earth. The Nobel Prize
The Nobel Prizes ( ; sv, Nobelpriset ; no, Nobelprisen ) are five separate prizes that, according to Alfred Nobel's will of 1895, are awarded to "those who, during the preceding year, have conferred the greatest benefit to humankind." Alfre ...
winner Patrick Blackett did a series of experiments looking for a fundamental relation between angular momentum
In physics, angular momentum (rarely, moment of momentum or rotational momentum) is the rotational analog of linear momentum. It is an important physical quantity because it is a conserved quantity—the total angular momentum of a closed sy ...
and magnetic moment
In electromagnetism, the magnetic moment is the magnetic strength and orientation of a magnet or other object that produces a magnetic field. Examples of objects that have magnetic moments include loops of electric current (such as electromagnets ...
, but found none.
Walter M. Elsasser
Walter Maurice Elsasser (March 20, 1904 – October 14, 1991) was a German-born American physicist, a developer of the presently accepted dynamo theory as an explanation of the Earth's magnetism. He proposed that this magnetic field resulted from ...
, considered a "father" of the presently accepted dynamo theory as an explanation of the Earth's magnetism, proposed that this magnetic field resulted from electric currents induced in the fluid outer core of the Earth. He revealed the history of the Earth's magnetic field through pioneering the study of the magnetic orientation of minerals in rocks.
In order to maintain the magnetic field against ohmic decay (which would occur for the dipole field in 20,000 years), the outer core must be convecting. The convection
Convection is single or multiphase fluid flow that occurs spontaneously due to the combined effects of material property heterogeneity and body forces on a fluid, most commonly density and gravity (see buoyancy). When the cause of the c ...
is likely some combination of thermal and compositional convection. The mantle controls the rate at which heat is extracted from the core. Heat sources include gravitational energy released by the compression of the core, gravitational energy released by the rejection of light elements (probably sulfur
Sulfur (or sulphur in British English) is a chemical element with the symbol S and atomic number 16. It is abundant, multivalent and nonmetallic. Under normal conditions, sulfur atoms form cyclic octatomic molecules with a chemical formul ...
, oxygen
Oxygen is the chemical element with the symbol O and atomic number 8. It is a member of the chalcogen group in the periodic table, a highly reactive nonmetal, and an oxidizing agent that readily forms oxides with most elements as we ...
, or silicon
Silicon is a chemical element with the symbol Si and atomic number 14. It is a hard, brittle crystalline solid with a blue-grey metallic luster, and is a tetravalent metalloid and semiconductor. It is a member of group 14 in the periodic ...
) at the inner core boundary as it grows, latent heat of crystallization at the inner core boundary, and radioactivity of potassium
Potassium is the chemical element with the symbol K (from Neo-Latin '' kalium'') and atomic number19. Potassium is a silvery-white metal that is soft enough to be cut with a knife with little force. Potassium metal reacts rapidly with atmosp ...
, uranium
Uranium is a chemical element with the symbol U and atomic number 92. It is a silvery-grey metal in the actinide series of the periodic table. A uranium atom has 92 protons and 92 electrons, of which 6 are valence electrons. Uranium is weakly ...
and thorium
Thorium is a weakly radioactive metallic chemical element with the symbol Th and atomic number 90. Thorium is silvery and tarnishes black when it is exposed to air, forming thorium dioxide; it is moderately soft and malleable and has a high ...
.
At the dawn of the 21st century, numerical modeling of the Earth's magnetic field has not been successfully demonstrated. Initial models are focused on field generation by convection in the planet's fluid outer core. It was possible to show the generation of a strong, Earth-like field when the model assumed a uniform core-surface temperature and exceptionally high viscosities for the core fluid. Computations which incorporated more realistic parameter values yielded magnetic fields that were less Earth-like, but indicated that model refinements may ultimately lead to an accurate analytic model. Slight variations in the core-surface temperature, in the range of a few millikelvins, result in significant increases in convective flow and produce more realistic magnetic fields.
Formal definition
Dynamo theory describes the process through which a rotating, convecting, and electrically conducting fluid acts to maintain a magnetic field. This theory is used to explain the presence of anomalously long-lived magnetic fields in astrophysical bodies. The conductive fluid in the geodynamo is liquid iron in the outer core, and in thesolar dynamo
The solar dynamo is a physical process that generates the Sun's magnetic field. It is explained with a variant of the dynamo theory. A naturally occurring electric generator in the Sun's interior produces electric currents and a magnetic field, ...
is ionized gas at the tachocline. Dynamo theory of astrophysical bodies uses magnetohydrodynamic equations to investigate how the fluid can continuously regenerate the magnetic field.
It was once believed that the dipole
In physics, a dipole () is an electromagnetic phenomenon which occurs in two ways:
*An electric dipole deals with the separation of the positive and negative electric charges found in any electromagnetic system. A simple example of this system ...
, which comprises much of the Earth's magnetic field
Earth's magnetic field, also known as the geomagnetic field, is the magnetic field that extends from Earth's interior out into space, where it interacts with the solar wind, a stream of charged particles emanating from the Sun. The magneti ...
and is misaligned along the rotation axis by 11.3 degrees, was caused by permanent magnetization of the materials in the earth. This means that dynamo theory was originally used to explain the Sun's magnetic field in its relationship with that of the Earth. However, this hypothesis, which was initially proposed by Joseph Larmor
Sir Joseph Larmor (11 July 1857 – 19 May 1942) was an Irish and British physicist and mathematician who made breakthroughs in the understanding of electricity, dynamics, thermodynamics, and the electron theory of matter. His most influent ...
in 1919, has been modified due to extensive studies of magnetic secular variation, paleomagnetism
Paleomagnetism (or palaeomagnetismsee ), is the study of magnetic fields recorded in rocks, sediment, or archeological materials. Geophysicists who specialize in paleomagnetism are called ''paleomagnetists.''
Certain magnetic minerals in roc ...
(including polarity reversal
Polarity may refer to:
Science
*Electrical polarity, direction of electrical current
*Polarity (mutual inductance), the relationship between components such as transformer windings
*Polarity (projective geometry), in mathematics, a duality of orde ...
s), seismology, and the solar system's abundance of elements. Also, the application of the theories of Carl Friedrich Gauss
Johann Carl Friedrich Gauss (; german: Gauß ; la, Carolus Fridericus Gauss; 30 April 177723 February 1855) was a German mathematician and physicist who made significant contributions to many fields in mathematics and science. Sometimes refe ...
to magnetic observations showed that Earth's magnetic field had an internal, rather than external, origin.
There are three requisites for a dynamo to operate:
*An electrically conductive fluid medium
*Kinetic energy provided by planetary rotation
*An internal energy source to drive convective motions within the fluid.
In the case of the Earth, the magnetic field is induced and constantly maintained by the convection of liquid iron in the outer core. A requirement for the induction of field is a rotating fluid. Rotation in the outer core is supplied by the Coriolis effect
In physics, the Coriolis force is an inertial or fictitious force that acts on objects in motion within a frame of reference that rotates with respect to an inertial frame. In a reference frame with clockwise rotation, the force acts to the ...
caused by the rotation of the Earth. The Coriolis force tends to organize fluid motions and electric currents into columns (also see Taylor column
A Taylor column is a fluid dynamics phenomenon that occurs as a result of the Coriolis effect. It was named after Geoffrey Ingram Taylor. Rotating fluids that are perturbed by a solid body tend to form columns parallel to the axis of rotation ca ...
s) aligned with the rotation axis. Induction or creation of magnetic field is described by the induction equation:
:
where u is velocity, B is magnetic field, ''t'' is time, and is the magnetic diffusivity with electrical conductivity and permeability. The ratio of the second term on the right hand side to the first term gives the magnetic Reynolds number, a dimensionless ratio of advection of magnetic field to diffusion.
Tidal heating supporting a dynamo
Tidal forces between celestial orbiting bodies cause friction that heats up their interiors. This is known as tidal heating, and it helps keep the interior in a liquid state. A liquid interior that can conduct electricity is required to produce a dynamo. Saturn's Enceladus and Jupiter's Io have enough tidal heating to liquify their inner cores, but they may not create a dynamo because they cannot conduct electricity. Mercury, despite its small size, has a magnetic field, because it has a conductive liquid core created by its iron composition and friction resulting from its highly elliptical orbit. It is theorized that the Moon once had a magnetic field, based on evidence from magnetized lunar rocks, due to its short-lived closer distance to Earth creating tidal heating. An orbit and rotation of a planet helps provide a liquid core, and supplements kinetic energy that supports a dynamo action.Kinematic dynamo theory
In kinematic dynamo theory the velocity field is ''prescribed'', instead of being a dynamic variable: The model makes no provision for the flow distorting in response to the magnetic field. This method cannot provide the time variable behaviour of a fully nonlinear chaotic dynamo, but can be used to study how magnetic field strength varies with the flow structure and speed. UsingMaxwell's equations
Maxwell's equations, or Maxwell–Heaviside equations, are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, and electric circuits.
Th ...
simultaneously with the curl of Ohm's law
Ohm's law states that the current through a conductor between two points is directly proportional to the voltage across the two points. Introducing the constant of proportionality, the resistance, one arrives at the usual mathematical equatio ...
, one can derive what is basically a linear eigenvalue equation for magnetic fields (), which can be done when assuming that the magnetic field is independent from the velocity field. One arrives at a critical '' magnetic Reynolds number'', above which the flow strength is sufficient to amplify the imposed magnetic field, and below which the magnetic field dissipates.
Practical measure of possible dynamos
The most functional feature of kinematic dynamo theory is that it can be used to test whether a velocity field is or is not capable of dynamo action. By experimentally applying a certain velocity field to a small magnetic field, one can observe whether the magnetic field tends to grow (or not) in response to the applied flow. If the magnetic field does grow, then the system is either capable of dynamo action or is a dynamo, but if the magnetic field does not grow, then it is simply referred to as “not a dynamo”. An analogous method called the '' membrane paradigm'' is a way of looking atblack hole
A black hole is a region of spacetime where gravity is so strong that nothing, including light or other electromagnetic waves, has enough energy to escape it. The theory of general relativity predicts that a sufficiently compact mass can defo ...
s that allows for the material near their surfaces to be expressed in the language of dynamo theory.
Spontaneous breakdown of a topological supersymmetry
Kinematic dynamo can be also viewed as the phenomenon of the spontaneous breakdown of the topological supersymmetry of the associated stochastic differential equation related to the flow of the background matter. Within stochastic supersymmetric theory, this supersymmetry is an intrinsic property of ''all''stochastic differential equation
A stochastic differential equation (SDE) is a differential equation in which one or more of the terms is a stochastic process, resulting in a solution which is also a stochastic process. SDEs are used to model various phenomena such as stock ...
s, its interpretation is that the model’s phase space preserves continuity via continuous time flows. When the continuity of that flow spontaneously breaks down, the system is in the stochastic state of ''deterministic chaos''. In other words, kinematic dynamo arises because of chaotic flow in the underlying background matter.
Nonlinear dynamo theory
The kinematic approximation becomes invalid when the magnetic field becomes strong enough to affect the fluid motions. In that case the velocity field becomes affected by theLorentz force
In physics (specifically in electromagnetism) the Lorentz force (or electromagnetic force) is the combination of electric and magnetic force on a point charge due to electromagnetic fields. A particle of charge moving with a velocity in an ele ...
, and so the induction equation is no longer linear in the magnetic field. In most cases this leads to a quenching of the amplitude of the dynamo. Such dynamos are sometimes also referred to as ''hydromagnetic dynamos''.
Virtually all dynamos in astrophysics and geophysics are hydromagnetic dynamos.
The main idea of the theory is that any small magnetic field existing in the outer core creates currents in the moving fluid there due to Lorentz force. These currents create further magnetic field due to Ampere's law. With the fluid motion, the currents are carried in a way that the magnetic field gets stronger (as long as is negative). Thus a "seed" magnetic field can get stronger and stronger until it reaches some value that is related to existing non-magnetic forces.
Numerical models are used to simulate fully nonlinear dynamos. The following equations are used:
*The induction equation, presented above.
*Maxwell's equations for negligible electric field:
::
::
*The continuity equation
A continuity equation or transport equation is an equation that describes the transport of some quantity. It is particularly simple and powerful when applied to a conserved quantity, but it can be generalized to apply to any extensive quantity. ...
for conservation of mass
In physics and chemistry, the law of conservation of mass or principle of mass conservation states that for any system closed to all transfers of matter and energy, the mass of the system must remain constant over time, as the system's mass ca ...
, for which the Boussinesq approximation is often used:
::
*The Navier-Stokes equation for conservation of momentum
In Newtonian mechanics, momentum (more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. If is an object's mass ...
, again in the same approximation, with the magnetic force and gravitation force as the external forces:
::
:where is the kinematic viscosity
The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water.
Viscosity quantifies the inte ...
, is the mean density and is the relative density perturbation that provides buoyancy (for thermal convection where is coefficient of thermal expansion
Thermal expansion is the tendency of matter to change its shape, area, volume, and density in response to a change in temperature, usually not including phase transitions.
Temperature is a monotonic function of the average molecular kinetic ...
), is the rotation rate of the Earth, and is the electric current density.
*A transport equation, usually of heat (sometimes of light element concentration):
::
:where is temperature, is the thermal diffusivity with thermal conductivity, heat capacity, and density, and is an optional heat source. Often the pressure is the dynamic pressure, with the hydrostatic pressure and centripetal potential removed.
These equations are then non-dimensionalized, introducing the non-dimensional parameters,
:
where is the Rayleigh number, the Ekman number
The Ekman number (Ek) is a dimensionless number used in fluid dynamics to describe the ratio of viscous forces to Coriolis forces. It is frequently used in describing geophysical phenomena in the oceans and atmosphere in order to characterise the r ...
, and the Prandtl and magnetic Prandtl number The Magnetic Prandtl number (Prm) is a dimensionless quantity occurring in magnetohydrodynamics which approximates the ratio of momentum diffusivity (viscosity) and magnetic diffusivity. It is defined as:
:\mathrm_\mathrm = \frac = \frac = \frac
...
. Magnetic field scaling is often in Elsasser number units
Energy conversion between magnetic and kinematic energy
The scalar product of the above form of Navier-Stokes equation with gives the rate of increase of kinetic energy density, , on the left-hand side. The last term on the right-hand side is then , the local contribution to the kinetic energy due toLorentz force
In physics (specifically in electromagnetism) the Lorentz force (or electromagnetic force) is the combination of electric and magnetic force on a point charge due to electromagnetic fields. A particle of charge moving with a velocity in an ele ...
.
The scalar product of the induction equation with gives the rate of increase of the magnetic energy density, , on the left-hand side. The last term on the right-hand side is then Since the equation is volume-integrated, this term is equivalent up to a boundary term (and with the double use of the scalar triple product identity) to (where one of Maxwell's equations was used). This is the local contribution to the magnetic energy due to fluid motion.
Thus the term is the rate of transformation of kinetic energy to magnetic energy. This has to be non-negative at least in part of the volume, for the dynamo to produce magnetic field.
From the diagram above, it is not clear why this term should be positive. A simple argument can be based on consideration of net effects. To create the magnetic field, the net electric current must wrap around the axis of rotation of the planet. In that case, for the term to be positive, the net flow of conducting matter must be towards the axis of rotation. The diagram only shows a net flow from the poles to the equator. However mass conservation requires an additional flow from the equator toward the poles. If that flow was along the axis of rotation, that implies the circulation would be completed by a flow from the ones shown towards the axis of rotation, producing the desired effect.
Order of magnitude of the magnetic field created by Earth's dynamo
The above formula for the rate of conversion of kinetic energy to magnetic energy, is equivalent to a rate of work done by a force of on the outer core matter, whose velocity is . This work is the result of non-magnetic forces acting on the fluid. Of those, the gravitational force and thecentrifugal force
In Newtonian mechanics, the centrifugal force is an inertial force (also called a "fictitious" or "pseudo" force) that appears to act on all objects when viewed in a rotating frame of reference. It is directed away from an axis which is parallel ...
are conservative
Conservatism is a cultural, social, and political philosophy that seeks to promote and to preserve traditional institutions, practices, and values. The central tenets of conservatism may vary in relation to the culture and civilization in ...
and therefore have no overall contribution to fluid moving in closed loops. Ekman number (defined above), which is the ratio between the two remaining forces, namely the viscosity and Coriolis force, is very low inside Earth's outer core, because its viscosity is low (1.2–1.5 ×10 pascal-second) due to its liquidity.
Thus the main time-averaged contribution to the work is from Coriolis force, whose size is though this quantity and are related only indirectly and are not in general equal locally (thus they affect each other but not in the same place and time).
The current density is itself the result of the magnetic field according to Ohm's law
Ohm's law states that the current through a conductor between two points is directly proportional to the voltage across the two points. Introducing the constant of proportionality, the resistance, one arrives at the usual mathematical equatio ...
. Again, due to matter motion and current flow, this is not necessarily the field at the same place and time. However these relations can still be used to deduce orders of magnitude of the quantities in question.
In terms of order of magnitude, and , giving or:
:
The exact ratio between both sides is the square root of Elsasser number.
Note that the magnetic field direction cannot be inferred from this approximation (at least not its sign) as it appears squared, and is, indeed, sometimes reversed
Reversal may refer to:
* Medical reversal, when a medical intervention falls out of use after improved clinical trials demonstrate its ineffectiveness or harmfulness.
* Reversal (law), the setting aside of a decision of a lower court by a higher c ...
, though in general it lies on a similar axis to that of .
For earth outer core, is approximately 104 kg/m3,de Wijs, G. A., Kresse, G., Vočadlo, L., Dobson, D., Alfe, D., Gillan, M. J., & Price, G. D. (1998)The viscosity of liquid iron at the physical conditions of the Earth's core.
Nature, 392(6678), 805. = 2/day = 7.3×10−5/second and is approximately 107Ω−1m−1 . This gives 2.7×10−4 Tesla. The magnetic field of a magnetic dipole has an inverse cubic dependence in distance, so its order of magnitude at the earth surface can be approximated by multiplying the above result with giving 2.5×10−5 Tesla, not far from to the measured value of 3×10−5 Tesla at the
equator
The equator is a circle of latitude, about in circumference, that divides Earth into the Northern and Southern hemispheres. It is an imaginary line located at 0 degrees latitude, halfway between the North and South poles. The term can al ...
.
Numerical models
 Broadly, models of the geodynamo attempt to produce magnetic fields consistent with observed data given certain conditions and equations as mentioned in the sections above. Implementing the magnetohydrodynamic equations successfully was of particular significance because they pushed dynamo models to self-consistency. Though geodynamo models are especially prevalent, dynamo models are not necessarily restricted to the geodynamo; solar and general dynamo models are also of interest. Studying dynamo models has utility in the field of geophysics as doing so can identify how various mechanisms form magnetic fields like those produced by astrophysical bodies like Earth and how they cause magnetic fields to exhibit certain features, such as pole reversals.
The equations used in numerical models of dynamo are highly complex. For decades, theorists were confined to two dimensional ''kinematic dynamo'' models described above, in which the fluid motion is chosen in advance and the effect on the magnetic field calculated. The progression from linear to nonlinear, three dimensional models of dynamo was largely hindered by the search for solutions to magnetohydrodynamic equations, which eliminate the need for many of the assumptions made in kinematic models and allow self-consistency.
Broadly, models of the geodynamo attempt to produce magnetic fields consistent with observed data given certain conditions and equations as mentioned in the sections above. Implementing the magnetohydrodynamic equations successfully was of particular significance because they pushed dynamo models to self-consistency. Though geodynamo models are especially prevalent, dynamo models are not necessarily restricted to the geodynamo; solar and general dynamo models are also of interest. Studying dynamo models has utility in the field of geophysics as doing so can identify how various mechanisms form magnetic fields like those produced by astrophysical bodies like Earth and how they cause magnetic fields to exhibit certain features, such as pole reversals.
The equations used in numerical models of dynamo are highly complex. For decades, theorists were confined to two dimensional ''kinematic dynamo'' models described above, in which the fluid motion is chosen in advance and the effect on the magnetic field calculated. The progression from linear to nonlinear, three dimensional models of dynamo was largely hindered by the search for solutions to magnetohydrodynamic equations, which eliminate the need for many of the assumptions made in kinematic models and allow self-consistency.
 The first ''self-consistent'' dynamo models, ones that determine both the fluid motions and the magnetic field, were developed by two groups in 1995, one in Japan and one in the United States. The latter was made as a model with regards to the geodynamo and received significant attention because it successfully reproduced some of the characteristics of the Earth's field. Following this breakthrough, there was a large swell in development of reasonable, three dimensional dynamo models.
Though many self-consistent models now exist, there are significant differences among the models, both in the results they produce and the way they were developed. Given the complexity of developing a geodynamo model, there are many places where discrepancies can occur such as when making assumptions involving the mechanisms that provide energy for the dynamo, when choosing values for parameters used in equations, or when normalizing equations. In spite of the many differences that may occur, most models have shared features like clear axial dipoles. In many of these models, phenomena like secular variation and geomagnetic polarity reversals have also been successfully recreated.
The first ''self-consistent'' dynamo models, ones that determine both the fluid motions and the magnetic field, were developed by two groups in 1995, one in Japan and one in the United States. The latter was made as a model with regards to the geodynamo and received significant attention because it successfully reproduced some of the characteristics of the Earth's field. Following this breakthrough, there was a large swell in development of reasonable, three dimensional dynamo models.
Though many self-consistent models now exist, there are significant differences among the models, both in the results they produce and the way they were developed. Given the complexity of developing a geodynamo model, there are many places where discrepancies can occur such as when making assumptions involving the mechanisms that provide energy for the dynamo, when choosing values for parameters used in equations, or when normalizing equations. In spite of the many differences that may occur, most models have shared features like clear axial dipoles. In many of these models, phenomena like secular variation and geomagnetic polarity reversals have also been successfully recreated.
Observations
 Many observations can be made from dynamo models. Models can be used to estimate how magnetic fields vary with time and can be compared to observed
Many observations can be made from dynamo models. Models can be used to estimate how magnetic fields vary with time and can be compared to observed paleomagnetic
Paleomagnetism (or palaeomagnetismsee ), is the study of magnetic fields recorded in rocks, sediment, or archeological materials. Geophysicists who specialize in paleomagnetism are called ''paleomagnetists.''
Certain magnetic minerals in rocks ...
data to find similarities between the model and the Earth. Due to the uncertainty of paleomagnetic observations, however, comparisons may not be entirely valid or useful. Simplified geodynamo models have shown relationships between the dynamo number (determined by variance in rotational rates in the outer core and mirror-asymmetric convection (e.g. when convection favors one direction in the north and the other in the south)) and magnetic pole reversals as well as found similarities between the geodynamo and the Sun's dynamo. In many models, it appears that magnetic fields have somewhat random magnitudes that follow a normal trend that average to zero. In addition to these observations, general observations about the mechanisms powering the geodynamo can be made based on how accurately the model reflects actual data collected from Earth.
Modern modelling
The complexity of dynamo modelling is so great that models of the geodynamo are limited by the current power of supercomputers, particularly because calculating theEkman Ekman is a Swedish surname. Notable people with the surname include:
* Carl Gustaf Ekman (1872–1945), Swedish politician
*Carl Daniel Ekman (1845–1904), Swedish chemical engineer
* Erik Leonard Ekman (1883–1931), Swedish botanist
* Fam Ekman ...
and Rayleigh Rayleigh may refer to:
Science
*Rayleigh scattering
*Rayleigh–Jeans law
*Rayleigh waves
*Rayleigh (unit), a unit of photon flux named after the 4th Baron Rayleigh
*Rayl, rayl or Rayleigh, two units of specific acoustic impedance and characte ...
number of the outer core is extremely difficult and requires a vast number of computations.
Many improvements have been proposed in dynamo modelling since the self-consistent breakthrough in 1995. One suggestion in studying the complex magnetic field changes is applying spectral methods to simplify computations. Ultimately, until considerable improvements in computer power are made, the methods for computing realistic dynamo models will have to be made more efficient, so making improvements in methods for computing the model is of high importance for the advancement of numerical dynamo modelling.
See also
* Antidynamo theorem * Rotating magnetic field * Secular variationReferences
* * * * * {{DEFAULTSORT:Dynamo Theory Geomagnetism Plasma physics Magnetohydrodynamics Structure of the Earth Computational physics Unsolved problems in physics Magnetism in astronomy