Geodesics Of The Schwarzschild Vacuum on:
[Wikipedia]
[Google]
[Amazon]
In
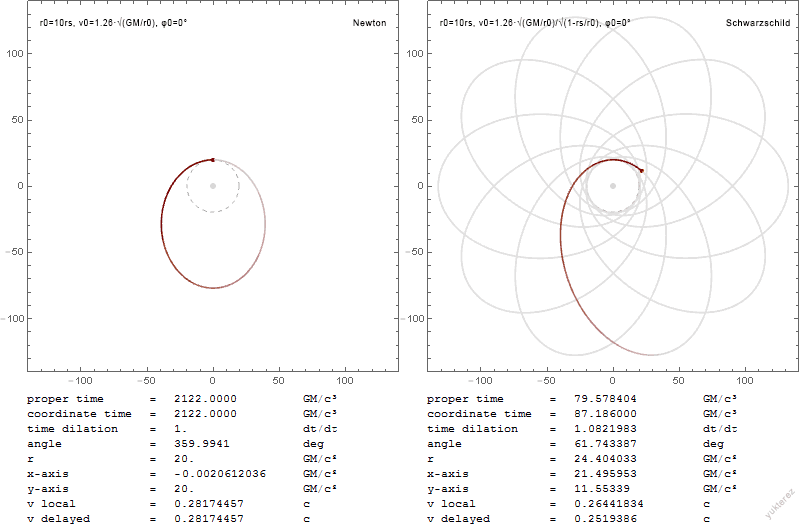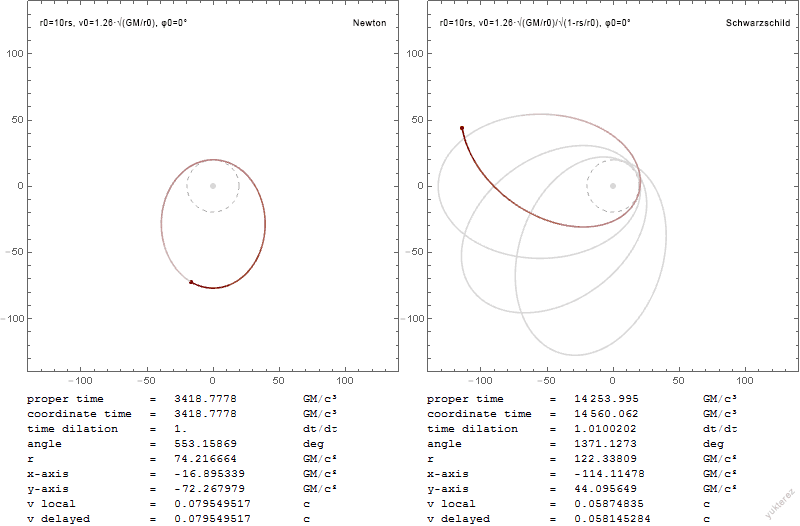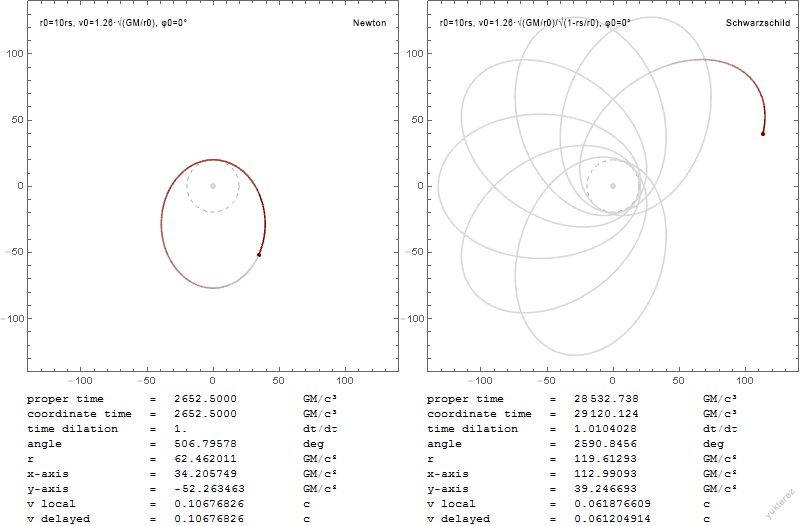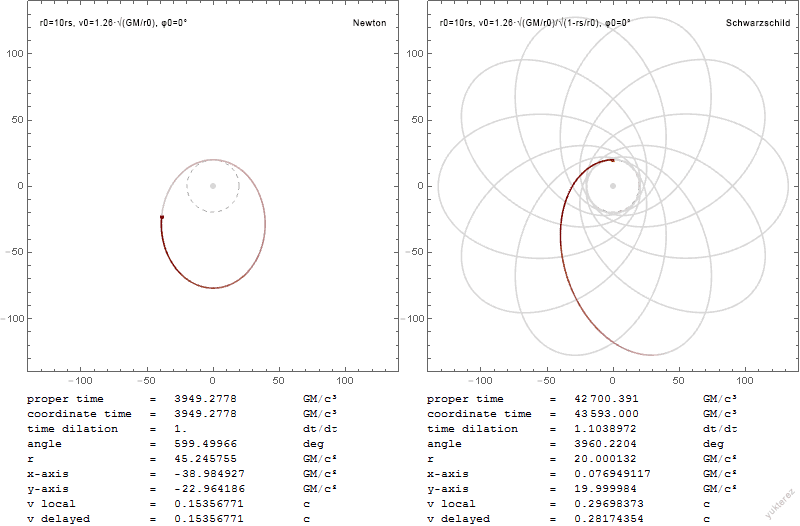 We may simplify the problem by using symmetry to eliminate one variable from consideration. Since the Schwarzschild metric is symmetrical about , any geodesic that begins moving in that plane will remain in that plane indefinitely (the plane is
We may simplify the problem by using symmetry to eliminate one variable from consideration. Since the Schwarzschild metric is symmetrical about , any geodesic that begins moving in that plane will remain in that plane indefinitely (the plane is
 In the limit as the particle mass ''m'' goes to zero (or, equivalently if the light is heading directly toward the central mass, as the length-scale ''a'' goes to infinity), the equation for the orbit becomes
:
Expanding in powers of , the leading order term in this formula gives the approximate angular deflection δ''φ'' for a massless particle coming in from infinity and going back out to infinity:
:
Here, is the
In the limit as the particle mass ''m'' goes to zero (or, equivalently if the light is heading directly toward the central mass, as the length-scale ''a'' goes to infinity), the equation for the orbit becomes
:
Expanding in powers of , the leading order term in this formula gives the approximate angular deflection δ''φ'' for a massless particle coming in from infinity and going back out to infinity:
:
Here, is the
 The effective potential can be re-written in terms of the length .
:
Circular orbits are possible when the effective force is zero
:
i.e., when the two attractive forces — Newtonian gravity (first term) and the attraction unique to general relativity (third term) — are exactly balanced by the repulsive centrifugal force (second term). There are two radii at which this balancing can occur, denoted here as ''r''inner and ''r''outer
:
which are obtained using the
The effective potential can be re-written in terms of the length .
:
Circular orbits are possible when the effective force is zero
:
i.e., when the two attractive forces — Newtonian gravity (first term) and the attraction unique to general relativity (third term) — are exactly balanced by the repulsive centrifugal force (second term). There are two radii at which this balancing can occur, denoted here as ''r''inner and ''r''outer
:
which are obtained using the  Substituting the definitions of and ''r''s into ''r''outer yields the classical formula for a particle of mass orbiting a body of mass .
:
where ''ω''φ is the orbital angular speed of the particle. This formula is obtained in non-relativistic mechanics by setting the
Substituting the definitions of and ''r''s into ''r''outer yields the classical formula for a particle of mass orbiting a body of mass .
:
where ''ω''φ is the orbital angular speed of the particle. This formula is obtained in non-relativistic mechanics by setting the
 The orbital precession rate may be derived using this radial effective potential ''V''. A small radial deviation from a circular orbit of radius ''r''outer will oscillate stably with an angular frequency
:
which equals
:
Taking the square root of both sides and performing a
The orbital precession rate may be derived using this radial effective potential ''V''. A small radial deviation from a circular orbit of radius ''r''outer will oscillate stably with an angular frequency
:
which equals
:
Taking the square root of both sides and performing a
 The orbital equation can be derived from the Hamilton–Jacobi equation.Landau and Lifshitz, pp. 306–307; Misner, Thorne, and Wheeler, pp. 636–679. The advantage of this approach is that it equates the motion of the particle with the propagation of a wave, and leads neatly into the derivation of the deflection of light by gravity in
The orbital equation can be derived from the Hamilton–Jacobi equation.Landau and Lifshitz, pp. 306–307; Misner, Thorne, and Wheeler, pp. 636–679. The advantage of this approach is that it equates the motion of the particle with the propagation of a wave, and leads neatly into the derivation of the deflection of light by gravity in
scan of the original paper
*
text of the original paper, in Wikisource
*
translation by Antoci and Loinger
*
a commentary on the paper, giving a simpler derivation
* Schwarzschild, K. (1916). Über das Gravitationsfeld einer Kugel aus inkompressibler Flüssigkeit. ''Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften'' 1, 424-?. * * * * * * * (See
389
ndash;393 , isbn = 978-1-114-28944-4
from ''Reflections on Relativity'' by Kevin Brown. Exact solutions in general relativity
general relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics ...
, Schwarzschild geodesics describe the motion of test particles in the gravitational field of a central fixed mass that is, motion in the Schwarzschild metric. Schwarzschild geodesics have been pivotal in the validation of Einstein's theory of general relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics ...
. For example, they provide accurate predictions of the anomalous precession of the planets in the Solar System and of the deflection of light by gravity.
Schwarzschild geodesics pertain only to the motion of particles of masses so small they contribute little to the gravitational field. However, they are highly accurate in many astrophysical scenarios provided that is many-fold smaller than the central mass , e.g., for planets orbiting their sun. Schwarzschild geodesics are also a good approximation to the relative motion of two bodies of arbitrary mass, provided that the Schwarzschild mass is set equal to the sum of the two individual masses and . This is important in predicting the motion of binary stars in general relativity.
Historical context
The Schwarzschild metric is named in honour of its discovererKarl Schwarzschild
Karl Schwarzschild (; 9 October 1873 – 11 May 1916) was a German physicist and astronomer.
Schwarzschild provided the first exact solution to the Einstein field equations of general relativity, for the limited case of a single spherical non-r ...
, who found the solution in 1915, only about a month after the publication of Einstein's theory of general relativity. It was the first exact solution of the Einstein field equations other than the trivial flat space solution.
In 1931, Yusuke Hagihara published a paper showing that the trajectory of a test particle in the Schwarzschild metric can be expressed in terms of elliptic functions.
Schwarzschild metric
An exact solution to theEinstein field equations
In the general theory of relativity, the Einstein field equations (EFE; also known as Einstein's equations) relate the geometry of spacetime to the distribution of matter within it.
The equations were published by Einstein in 1915 in the form ...
is the Schwarzschild metric, which corresponds to the external gravitational field of an uncharged, non-rotating, spherically symmetric body of mass . The Schwarzschild solution can be written asLandau and Lifshitz, pp. 299–301.
:
where
: , in the case of a test particle In physical theories, a test particle, or test charge, is an idealized model of an object whose physical properties (usually mass, charge, or size) are assumed to be negligible except for the property being studied, which is considered to be insuf ...
of small positive mass, is the proper time (time measured by a clock moving with the particle) in seconds,
: is the speed of light
The speed of light in vacuum, commonly denoted , is a universal physical constant that is important in many areas of physics. The speed of light is exactly equal to ). According to the special theory of relativity, is the upper limit ...
in meters per second,
: is, for , the time coordinate (time measured by a stationary clock at infinity) in seconds,
: is, for , the radial coordinate (circumference of a circle centered at the star divided by ) in meters,
: is the colatitude (angle from North) in radians,
: is the longitude
Longitude (, ) is a geographic coordinate that specifies the east– west position of a point on the surface of the Earth, or another celestial body. It is an angular measurement, usually expressed in degrees and denoted by the Greek lette ...
in radians, and
: is the Schwarzschild radius
The Schwarzschild radius or the gravitational radius is a physical parameter in the Schwarzschild solution to Einstein's field equations that corresponds to the radius defining the event horizon of a Schwarzschild black hole. It is a characteris ...
of the massive body (in meters), which is related to its mass by
::
: where is the gravitational constant. The classical Newtonian theory of gravity is recovered in the limit as the ratio goes to zero. In that limit, the metric returns to that defined by special relativity
In physics, the special theory of relativity, or special relativity for short, is a scientific theory regarding the relationship between space and time. In Albert Einstein's original treatment, the theory is based on two postulates:
# The laws ...
.
In practice, this ratio is almost always extremely small. For example, the Schwarzschild radius of the Earth is roughly 9 mm ( inch); at the surface of the Earth, the corrections to Newtonian gravity are only one part in a billion. The Schwarzschild radius of the Sun is much larger, roughly 2953 meters, but at its surface, the ratio is roughly 4 parts in a million. A white dwarf
A white dwarf is a stellar core remnant composed mostly of electron-degenerate matter. A white dwarf is very dense: its mass is comparable to the Sun's, while its volume is comparable to the Earth's. A white dwarf's faint luminosity comes ...
star is much denser, but even here the ratio at its surface is roughly 250 parts in a million. The ratio only becomes large close to ultra-dense objects such as neutron star
A neutron star is the collapsed core of a massive supergiant star, which had a total mass of between 10 and 25 solar masses, possibly more if the star was especially metal-rich. Except for black holes and some hypothetical objects (e.g. w ...
s (where the ratio is roughly 50%) and black holes.
Orbits of test particles
 We may simplify the problem by using symmetry to eliminate one variable from consideration. Since the Schwarzschild metric is symmetrical about , any geodesic that begins moving in that plane will remain in that plane indefinitely (the plane is
We may simplify the problem by using symmetry to eliminate one variable from consideration. Since the Schwarzschild metric is symmetrical about , any geodesic that begins moving in that plane will remain in that plane indefinitely (the plane is totally geodesic
This is a glossary of some terms used in Riemannian geometry and metric geometry — it doesn't cover the terminology of differential topology.
The following articles may also be useful; they either contain specialised vocabulary or provi ...
). Therefore, we orient the coordinate system so that the orbit of the particle lies in that plane, and fix the coordinate to be so that the metric (of this plane) simplifies to
:
Two constants of motion In mechanics, a constant of motion is a quantity that is conserved throughout the motion, imposing in effect a constraint on the motion. However, it is a ''mathematical'' constraint, the natural consequence of the equations of motion, rather than ...
(values that do not change over proper time ) can be identified (cf. the derivation given below). One is the total energy :
:
and the other is the specific angular momentum
In celestial mechanics, the specific relative angular momentum (often denoted \vec or \mathbf) of a body is the angular momentum of that body divided by its mass. In the case of two orbiting bodies it is the vector product of their relative posit ...
:
:
where is the total angular momentum of the two bodies, and is the reduced mass
In physics, the reduced mass is the "effective" inertial mass appearing in the two-body problem of Newtonian mechanics. It is a quantity which allows the two-body problem to be solved as if it were a one-body problem. Note, however, that the mass ...
. When , the reduced mass is approximately equal to . Sometimes it is assumed that . In the case of the planet Mercury this simplification introduces an error more than twice as large as the relativistic effect. When discussing geodesics, can be considered fictitious, and what matters are the constants and . In order to cover all possible geodesics, we need to consider cases in which is infinite (giving trajectories of photon
A photon () is an elementary particle that is a quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves, and the force carrier for the electromagnetic force. Photons are massless, so they a ...
s) or imaginary (for tachyonic
A tachyon () or tachyonic particle is a hypothetical particle that always travels faster than light. Physicists believe that faster-than-light particles cannot exist because they are not consistent with the known laws of physics. If such part ...
geodesics). For the photonic case, we also need to specify a number corresponding to the ratio of the two constants, namely , which may be zero or a non-zero real number.
Substituting these constants into the definition of the Schwarzschild metric
:
yields an equation of motion for the radius as a function of the proper time :
:
The formal solution to this is
:
Note that the square root will be imaginary for tachyonic geodesics.
Using the relation higher up between and , we can also write
:
Since asymptotically the integrand is inversely proportional to , this shows that in the frame of reference if approaches it does so exponentially without ever reaching it. However, as a function of , does reach .
The above solutions are valid while the integrand is finite, but a total solution may involve two or an infinity of pieces, each described by the integral but with alternating signs for the square root.
When and , we can solve for and explicitly:
:
and for photonic geodesics () with zero angular momentum
:
(Although the proper time is trivial in the photonic case, one can define an affine parameter , and then the solution to the geodesic equation is .)
Another solvable case is that in which and and are constant. In the volume where this gives for the proper time
:
This is close to solutions with small and positive. Outside of the solution is tachyonic and the "proper time" is space-like:
:
This is close to other tachyonic solutions with small and negative. The constant tachyonic geodesic outside is not continued by a constant geodesic inside , but rather continues into a "parallel exterior region" (see Kruskal–Szekeres coordinates
In general relativity, Kruskal–Szekeres coordinates, named after Martin Kruskal and George Szekeres, are a coordinate system for the Schwarzschild geometry for a black hole. These coordinates have the advantage that they cover the entire space ...
). Other tachyonic solutions can enter a black hole and re-exit into the parallel exterior region. The constant solution inside the event horizon () is continued by a constant solution in a white hole
In general relativity, a white hole is a hypothetical region of spacetime and singularity that cannot be entered from the outside, although energy-matter, light and information can escape from it. In this sense, it is the reverse of a black ho ...
.
When the angular momentum is not zero we can replace the dependence on proper time by a dependence on the angle using the definition of
:
which yields the equation for the orbit
:
where, for brevity, two length-scales, and , have been defined by
:
Note that in the tachyonic case, will be imaginary and real or infinite.
The same equation can also be derived using a Lagrangian approach or the Hamilton–Jacobi equation
In physics, the Hamilton–Jacobi equation, named after William Rowan Hamilton and Carl Gustav Jacob Jacobi, is an alternative formulation of classical mechanics, equivalent to other formulations such as Newton's laws of motion, Lagrangian mecha ...
Landau and Lifshitz (1975), pp. 306–309. (see below). The solution of the orbit equation is
:
This can be expressed in terms of the Weierstrass elliptic function
In mathematics, the Weierstrass elliptic functions are elliptic functions that take a particularly simple form. They are named for Karl Weierstrass. This class of functions are also referred to as ℘-functions and they are usually denoted by t ...
.
Local and delayed velocities
Unlike in classical mechanics, in Schwarzschild coordinates and are not the radial and transverse components of the localvelocity
Velocity is the directional speed of an object in motion as an indication of its rate of change in position as observed from a particular frame of reference and as measured by a particular standard of time (e.g. northbound). Velocity i ...
(relative to a stationary observer), instead they give the components for the celerity which are related to by
:
for the radial and
:
for the transverse component of motion, with . The coordinate bookkeeper far away from the scene observes the shapiro-delayed velocity , which is given by the relation
: and .
The time dilation factor between the bookkeeper and the moving test-particle can also be put into the form
:
where the numerator is the gravitational, and the denominator is the kinematic component of the time dilation. For a particle falling in from infinity the left factor equals the right factor, since the in-falling velocity matches the escape velocity in this case.
The two constants angular momentum and total energy of a test-particle with mass are in terms of
:
and
:
where
:
and
:
For massive testparticles is the Lorentz factor
The Lorentz factor or Lorentz term is a quantity expressing how much the measurements of time, length, and other physical properties change for an object while that object is moving. The expression appears in several equations in special relativit ...
and is the proper time, while for massless particles like photons is set to and takes the role of an affine parameter. If the particle is massless is replaced with and with , where is the Planck constant
The Planck constant, or Planck's constant, is a fundamental physical constant of foundational importance in quantum mechanics. The constant gives the relationship between the energy of a photon and its frequency, and by the mass-energy equivale ...
and the locally observed frequency.
Exact solution using elliptic functions
The fundamental equation of the orbit is easier to solveThis substitution of for is also common in classical central-force problems, since it also renders those equations easier to solve. For further information, please see the article on the classical central-force problem. if it is expressed in terms of the inverse radius : The right-hand side of this equation is acubic polynomial
In mathematics, a cubic function is a function of the form f(x)=ax^3+bx^2+cx+d
where the coefficients , , , and are complex numbers, and the variable takes real values, and a\neq 0. In other words, it is both a polynomial function of degree ...
, which has three roots
A root is the part of a plant, generally underground, that anchors the plant body, and absorbs and stores water and nutrients.
Root or roots may also refer to:
Art, entertainment, and media
* ''The Root'' (magazine), an online magazine focusing ...
, denoted here as , , and
:
The sum of the three roots equals the coefficient of the term
:
A cubic polynomial with real coefficients can either have three real roots, or one real root and two complex conjugate
In mathematics, the complex conjugate of a complex number is the number with an equal real part and an imaginary part equal in magnitude but opposite in sign. That is, (if a and b are real, then) the complex conjugate of a + bi is equal to a - ...
roots. If all three roots are real number
In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every ...
s, the roots are labeled so that . If instead there is only one real root, then that is denoted as ; the complex conjugate roots are labeled and . Using Descartes' rule of signs
In mathematics, Descartes' rule of signs, first described by René Descartes in his work ''La Géométrie'', is a technique for getting information on the number of positive real roots of a polynomial. It asserts that the number of positive roots i ...
, there can be at most one negative root; is negative if and only if . As discussed below, the roots are useful in determining the types of possible orbits.
Given this labeling of the roots, the solution of the fundamental orbital equation is
:
where represents the function (one of the Jacobi elliptic function In mathematics, the Jacobi elliptic functions are a set of basic elliptic functions. They are found in the description of the motion of a pendulum (see also pendulum (mathematics)), as well as in the design of electronic elliptic filters. While tri ...
s) and is a constant of integration reflecting the initial position. The elliptic modulus
In mathematics, the modular lambda function λ(τ)\lambda(\tau) is not a modular function (per the Wikipedia definition), but every modular function is a rational function in \lambda(\tau). Some authors use a non-equivalent definition of "modular f ...
of this elliptic function is given by the formula
:
Newtonian limit
To recover the Newtonian solution for the planetary orbits, one takes the limit as the Schwarzschild radius goes to zero. In this case, the third root becomes roughly , and much larger than or . Therefore, the modulus tends to zero; in that limit, becomes the trigonometric sine function : Consistent with Newton's solutions for planetary motions, this formula describes a focal conic of eccentricity : If is a positive real number, then the orbit is an ellipse where and represent the distances of furthest and closest approach, respectively. If is zero or a negative real number, the orbit is aparabola
In mathematics, a parabola is a plane curve which is Reflection symmetry, mirror-symmetrical and is approximately U-shaped. It fits several superficially different Mathematics, mathematical descriptions, which can all be proved to define exact ...
or a hyperbola
In mathematics, a hyperbola (; pl. hyperbolas or hyperbolae ; adj. hyperbolic ) is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, ca ...
, respectively. In these latter two cases, represents the distance of closest approach; since the orbit goes to infinity (), there is no distance of furthest approach.
Roots and overview of possible orbits
A root represents a point of the orbit where the derivative vanishes, i.e., where . At such a turning point, reaches a maximum, a minimum, or an inflection point, depending on the value of the second derivative, which is given by the formula : If all three roots are distinct real numbers, the second derivative is positive, negative, and positive at ''u''1, ''u''2, and ''u''3, respectively. It follows that a graph of ''u'' versus φ may either oscillate between ''u''1 and ''u''2, or it may move away from ''u''3 towards infinity (which corresponds to ''r'' going to zero). If ''u''1 is negative, only part of an "oscillation" will actually occur. This corresponds to the particle coming from infinity, getting near the central mass, and then moving away again toward infinity, like the hyperbolic trajectory in the classical solution. If the particle has just the right amount of energy for its angular momentum, ''u''2 and ''u''3 will merge. There are three solutions in this case. The orbit may spiral in to , approaching that radius as (asymptotically) a decreasing exponential in φ, , or . Or one can have a circular orbit at that radius. Or one can have an orbit that spirals down from that radius to the central point. The radius in question is called the inner radius and is between and 3 times ''rs''. A circular orbit also results when is equal to , and this is called the outer radius. These different types of orbits are discussed below. If the particle comes at the central mass with sufficient energy and sufficiently low angular momentum then only will be real. This corresponds to the particle falling into a black hole. The orbit spirals in with a finite change in φ.Precession of orbits
The function sn and its square sn2 have periods of 4''K'' and 2''K'', respectively, where ''K'' is defined by the equationIn the mathematical literature, ''K'' is known as the complete elliptic integral of the first kind; for further information, please see the article onelliptic integral
In integral calculus, an elliptic integral is one of a number of related functions defined as the value of certain integrals, which were first studied by Giulio Fagnano and Leonhard Euler (). Their name originates from their originally arising in ...
s.
:
Therefore, the change in φ over one oscillation of (or, equivalently, one oscillation of ) equals
:
In the classical limit, ''u''3 approaches and is much larger than or . Hence, is approximately
:
For the same reasons, the denominator of Δφ is approximately
:
Since the modulus is close to zero, the period ''K'' can be expanded in powers of ; to lowest order, this expansion yields
:
Substituting these approximations into the formula for Δφ yields a formula for angular advance per radial oscillation
:
For an elliptical orbit, and represent the inverses of the longest and shortest distances, respectively. These can be expressed in terms of the ellipse's semi-major axis and its orbital eccentricity ,
:
giving
:
Substituting the definition of gives the final equation
:
Bending of light by gravity
impact parameter
In physics, the impact parameter is defined as the perpendicular distance between the path of a projectile and the center of a potential field created by an object that the projectile is approaching (see diagram). It is often referred to in ...
, somewhat greater than the distance of closest approach
The distance of closest approach of two objects is the distance between their centers when they are externally tangent. The objects may be geometric shapes or physical particles with well-defined boundaries. The distance of closest approach is ...
, :
Although this formula is approximate, it is accurate for most measurements of gravitational lensing
A gravitational lens is a distribution of matter (such as a cluster of galaxies) between a distant light source and an observer that is capable of bending the light from the source as the light travels toward the observer. This effect is known ...
, due to the smallness of the ratio . For light grazing the surface of the sun, the approximate angular deflection is roughly 1.75 arcseconds
A minute of arc, arcminute (arcmin), arc minute, or minute arc, denoted by the symbol , is a unit of angular measurement equal to of one degree. Since one degree is of a turn (or complete rotation), one minute of arc is of a turn. The ...
, roughly one millionth part of a circle.
Relation to Newtonian physics
Effective radial potential energy
The equation of motion for the particle derived above : can be rewritten using the definition of theSchwarzschild radius
The Schwarzschild radius or the gravitational radius is a physical parameter in the Schwarzschild solution to Einstein's field equations that corresponds to the radius defining the event horizon of a Schwarzschild black hole. It is a characteris ...
''r''s as
:
which is equivalent to a particle moving in a one-dimensional effective potential
:
The first two terms are well-known classical energies, the first being the attractive Newtonian gravitational potential energy and the second corresponding to the repulsive "centrifugal" potential energy; however, the third term is an attractive energy unique to general relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics ...
. As shown below and elsewhere, this inverse-cubic energy causes elliptical orbits to precess gradually by an angle δφ per revolution
:
where is the semi-major axis and is the eccentricity.
The third term is attractive and dominates at small values, giving a critical inner radius ''r''inner at which a particle is drawn inexorably inwards to ; this inner radius is a function of the particle's angular momentum per unit mass or, equivalently, the length-scale defined above.
Circular orbits and their stability
quadratic formula
In elementary algebra, the quadratic formula is a formula that provides the solution(s) to a quadratic equation. There are other ways of solving a quadratic equation instead of using the quadratic formula, such as factoring (direct factoring, g ...
. The inner radius ''r''inner is unstable, because the attractive third force strengthens much faster than the other two forces when ''r'' becomes small; if the particle slips slightly inwards from ''r''inner (where all three forces are in balance), the third force dominates the other two and draws the particle inexorably inwards to ''r'' = 0. At the outer radius, however, the circular orbits are stable; the third term is less important and the system behaves more like the non-relativistic Kepler problem
In classical mechanics, the Kepler problem is a special case of the two-body problem, in which the two bodies interact by a central force ''F'' that varies in strength as the inverse square of the distance ''r'' between them. The force may be ei ...
.
When is much greater than (the classical case), these formulae become approximately
:
centrifugal force
In Newtonian mechanics, the centrifugal force is an inertial force (also called a "fictitious" or "pseudo" force) that appears to act on all objects when viewed in a rotating frame of reference. It is directed away from an axis which is parall ...
equal to the Newtonian gravitational force:
:
Where is the reduced mass
In physics, the reduced mass is the "effective" inertial mass appearing in the two-body problem of Newtonian mechanics. It is a quantity which allows the two-body problem to be solved as if it were a one-body problem. Note, however, that the mass ...
.
In our notation, the classical orbital angular speed equals
:
At the other extreme, when ''a''2 approaches 3''r''s2 from above, the two radii converge to a single value
:
The quadratic solutions above ensure that ''r''outer is always greater than 3''r''s, whereas ''r''inner lies between ''r''s and 3''r''s. Circular orbits smaller than ''r''s are not possible. For massless particles, ''a'' goes to infinity, implying that there is a circular orbit for photons at ''r''inner = ''r''s. The sphere of this radius is sometimes known as the photon sphere
A photon sphere or photon circle is an area or region of space where gravity is so strong that photons are forced to travel in orbits, which is also sometimes called the last photon orbit. The radius of the photon sphere, which is also the lower ...
.
Precession of elliptical orbits
Taylor series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor ser ...
expansion yields
:
Multiplying by the period ''T'' of one revolution gives the precession of the orbit per revolution
:
where we have used ''ωφT'' = 2''п'' and the definition of the length-scale ''a''. Substituting the definition of the Schwarzschild radius
The Schwarzschild radius or the gravitational radius is a physical parameter in the Schwarzschild solution to Einstein's field equations that corresponds to the radius defining the event horizon of a Schwarzschild black hole. It is a characteris ...
''r''s gives
:
This may be simplified using the elliptical orbit's semiaxis ''A'' and eccentricity ''e'' related by the formula
:
to give the precession angle
:
Mathematical derivations of the orbital equation
Christoffel symbols
The non-vanishingChristoffel symbols
In mathematics and physics, the Christoffel symbols are an array of numbers describing a metric connection. The metric connection is a specialization of the affine connection to surfaces or other manifolds endowed with a metric, allowing distanc ...
for the Schwarzschild-metric are:
:
Geodesic equation
According to Einstein's theory of general relativity, particles of negligible mass travel along geodesics in the space-time. In flat space-time, far from a source of gravity, these geodesics correspond to straight lines; however, they may deviate from straight lines when the space-time is curved. The equation for the geodesic lines is : where Γ represents theChristoffel symbol
In mathematics and physics, the Christoffel symbols are an array of numbers describing a metric connection. The metric connection is a specialization of the affine connection to surfaces or other manifolds endowed with a metric, allowing dist ...
and the variable parametrizes the particle's path through space-time, its so-called world line
The world line (or worldline) of an object is the path that an object traces in 4-dimensional spacetime. It is an important concept in modern physics, and particularly theoretical physics.
The concept of a "world line" is distinguished from c ...
. The Christoffel symbol depends only on the metric tensor , or rather on how it changes with position. The variable is a constant multiple of the proper time
In relativity, proper time (from Latin, meaning ''own time'') along a timelike world line is defined as the time as measured by a clock following that line. It is thus independent of coordinates, and is a Lorentz scalar. The proper time interval ...
for timelike orbits (which are traveled by massive particles), and is usually taken to be equal to it. For lightlike (or null) orbits (which are traveled by massless particles such as the photon
A photon () is an elementary particle that is a quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves, and the force carrier for the electromagnetic force. Photons are massless, so they a ...
), the proper time is zero and, strictly speaking, cannot be used as the variable . Nevertheless, lightlike orbits can be derived as the ultrarelativistic limit
In physics, a particle is called ultrarelativistic when its speed is very close to the speed of light .
The expression for the relativistic energy of a particle with rest mass and momentum is given by
:E^2 = m^2 c^4 + p^2 c^2.
The energy of ...
of timelike orbits, that is, the limit as the particle mass ''m'' goes to zero while holding its total energy
In physics, energy (from Ancient Greek: ἐνέργεια, ''enérgeia'', “activity”) is the quantitative property that is transferred to a body or to a physical system, recognizable in the performance of work and in the form of hea ...
fixed.
Therefore, to solve for the motion of a particle, the most straightforward way is to solve the geodesic equation, an approach adopted by Einstein and others. The Schwarzschild metric may be written as
:
where the two functions and its reciprocal are defined for brevity. From this metric, the Christoffel symbols may be calculated, and the results substituted into the geodesic equations
:
It may be verified that is a valid solution by substitution into the first of these four equations. By symmetry, the orbit must be planar, and we are free to arrange the coordinate frame so that the equatorial plane is the plane of the orbit. This solution simplifies the second and fourth equations.
To solve the second and third equations, it suffices to divide them by and , respectively.
:
which yields two constants of motion.
Lagrangian approach
Because test particles follow geodesics in a fixed metric, the orbits of those particles may be determined using the calculus of variations, also called the Lagrangian approach. Geodesics in space-time are defined as curves for which small local variations in their coordinates (while holding their endpoints events fixed) make no significant change in their overall length ''s''. This may be expressed mathematically using the calculus of variations : where ''τ'' is theproper time
In relativity, proper time (from Latin, meaning ''own time'') along a timelike world line is defined as the time as measured by a clock following that line. It is thus independent of coordinates, and is a Lorentz scalar. The proper time interval ...
, ''s'' = ''cτ'' is the arc-length in space-time and ''T'' is defined as
:
in analogy with kinetic energy
In physics, the kinetic energy of an object is the energy that it possesses due to its motion.
It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acc ...
. If the derivative with respect to proper time is represented by a dot for brevity
:
''T'' may be written as
:
Constant factors (such as ''c'' or the square root of two) don't affect the answer to the variational problem; therefore, taking the variation inside the integral yields Hamilton's principle
In physics, Hamilton's principle is William Rowan Hamilton's formulation of the principle of stationary action. It states that the dynamics of a physical system are determined by a variational problem for a functional based on a single function, ...
:
The solution of the variational problem is given by Lagrange's equations
In physics, Lagrangian mechanics is a formulation of classical mechanics founded on the stationary-action principle (also known as the principle of least action). It was introduced by the Italian-French mathematician and astronomer Joseph-Lo ...
:
When applied to ''t'' and ''φ'', these equations reveal two constants of motion In mechanics, a constant of motion is a quantity that is conserved throughout the motion, imposing in effect a constraint on the motion. However, it is a ''mathematical'' constraint, the natural consequence of the equations of motion, rather than ...
:
which may be expressed in terms of two constant length-scales, and
:
As shown above, substitution of these equations into the definition of the Schwarzschild metric yields the equation for the orbit.
Hamiltonian approach
A Lagrangian solution can be recast into an equivalent Hamiltonian form. In this case, the Hamiltonian is given by : Once again, the orbit may be restricted to by symmetry. Since and do not appear in the Hamiltonian, their conjugate momenta are constant; they may be expressed in terms of the speed of light and two constant length-scales and : The derivatives with respect to proper time are given by : Dividing the first equation by the second yields the orbital equation : The radial momentum ''p''''r'' can be expressed in terms of ''r'' using the constancy of the Hamiltonian ; this yields the fundamental orbital equation :Hamilton–Jacobi approach
general relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics ...
, through Fermat's principle
Fermat's principle, also known as the principle of least time, is the link between ray optics and wave optics. In its original "strong" form, Fermat's principle states that the path taken by a ray between two given points is the pat ...
. The basic idea is that, due to gravitational slowing of time, parts of a wave-front closer to a gravitating mass move more slowly than those further away, thus bending the direction of the wave-front's propagation.
Using general covariance, the Hamilton–Jacobi equation for a single particle of unit mass can be expressed in arbitrary coordinates as
:
This is equivalent to the Hamiltonian formulation above, with the partial derivatives of the action taking the place of the generalized momenta. Using the Schwarzschild metric ''g''μν, this equation becomes
:
where we again orient the spherical coordinate system with the plane of the orbit. The time ''t'' and azimuthal angle ''φ'' are cyclic coordinates, so that the solution for Hamilton's principal function ''S'' can be written
:
where and are the constant generalized momenta. The Hamilton–Jacobi equation gives an integral solution for the radial part
:
Taking the derivative of Hamilton's principal function ''S'' with respect to the conserved momentum ''p''φ yields
:
which equals
:
Taking an infinitesimal variation in φ and ''r'' yields the fundamental orbital equation
:
where the conserved length-scales ''a'' and ''b'' are defined by the conserved momenta by the equations
:
Hamilton's principle
Theaction
Action may refer to:
* Action (narrative), a literary mode
* Action fiction, a type of genre fiction
* Action game, a genre of video game
Film
* Action film, a genre of film
* ''Action'' (1921 film), a film by John Ford
* ''Action'' (1980 fil ...
integral for a particle affected only by gravity is
:
where is the proper time
In relativity, proper time (from Latin, meaning ''own time'') along a timelike world line is defined as the time as measured by a clock following that line. It is thus independent of coordinates, and is a Lorentz scalar. The proper time interval ...
and is any smooth parameterization of the particle's world line. If one applies the calculus of variations to this, one again gets the equations for a geodesic. To simplify the calculations, one first takes the variation of the square of the integrand. For the metric and coordinates of this case and assuming that the particle is moving in the equatorial plane , that square is
:
Taking variation of this gives
:
Motion in longitude
Vary with respect to longitude only to get : Divide by to get the variation of the integrand itself : Thus : Integrating by parts gives : The variation of the longitude is assumed to be zero at the end points, so the first term disappears. The integral can be made nonzero by a perverse choice of unless the other factor inside is zero everywhere. So the equation of motion is :Motion in time
Vary with respect to time only to get : Divide by to get the variation of the integrand itself : Thus : Integrating by parts gives : So the equation of motion is :Conserved momenta
Integrate these equations of motion to determine the constants of integration getting : These two equations for the constants of motion (angular momentum) and (energy) can be combined to form one equation that is true even forphoton
A photon () is an elementary particle that is a quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves, and the force carrier for the electromagnetic force. Photons are massless, so they a ...
s and other massless particles for which the proper time
In relativity, proper time (from Latin, meaning ''own time'') along a timelike world line is defined as the time as measured by a clock following that line. It is thus independent of coordinates, and is a Lorentz scalar. The proper time interval ...
along a geodesic is zero.
:
Radial motion
Substituting : and : into the metric equation (and using ) gives : from which one can derive : which is the equation of motion for . The dependence of on can be found by dividing this by : to get : which is true even for particles without mass. If length scales are defined by : and : then the dependence of on simplifies to :See also
*Kepler problem
In classical mechanics, the Kepler problem is a special case of the two-body problem, in which the two bodies interact by a central force ''F'' that varies in strength as the inverse square of the distance ''r'' between them. The force may be ei ...
* Classical central-force problem
* Two-body problem in general relativity
* Frame fields in general relativity
A frame field in general relativity (also called a tetrad or vierbein) is a set of four pointwise-orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime ...
Notes
References
Bibliography
* Schwarzschild, K. (1916). Über das Gravitationsfeld eines Massenpunktes nach der Einstein'schen Theorie. ''Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften'' 1, 189–196. *scan of the original paper
*
text of the original paper, in Wikisource
*
translation by Antoci and Loinger
*
a commentary on the paper, giving a simpler derivation
* Schwarzschild, K. (1916). Über das Gravitationsfeld einer Kugel aus inkompressibler Flüssigkeit. ''Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften'' 1, 424-?. * * * * * * * (See
Gravitation (book)
''Gravitation'' is a widely adopted textbook on Albert Einstein's general theory of relativity, written by Charles W. Misner, Kip S. Thorne, and John Archibald Wheeler. It was originally published by W. H. Freeman and Company in 1973 and repr ...
.)
*
*
*
*
*
*
*
*
* {{cite book , last = Whittaker , first = ET , author-link = E. T. Whittaker , year = 1937 , title = A Treatise on the Analytical Dynamics of Particles and Rigid Bodies, with an Introduction to the Problem of Three Bodies , edition = 4th , publisher = Dover Publications , location = New York , pages 389
ndash;393 , isbn = 978-1-114-28944-4
External links
from ''Reflections on Relativity'' by Kevin Brown. Exact solutions in general relativity