Generalized Rabi Frequency

The Rabi frequency is the frequency at which the probability amplitudes of two atomic energy levels fluctuate in an oscillating electromagnetic field. It is proportional to the Transition Dipole Moment of the two levels and to the amplitude (''not'' intensity) of the Electromagnetic field. Population transfer between the levels of such a 2-level system illuminated with light exactly resonant with the difference in energy between the two levels will occur at the Rabi frequency; when the incident light is detuned from this energy difference (detuned from resonance) then the population transfer occurs at the generalized Rabi frequency. The Rabi frequency is a semiclassical concept since it treats the atom as an object with quantized energy levels and the electromagnetic field as a continuous wave.

In the context of a nuclear magnetic resonance experiment, the Rabi frequency is the nutation frequency of a sample's net nuclear magnetization vector about a radio-frequency field. (Note that this is distinct from the Larmor frequency, which characterizes the precession of a transverse nuclear magnetization about a static magnetic field.)

Derivation

Consider two energy eigenstates of a quantum system with Hamiltonian $\hat_0$ (for example, this could be the Hamiltonian of a particle in a $\frac$ potential, like the Hydrogen atom or the Alkali atoms):

$\begin \psi_1(\mathbf, t) &= e^ , 1\rangle\\ \psi_2(\mathbf, t) &= e^ , 2\rangle \end$

We want to consider the time dependent Hamiltonian

$\hat = \hat_0 + \hat(t)$

where $\hat(t) = e\mathbf \cdot \mathbf_0 \cos(\omega t)$ is the potential of the electromagnetic field. Treating the potential as a perturbation, we can expect the eigenstates of the perturbed Hamiltonian to be some mixture of the eigenstates of the original Hamiltonian with time dependent coefficients:

$\Psi(\mathbf, t) = c_1(t) e^ , 1\rangle + c_2(t) e^ , 2\rangle$

Plugging this into the time dependent Schrödinger equation

$i\hbar \frac = \hat \Psi(\mathbf, t)$

taking the inner product with each of $e^\langle 1,$ and $e^\langle 2,$, and using the orthogonality condition of eigenstates $\langle i , j \rangle = \delta_$, we arrive at two equations in the coefficients $c_1(t)$ and $c_2(t)$:

$\begin i \dot_1(t) &= \frac (\langle 1, e\mathbf \cdot \mathbf_0 , 1 \rangle + e^ \langle 1, e\mathbf \cdot \mathbf_0 , 2 \rangle ) \\ i \dot_2(t) &= \frac (e^\langle 2, e\mathbf \cdot \mathbf_0 , 1 \rangle + \langle 1, e\mathbf \cdot \mathbf_0 , 1 \rangle ) \end$

where $\omega_0 = \omega_2 - \omega_1$. The two terms in parentheses are dipole matrix elements dotted into the polarization vector of the electromagnetic field. In considering the spherically symmetric spatial eigenfunctions $, i\rangle$ of the Hydrogen atom potential, the diagonal matrix elements go to zero, leaving us with

$\begin i \dot_1(t) &= \frac \langle 1, e\mathbf \cdot \mathbf_0 , 2 \rangle e^ \\ i \dot_2(t) &= \frac \langle 2, e\mathbf \cdot \mathbf_0 , 1 \rangle e^ \end$

or

$\begin i \dot_1(t) &= \Omega c_2(t) \cos(\omega t) e^ \\ i \dot_2(t) &= \Omega^* c_1(t) \cos(\omega t) e^ \end$

Here, $\Omega_ = \frac$ is the Rabi Frequency.

Intuition

In the numerator we have the transition dipole moment for the $i \to j$ transition, whose squared amplitude represents the strength of the interaction between the electromagnetic field and the atom, and $\mathbf_0 = \hat E_0$ is the vector electric field amplitude, which includes the polarization. The numerator has dimensions of energy, so dividing by $\hbar$ gives an angular frequency.

By analogy with a classical dipole, it is clear that an atom with a large dipole moment will be more susceptible to perturbation by an electric field. The dot product includes a factor of $\cos\theta$, where $\theta$ is the angle between the polarization of the light and the transition dipole moment. When they are parallel the interaction is strongest, when they are perpendicular there is no interaction at all.

If we rewrite the differential equations found above:

$\begin i \dot_1(t) = \Omega c_2(t) \cos(\omega t) e^ &\to \frac (e^ + e^)\\ i \dot_2(t) = \Omega^* c_1(t) \cos(\omega t) e^ &\to \frac (e^ + e^) \end$

and apply the Rotating-wave approximation, which assumes that $\omega + \omega_0 >> \omega - \omega_0$, such that we can discard the high frequency oscillating terms, we have

$\begin i \dot_1(t) &= \frac e^\\ i \dot_2(t) &= \frac e^ \end$

where $\delta = \omega - \omega_0$. We can solve these equations, assuming at time $t = 0$ the atom is in $, 1\rangle$ (i.e. $c_1(0) = 1$) to find

$, c_2(t), ^2 = \frac$

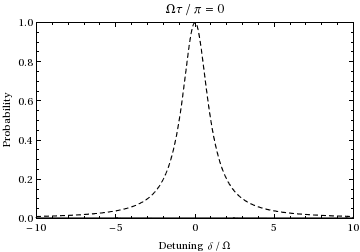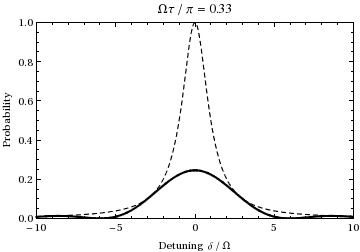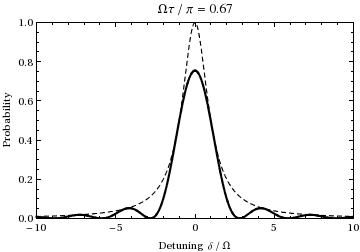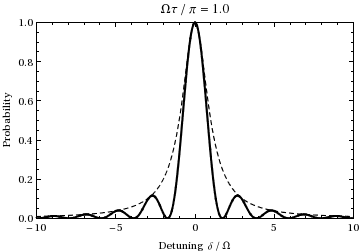
This is the probability as a function of detuning and time of the population of state $, 2 \rangle$. A plot as a function of detuning and ramping the time from 0 to $t = \frac$ gives:

We see that for $\delta = 0$ the population will oscillate between the two states at the Rabi frequency.

Generalized Rabi frequency

The quantity $\sqrt$ is commonly referred to as the "generalized Rabi frequency." For cases in which $\delta \neq 0$, Rabi flopping actually occurs at this frequency, where $\delta$ is the detuning, a measure of how far the light is off-resonance relative to the transition. For instance, examining the above animation at an offset frequency of ±1.73, one can see that during the 1/2 Rabi cycle (at resonance) shown during the animation, the oscillation instead undergoes one ''full'' cycle, thus at twice the (normal) Rabi frequency $\Omega_$, just as predicted by this equation. Also note that as the incident light frequency shifts further from the transition frequency, the amplitude of the Rabi oscillation decreases, as is illustrated by the dashed envelope in the above plot.

Two-Photon Rabi Frequency

Coherent Rabi oscillations may also be driven by two-photon transitions. In this case we consider a system with three atomic energy levels, $, 1\rangle$, $, i\rangle$, and $, 2\rangle$, where $, i\rangle$ represents a so-called intermediate state with corresponding frequency $\omega_i$, and an electromagnetic field with two frequency components:

$\hat(t) = e\mathbf \cdot \mathbf_ \cos(\omega_ t) + e\mathbf \cdot \mathbf_ \cos(\omega_ t)$

Now, $\omega_i$ may be much greater than both $\omega_1$ and $\omega_2$, or $\omega_2 > \omega_i > \omega_1$, as illustrated in the figure on the right.

A two-photon transition is ''not'' the same as excitation from the ground to intermediate state, and then out of the intermediate state to the excited state. Instead, the atom absorbs two photons simultaneously and is promoted directly between the initial and final states. There are two necessary conditions for this two-photon process (also known as a Raman process), to be the dominate model of the light-matter interaction:

$\begin \omega_ + \omega_ &= \omega_ - \omega_\\ \Delta = , \omega_ - \omega_, &>> 0 \end$

In words, the sum of the frequencies of the two photons must be on resonance with the transition between the initial and final states, and the individual frequencies of the photons must be detuned from the intermediate state to initial and final state transitions. If the latter condition is not met and $\Delta \to 0$, the dominate process will be one governed by rate equations in which the intermediate state is populated and stimulated and Spontaneous emission events from that state prevent the possibility of driving coherent oscillations between the initial and final states.

We may derive the two-photon Rabi frequency by returning to the equations

$\begin i \dot_1(t) &= \frac e^\\ i \dot_i(t) &= \frac e^ \end$

which now describe excitation between the ground and intermediate states. We know we have the solution

$c_i(t) = \frac$

where $\tilde_$ is the generalized Rabi frequency for the transition from the initial to intermediate state. Similarly for the intermediate to final state transition we have the equations

$\begin i \dot_i(t) &= \frac e^\\ i \dot_2(t) &= \frac e^ \end$

Now we plug $c_i(t)$ into the above equation for $\dot_2(t)$

$i \dot_2(t) = \frac e^$

Such that, upon solving this equation, we find the coefficient to be proportional to:

$c_2(t) \propto \frac$

This is the effective or two-photon Rabi frequency. It is the product of the individual Rabi frequencies for the $, 1\rangle \to , i\rangle$ and $, i\rangle \to , 2\rangle$ transitions, divided by the detuning from the intermediate state $, i\rangle$.

See also

* Rabi cycle
*Vacuum Rabi oscillation
* Rabi resonance method

References

{{reflist, 1

Quantum optics
Atomic physics
Atomic, molecular, and optical physics