Gabor–Wigner Transform on:
[Wikipedia]
[Google]
[Amazon]
The Gabor transform, named after
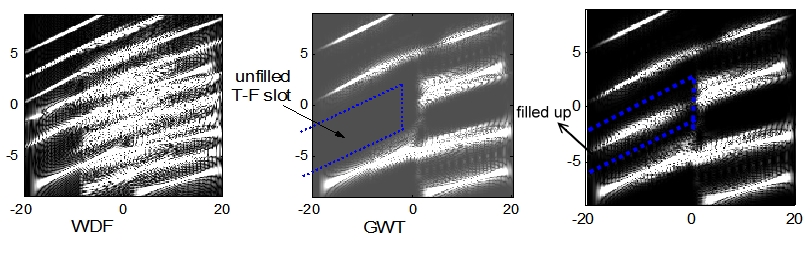 From the figure (WDF) above, it can also be observed that when using the Wigner transform (WDF), the generated cross-terms have a severe impact on modulation.
From the figure (WDF) above, it can also be observed that when using the Wigner transform (WDF), the generated cross-terms have a severe impact on modulation.
Dennis Gabor
Dennis Gabor ( ; ; 5 June 1900 – 9 February 1979) was a Hungarian-British physicist who received the Nobel Prize in Physics in 1971 for his invention of holography. He obtained British citizenship in 1946 and spent most of his life in Engla ...
, and the Wigner distribution function, named after Eugene Wigner
Eugene Paul Wigner (, ; November 17, 1902 – January 1, 1995) was a Hungarian-American theoretical physicist who also contributed to mathematical physics. He received the Nobel Prize in Physics in 1963 "for his contributions to the theory of th ...
, are both tools for time-frequency analysis. Since the Gabor transform
The Gabor transform, named after Dennis Gabor, is a special case of the short-time Fourier transform. It is used to determine the Sine wave, sinusoidal frequency and phase (waves), phase content of local sections of a signal as it changes over time ...
does not have high clarity, and the Wigner distribution function
The Wigner distribution function (WDF) is used in signal processing as a transform in time-frequency analysis.
The WDF was first proposed in physics to account for quantum corrections to classical statistical mechanics in 1932 by Eugene Wigner, ...
has a "cross term problem" (i.e. is non-linear), a 2007 study by S. C. Pei and J. J. Ding proposed a new combination of the two transforms that has high clarity and no cross term problem.S. C. Pei and J. J. Ding, “Relations between Gabor transforms and fractional Fourier transforms and their applications for signal processing,” IEEE Trans. Signal Process., vol. 55, no. 10, pp. 4839–4850, Oct. 2007.
Since the cross term does not appear in the Gabor transform, the time frequency distribution of the Gabor transform can be used as a filter to filter out the cross term in the output of the Wigner distribution function.
Mathematical definition
* Gabor transform : * Wigner distribution function : * Gabor–Wigner transform :There are many different combinations to define the Gabor–Wigner transform. Here four different definitions are given. # # # #Character
# Cross Term Problem: #: The definition of Wigner distribution function (WDF) is #: is the input signal, the time axis after transform, is the frequency axis after transform. #: If we design our input signal as : , and its WDF presents as below: #: #: and are called "auto-term", and other components are "cross-term", which is not the correct information from the original signal. #: The Gabor Transform (GT) can avoid the cross-term problem, while the Wigner-distribution function (WDF) has high clarity. By combining the two, the Gabor-Wigner Transform (GWT) achieves both high clarity and the ability to avoid the cross-term problem. Example are shown in the picture below. #: # Rotation relation: #: The GWT has rotation relation with the FRFT, making it useful for filter design, sampling, and multiplexing in the FRFT domain.Application
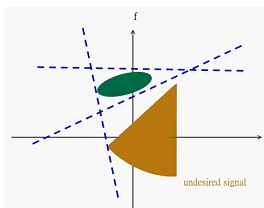
The Gabor–Wigner transform performs well in image processing, filter design, signal sampling, modulation, demodulation, speech processing, and biomedical engineering.Filter Design
The goal of filter design is to remove unwanted portions of the signal while preserving the necessary parts. By using the Gabor–Wigner transform, we can simultaneously consider filters in both the time domain and frequency domain, representing a form of time-frequency analysis. The main concept is illustrated as follows.
Signal Modulation
The purpose of modulation is to place a signal within a specific time or frequency range. Using the Gabor–Wigner transform, we can simultaneously consider how to introduce more or more suitable signal patterns in both the time and frequency domains. Due to the absence of cross-term issues, it performs better than the Wigner transform. From the figure (WDF) above, it can also be observed that when using the Wigner transform (WDF), the generated cross-terms have a severe impact on modulation.
From the figure (WDF) above, it can also be observed that when using the Wigner transform (WDF), the generated cross-terms have a severe impact on modulation.
Technique for fast implementation of the Gabor-Wigner Transform
# Due to the lower complexity of the Gabor transform compared to the Wigner transform, the Gabor transform is usually prioritized for calculation. When calculating the Wigner transform, it is only necessary to compute the Gabor transform in non-zero regions, as the values in other regions approach zero. Mathematically, this can be expressed as #: # When is a real function, for the Gabor transform, . This allows for a significant reduction in the required memory area when designing memory.Comparison
See also
* Time-frequency representation *Short-time Fourier transform
The short-time Fourier transform (STFT) is a Fourier-related transform used to determine the sinusoidal frequency and phase content of local sections of a signal as it changes over time. In practice, the procedure for computing STFTs is to divide ...
* Gabor transform
The Gabor transform, named after Dennis Gabor, is a special case of the short-time Fourier transform. It is used to determine the Sine wave, sinusoidal frequency and phase (waves), phase content of local sections of a signal as it changes over time ...
* Wigner distribution function
The Wigner distribution function (WDF) is used in signal processing as a transform in time-frequency analysis.
The WDF was first proposed in physics to account for quantum corrections to classical statistical mechanics in 1932 by Eugene Wigner, ...
References
{{DEFAULTSORT:Gabor-Wigner transform Integral transforms