Fuzzy Clustering on:
[Wikipedia]
[Google]
[Amazon]
Fuzzy clustering (also referred to as soft clustering or soft ''k''-means) is a form of clustering in which each
 This data set can be traditionally grouped into two clusters. By selecting a threshold on the x-axis, the data is separated into two clusters. The resulting clusters are labelled 'A' and 'B', as seen in the following image. Each point belonging to the data set would therefore have a membership coefficient of 1 or 0. This membership coefficient of each corresponding data point is represented by the inclusion of the y-axis.
This data set can be traditionally grouped into two clusters. By selecting a threshold on the x-axis, the data is separated into two clusters. The resulting clusters are labelled 'A' and 'B', as seen in the following image. Each point belonging to the data set would therefore have a membership coefficient of 1 or 0. This membership coefficient of each corresponding data point is represented by the inclusion of the y-axis.
 In fuzzy clustering, each data point can have membership to multiple clusters. By relaxing the definition of membership coefficients from strictly 1 or 0, these values can range from any value from 1 to 0. The following image shows the data set from the previous clustering, but now fuzzy c-means clustering is applied. First, a new threshold value defining two clusters may be generated. Next, new membership coefficients for each data point are generated based on clusters centroids, as well as distance from each cluster centroid.
In fuzzy clustering, each data point can have membership to multiple clusters. By relaxing the definition of membership coefficients from strictly 1 or 0, these values can range from any value from 1 to 0. The following image shows the data set from the previous clustering, but now fuzzy c-means clustering is applied. First, a new threshold value defining two clusters may be generated. Next, new membership coefficients for each data point are generated based on clusters centroids, as well as distance from each cluster centroid.
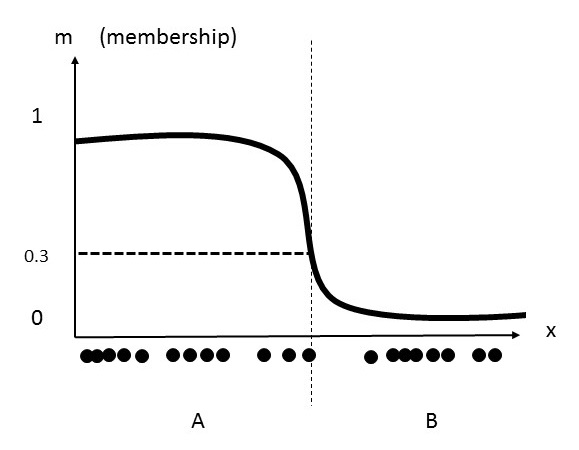 As one can see, the middle data point belongs to cluster A and cluster B. the value of 0.3 is this data point's membership coefficient for cluster A .
As one can see, the middle data point belongs to cluster A and cluster B. the value of 0.3 is this data point's membership coefficient for cluster A .

data point
In statistics, a unit of observation is the unit described by the data that one analyzes. A study may treat groups as a unit of observation with a country as the unit of analysis, drawing conclusions on group characteristics from data collected a ...
can belong to more than one cluster.
Clustering or cluster analysis
Cluster analysis or clustering is the task of grouping a set of objects in such a way that objects in the same group (called a cluster) are more similar (in some sense) to each other than to those in other groups (clusters). It is a main task of ...
involves assigning data points to clusters such that items in the same cluster are as similar as possible, while items belonging to different clusters are as dissimilar as possible. Clusters are identified via similarity measures. These similarity measures include distance, connectivity, and intensity. Different similarity measures may be chosen based on the data or the application.
Comparison to hard clustering
In non-fuzzy clustering (also known as hard clustering), data are divided into distinct clusters, where each data point can only belong to exactly one cluster. In fuzzy clustering, data points can potentially belong to multiple clusters. For example, an apple can be red or green (hard clustering), but an apple can also be red AND green (fuzzy clustering). Here, the apple can be red to a certain degree as well as green to a certain degree. Instead of the apple belonging to greenreen = 1
A rhyne (Somerset), rhine/rhyne (Gloucestershire), or reen (South Wales) (all pronounced "reen"; from Old English ''ryne'' or Welsh ''rhewyn'' or ''rhewin'' "ditch") is a term used in parts of England and Wales for a drainage ditch, or can ...
and not red ed = 0
Ed, ed or ED may refer to:
Arts and entertainment
* ''Ed'' (film), a 1996 film starring Matt LeBlanc
* Ed (''Fullmetal Alchemist'') or Edward Elric, a character in ''Fullmetal Alchemist'' media
* ''Ed'' (TV series), a TV series that ran fro ...
the apple can belong to green reen = 0.5and red ed = 0.5
Ed, ed or ED may refer to:
Arts and entertainment
* ''Ed'' (film), a 1996 film starring Matt LeBlanc
* Ed (''Fullmetal Alchemist'') or Edward Elric, a character in ''Fullmetal Alchemist'' media
* ''Ed'' (TV series), a TV series that ran fro ...
These value are normalized between 0 and 1; however, they do not represent probabilities, so the two values do not need to add up to 1.
Membership
Membership grades are assigned to each of the data points (tags). These membership grades indicate the degree to which data points belong to each cluster. Thus, points on the edge of a cluster, with lower membership grades, may be ''in the cluster'' to a lesser degree than points in the center of cluster.Fuzzy C-means clustering
One of the most widely used fuzzy clustering algorithms is the Fuzzy C-means clustering (FCM) algorithm.History
Fuzzy c-means (FCM) clustering was developed by J.C. Dunn in 1973, and improved by J.C. Bezdek in 1981.General description
The fuzzy ''c''-means algorithm is very similar to the ''k''-means algorithm: * Choose a number of clusters. * Assign coefficients randomly to each data point for being in the clusters. * Repeat until the algorithm has converged (that is, the coefficients' change between two iterations is no more than , the given sensitivity threshold) : ** Compute the centroid for each cluster (shown below). ** For each data point, compute its coefficients of being in the clusters.Centroid
Any point ''x'' has a set of coefficients giving the degree of being in the ''k''th cluster ''w''''k''(''x''). With fuzzy ''c''-means, the centroid of a cluster is the mean of all points, weighted by their degree of belonging to the cluster, or, mathematically, where ''m'' is the hyper- parameter that controls how fuzzy the cluster will be. The higher it is, the fuzzier the cluster will be in the end.Algorithm
The FCM algorithm attempts to partition a finite collection of elements into a collection of c fuzzy clusters with respect to some given criterion. Given a finite set of data, the algorithm returns a list of cluster centres and a partition matrix , where each element, , tells the degree to which element, , belongs to cluster . The FCM aims to minimize an objective function: :, where: :.Comparison to K-means clustering
K-means clustering also attempts to minimize the objective function shown above, except that in K-means, the membership values are either zero or one, and cannot take values in between, i.e. . In Fuzzy C-means, the degree of fuzziness is parametrized by , where a larger results in fuzzier clusters. In the limit , the memberships, , converge to 0 or 1, and the Fuzzy C-means objective coincides with that of K-means. In the absence of experimentation or domain knowledge, is commonly set to 2. The algorithm minimizes intra-cluster variance as well, but has the same problems as 'k'-means; the minimum is a local minimum, and the results depend on the initial choice of weights.Implementation
There are several implementations of this algorithm that are publicly available.Related algorithms
Fuzzy C-means (FCM) with automatically determined for the number of clusters could enhance the detection accuracy. Using a mixture of Gaussians along with the expectation-maximization algorithm is a more statistically formalized method which includes some of these ideas: partial membership in classes.Example
To better understand this principle, a classic example of mono-dimensional data is given below on an x axis. This data set can be traditionally grouped into two clusters. By selecting a threshold on the x-axis, the data is separated into two clusters. The resulting clusters are labelled 'A' and 'B', as seen in the following image. Each point belonging to the data set would therefore have a membership coefficient of 1 or 0. This membership coefficient of each corresponding data point is represented by the inclusion of the y-axis.
This data set can be traditionally grouped into two clusters. By selecting a threshold on the x-axis, the data is separated into two clusters. The resulting clusters are labelled 'A' and 'B', as seen in the following image. Each point belonging to the data set would therefore have a membership coefficient of 1 or 0. This membership coefficient of each corresponding data point is represented by the inclusion of the y-axis.
 In fuzzy clustering, each data point can have membership to multiple clusters. By relaxing the definition of membership coefficients from strictly 1 or 0, these values can range from any value from 1 to 0. The following image shows the data set from the previous clustering, but now fuzzy c-means clustering is applied. First, a new threshold value defining two clusters may be generated. Next, new membership coefficients for each data point are generated based on clusters centroids, as well as distance from each cluster centroid.
In fuzzy clustering, each data point can have membership to multiple clusters. By relaxing the definition of membership coefficients from strictly 1 or 0, these values can range from any value from 1 to 0. The following image shows the data set from the previous clustering, but now fuzzy c-means clustering is applied. First, a new threshold value defining two clusters may be generated. Next, new membership coefficients for each data point are generated based on clusters centroids, as well as distance from each cluster centroid.
 As one can see, the middle data point belongs to cluster A and cluster B. the value of 0.3 is this data point's membership coefficient for cluster A .
As one can see, the middle data point belongs to cluster A and cluster B. the value of 0.3 is this data point's membership coefficient for cluster A .
Applications
Clustering problems have applications in surface science, biology, medicine, psychology, economics, and many other disciplines.Bioinformatics
In the field of bioinformatics, clustering is used for a number of applications. One use is as apattern recognition
Pattern recognition is the automated recognition of patterns and regularities in data. It has applications in statistical data analysis, signal processing, image analysis, information retrieval, bioinformatics, data compression, computer graphic ...
technique to analyze gene expression data from RNA-sequencing data or other technologies. In this case, genes with similar expression patterns are grouped into the same cluster, and different clusters display distinct, well-separated patterns of expression. Use of clustering can provide insight into gene function and regulation. Because fuzzy clustering allows genes to belong to more than one cluster, it allows for the identification of genes that are conditionally co-regulated or co-expressed. For example, one gene may be acted on by more than one transcription factor
In molecular biology, a transcription factor (TF) (or sequence-specific DNA-binding factor) is a protein that controls the rate of transcription of genetic information from DNA to messenger RNA, by binding to a specific DNA sequence. The fu ...
, and one gene may encode a protein that has more than one function. Thus, fuzzy clustering is more appropriate than hard clustering.
Image analysis
Fuzzy c-means has been a very important tool for image processing in clustering objects in an image. In the 1970s, mathematicians introduced the spatial term into the FCM algorithm to improve the accuracy of clustering under noise.. Furthermore, FCM algorithms have been used to distinguish between different activities using image-based features such as the Hu and the Zernike Moments. Alternatively, Afuzzy logic
Fuzzy logic is a form of many-valued logic in which the truth value of variables may be any real number between 0 and 1. It is employed to handle the concept of partial truth, where the truth value may range between completely true and complet ...
model can be described on fuzzy set
In mathematics, fuzzy sets (a.k.a. uncertain sets) are sets whose elements have degrees of membership. Fuzzy sets were introduced independently by Lotfi A. Zadeh in 1965 as an extension of the classical notion of set.
At the same time, defined ...
s that are defined on three components of the HSL color space HSL and HSV
HSL (for hue, saturation, lightness) and HSV (for hue, saturation, value; also known as HSB, for hue, saturation, brightness) are alternative representations of the RGB color model, designed in the 1970s by computer graphics researchers to more ...
; The membership functions aim to describe colors follow the human intuition of color identification.
Marketing
In marketing, customers can be grouped into fuzzy clusters based on their needs, brand choices, psycho-graphic profiles, or other marketing related partitions.Image processing example

Image segmentation
In digital image processing and computer vision, image segmentation is the process of partitioning a digital image into multiple image segments, also known as image regions or image objects ( sets of pixels). The goal of segmentation is to simpl ...
using k-means clustering
''k''-means clustering is a method of vector quantization, originally from signal processing, that aims to partition ''n'' observations into ''k'' clusters in which each observation belongs to the cluster with the nearest mean (cluster centers o ...
algorithms has long been used for pattern recognition, object detection, and medical imaging. However, due to real world limitations such as noise, shadowing, and variations in cameras, traditional hard clustering is often unable to reliably perform image processing tasks as stated above. Fuzzy clustering has been proposed as a more applicable algorithm in the performance to these tasks. Given is gray scale image that has undergone fuzzy clustering in Matlab. The original image is seen next to a clustered image. Colors are used to give a visual representation of the three distinct clusters used to identify the membership of each pixel. Below, a chart is given that defines the fuzzy membership coefficients of their corresponding intensity values.
Depending on the application for which the fuzzy clustering coefficients are to be used, different pre-processing techniques can be applied to RGB
The RGB color model is an additive color model in which the red, green and blue primary colors of light are added together in various ways to reproduce a broad array of colors. The name of the model comes from the initials of the three additiv ...
images. RGB to HCL HCL may refer to:
Science and medicine
* Hairy cell leukemia, an uncommon and slowly progressing B cell leukemia
* Harvard Cyclotron Laboratory, from 1961 to 2002, a proton accelerator used for research and development
* Hollow-cathode lamp, a s ...
conversion is common practice.
See also
* FLAME Clustering *Cluster Analysis
Cluster analysis or clustering is the task of grouping a set of objects in such a way that objects in the same group (called a cluster) are more similar (in some sense) to each other than to those in other groups (clusters). It is a main task of ...
* Expectation-maximization algorithm (a similar, but more statistically formalized method)
References
{{Reflist Cluster analysis algorithms