Flexural Stress on:
[Wikipedia]
[Google]
[Amazon]
 Flexural strength, also known as modulus of rupture, or bend strength, or transverse rupture strength is a material property, defined as the stress in a material just before it yields in a flexure test. The transverse bending test is most frequently employed, in which a specimen having either a circular or rectangular cross-section is bent until fracture or yielding using a three-point flexural test technique. The flexural strength represents the highest stress experienced within the material at its moment of yield. It is measured in terms of stress, here given the symbol .
Flexural strength, also known as modulus of rupture, or bend strength, or transverse rupture strength is a material property, defined as the stress in a material just before it yields in a flexure test. The transverse bending test is most frequently employed, in which a specimen having either a circular or rectangular cross-section is bent until fracture or yielding using a three-point flexural test technique. The flexural strength represents the highest stress experienced within the material at its moment of yield. It is measured in terms of stress, here given the symbol .
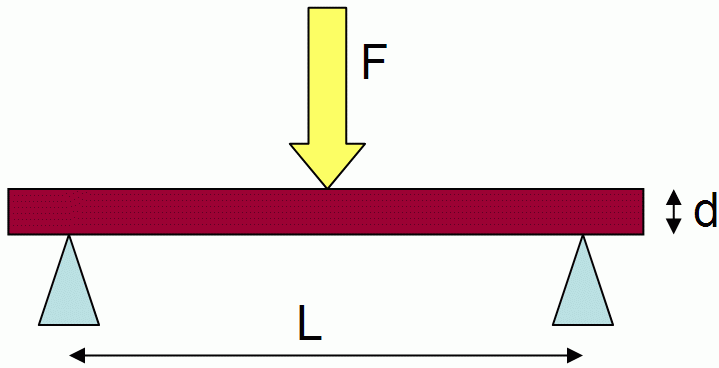 For a rectangular sample under a load in a three-point bending setup (Fig. 3):
:
* ''F'' is the load (force) at the fracture point (N)
* ''L'' is the length of the support span
* ''b'' is width
* ''d'' is thickness
For a rectangular sample under a load in a four-point bending setup where the loading span is one-third of the support span:
:
* ''F'' is the load (force) at the fracture point
* ''L'' is the length of the support (outer) span
* ''b'' is width
* ''d'' is thickness
For the 4 pt bend setup, if the loading span is 1/2 of the support span (i.e. Li = 1/2 L in Fig. 4):
:
If the loading span is neither 1/3 nor 1/2 the support span for the 4 pt bend setup (Fig. 4):
For a rectangular sample under a load in a three-point bending setup (Fig. 3):
:
* ''F'' is the load (force) at the fracture point (N)
* ''L'' is the length of the support span
* ''b'' is width
* ''d'' is thickness
For a rectangular sample under a load in a four-point bending setup where the loading span is one-third of the support span:
:
* ''F'' is the load (force) at the fracture point
* ''L'' is the length of the support (outer) span
* ''b'' is width
* ''d'' is thickness
For the 4 pt bend setup, if the loading span is 1/2 of the support span (i.e. Li = 1/2 L in Fig. 4):
:
If the loading span is neither 1/3 nor 1/2 the support span for the 4 pt bend setup (Fig. 4): :
* ''Li'' is the length of the loading (inner) span
:
* ''Li'' is the length of the loading (inner) span
Introduction
When an object is formed of a single material, like a wooden beam or a steel rod, is bent (Fig. 1), it experiences a range of stresses across its depth (Fig. 2). At the edge of the object on the inside of the bend (concave face) the stress will be at its maximum compressive stress value. At the outside of the bend (convex face) the stress will be at its maximum tensile value. These inner and outer edges of the beam or rod are known as the 'extreme fibers'. Most materials generally fail under tensile stress before they fail under compressive stressFlexural versus tensile strength
The flexural strength would be the same as thetensile strength
Ultimate tensile strength (UTS), often shortened to tensile strength (TS), ultimate strength, or F_\text within equations, is the maximum stress that a material can withstand while being stretched or pulled before breaking. In brittle materials ...
if the material were homogeneous
Homogeneity and heterogeneity are concepts often used in the sciences and statistics relating to the uniformity of a substance or organism. A material or image that is homogeneous is uniform in composition or character (i.e. color, shape, siz ...
. In fact, most materials have small or large defects in them which act to concentrate the stresses locally, effectively causing a localized weakness. When a material is bent only the extreme fibers are at the largest stress so, if those fibers are free from defects, the flexural strength will be controlled by the strength of those intact 'fibers'. However, if the same material was subjected to only tensile forces then all the fibers in the material are at the same stress and failure will initiate when the weakest fiber reaches its limiting tensile stress. Therefore, it is common for flexural strengths to be higher than tensile strengths for the same material. Conversely, a homogeneous material with defects only on its surfaces (e.g., due to scratches) might have a higher tensile strength than flexural strength.
If we don't take into account defects of any kind, it is clear that the material will fail under a bending force which is smaller than the corresponding tensile force. Both of these forces will induce the same failure stress, whose value depends on the strength of the material.
For a rectangular sample, the resulting stress under an axial force is given by the following formula:
:
This stress is not the true stress, since the cross section of the sample is considered to be invariable (engineering stress).
* '''' is the axial load (force) at the fracture point
* '''' is width
* '''' is the depth or thickness of the material
The resulting stress for a rectangular sample under a load in a three-point bending setup (Fig. 3) is given by the formula below (see "Measuring flexural strength").
The equation of these two stresses (failure) yields:
:
Typically, L (length of the support span) is much larger than d, so the fraction is larger than one.
Measuring flexural strength
 For a rectangular sample under a load in a three-point bending setup (Fig. 3):
:
* ''F'' is the load (force) at the fracture point (N)
* ''L'' is the length of the support span
* ''b'' is width
* ''d'' is thickness
For a rectangular sample under a load in a four-point bending setup where the loading span is one-third of the support span:
:
* ''F'' is the load (force) at the fracture point
* ''L'' is the length of the support (outer) span
* ''b'' is width
* ''d'' is thickness
For the 4 pt bend setup, if the loading span is 1/2 of the support span (i.e. Li = 1/2 L in Fig. 4):
:
If the loading span is neither 1/3 nor 1/2 the support span for the 4 pt bend setup (Fig. 4):
For a rectangular sample under a load in a three-point bending setup (Fig. 3):
:
* ''F'' is the load (force) at the fracture point (N)
* ''L'' is the length of the support span
* ''b'' is width
* ''d'' is thickness
For a rectangular sample under a load in a four-point bending setup where the loading span is one-third of the support span:
:
* ''F'' is the load (force) at the fracture point
* ''L'' is the length of the support (outer) span
* ''b'' is width
* ''d'' is thickness
For the 4 pt bend setup, if the loading span is 1/2 of the support span (i.e. Li = 1/2 L in Fig. 4):
:
If the loading span is neither 1/3 nor 1/2 the support span for the 4 pt bend setup (Fig. 4): :
* ''Li'' is the length of the loading (inner) span
:
* ''Li'' is the length of the loading (inner) span
See also
* Euler–Bernoulli beam equation *Flexural modulus In mechanics, the flexural modulus or bending modulus is an intensive property that is computed as the ratio of stress to strain in flexural deformation, or the tendency for a material to resist bending. It is determined from the slope of a stre ...
* Three-point flexural test
* Four-point flexural test
References
* J. M. Hodgkinson (2000), ''Mechanical Testing of Advanced Fibre Composites'', Cambridge: Woodhead Publishing, Ltd., p. 132–133. * William D. Callister, Jr., ''Materials Science and Engineering'', Hoken: John Wiley & Sons, Inc., 2003. * ASTM C1161-02c(2008)e1, Standard Test Method for Flexural Strength of Advanced Ceramics at Ambient Temperature, ASTM International, West Conshohocken, PA. {{Authority control Continuum mechanics