Fibonacci Word Fractal on:
[Wikipedia]
[Google]
[Amazon]
The Fibonacci word fractal is a
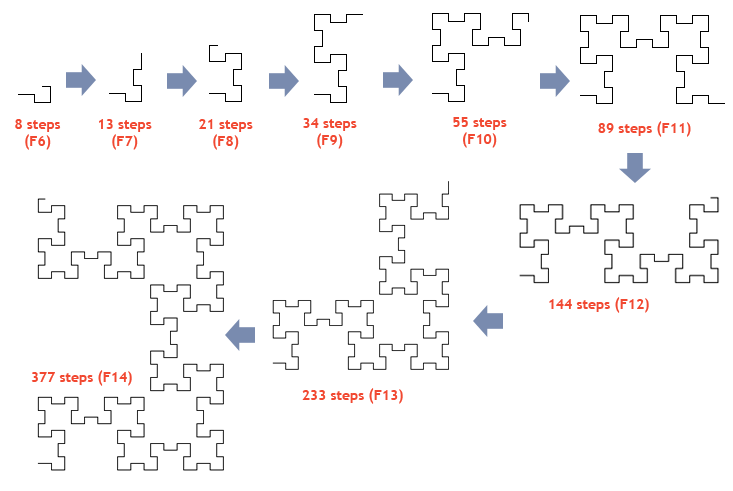
 This curve is built iteratively by applying the Odd–Even Drawing rule to the
This curve is built iteratively by applying the Odd–Even Drawing rule to the
 Some of the Fibonacci word fractal's properties include:
* The curve contains segments, right angles and flat angles.
* The curve never self-intersects and does not contain double points. At the limit, it contains an infinity of points asymptotically close.
* The curve presents self-similarities at all scales. The reduction ratio is . This number, also called the
Some of the Fibonacci word fractal's properties include:
* The curve contains segments, right angles and flat angles.
* The curve never self-intersects and does not contain double points. At the limit, it contains an infinity of points asymptotically close.
* The curve presents self-similarities at all scales. The reduction ratio is . This number, also called the
File:Fibonacci fractal F23 steps.png, Curve after iterations.
File:Fibonacci fractal self-similarities.png, Self-similarities at different scales.
File:FWF Dimensions.png, Dimensions.
File:Fibonacci fractal F21 & F20.png, Construction by juxtaposition (1)
File:Fibonacci Fractal F22 & F21.png, Construction by juxtaposition (2)
File:Fibonacci word fractal, order 18.svg, Order 18, with some sub-rectangles colored.
File:Fibonacci word fractalX.jpg
File:FWF alternative construction.png, Construction by iterated suppression of square patterns.
File:FWF octogons.png, Construction by iterated octagons.
File:Fibonacci word gaskett.png, Construction by iterated collection of 8 square patterns around each square pattern.
File:Fibo 60deg F18.png, With a 60° angle.
File:Inverted Fibonacci fractal.png, Inversion of "0" and "1".
File:Fibonacci word fractal variants.png, Variants generated from the dense Fibonacci word.
File:Fibonacci word fractal compact variant.jpg, The "compact variant"
File:Fibonacci word fractal svastika variant.jpg, The "svastika variant"
File:Fibonacci word fractal diagonal variant.jpg, The "diagonal variant"
File:FWF PI8.png, The "π/8 variant"
File:FWF Samuel Monnier.jpg, Artist creation (Samuel Monnier).
 The juxtaposition of four curves allows the construction of a closed curve enclosing a surface whose
The juxtaposition of four curves allows the construction of a closed curve enclosing a surface whose 
Christoffel and Fibonacci tiles
, ''Lecture Notes in Computer Science: Discrete Geometry for Computer Imagery'', p.67-8. Springer. . * if * otherwise. with and , "turn left" and "turn right", and . Several remarkable properties:A. Blondin-Massé, S. Labbé, S. Brlek, M. Mendès-France (2011).
Fibonacci snowflakes
. * It is the Fibonacci tile associated to the "diagonal variant" previously defined. * It tiles the plane at any order. * It tiles the plane by translation in two different ways. * its
Generate a Fibonacci word fractal
, ''OnlineMathTools.com''. {{Fractals Fractals Fractal curves
fractal curve
A fractal curve is, loosely, a mathematical curve (mathematics), curve whose shape retains the same general pattern of Pathological (mathematics), irregularity, regardless of how high it is magnified, that is, its graph takes the form of a fract ...
defined on the plane from the Fibonacci word
A Fibonacci word is a specific sequence of Binary numeral system, binary digits (or symbols from any two-letter Alphabet (formal languages), alphabet). The Fibonacci word is formed by repeated concatenation in the same way that the Fibonacci num ...
.
Definition

 This curve is built iteratively by applying the Odd–Even Drawing rule to the
This curve is built iteratively by applying the Odd–Even Drawing rule to the Fibonacci word
A Fibonacci word is a specific sequence of Binary numeral system, binary digits (or symbols from any two-letter Alphabet (formal languages), alphabet). The Fibonacci word is formed by repeated concatenation in the same way that the Fibonacci num ...
0100101001001...:
For each digit at position ''k'':
# If the digit is 0:
#* Draw a line segment then turn 90° to the left if ''k'' is even
Even may refer to:
General
* Even (given name), a Norwegian male personal name
* Even (surname), a Breton surname
* Even (people), an ethnic group from Siberia and Russian Far East
**Even language, a language spoken by the Evens
* Odd and Even, a ...
#* Draw a line segment then Turn 90° to the right if ''k'' is odd
# If the digit is 1:
#* Draw a line segment and stay straight
To a Fibonacci word of length (the ''n''th Fibonacci number
In mathematics, the Fibonacci sequence is a Integer sequence, sequence in which each element is the sum of the two elements that precede it. Numbers that are part of the Fibonacci sequence are known as Fibonacci numbers, commonly denoted . Many w ...
) is associated a curve made of segments. The curve displays three different aspects whether ''n'' is in the form 3''k'', 3''k'' + 1, or 3''k'' + 2.
Properties
 Some of the Fibonacci word fractal's properties include:
* The curve contains segments, right angles and flat angles.
* The curve never self-intersects and does not contain double points. At the limit, it contains an infinity of points asymptotically close.
* The curve presents self-similarities at all scales. The reduction ratio is . This number, also called the
Some of the Fibonacci word fractal's properties include:
* The curve contains segments, right angles and flat angles.
* The curve never self-intersects and does not contain double points. At the limit, it contains an infinity of points asymptotically close.
* The curve presents self-similarities at all scales. The reduction ratio is . This number, also called the silver ratio
In mathematics, the silver ratio is a geometrical aspect ratio, proportion with exact value the positive polynomial root, solution of the equation
The name ''silver ratio'' results from analogy with the golden ratio, the positive solution of ...
, is present in a great number of properties listed below.
* The number of self-similarities at level ''n'' is a Fibonacci number
In mathematics, the Fibonacci sequence is a Integer sequence, sequence in which each element is the sum of the two elements that precede it. Numbers that are part of the Fibonacci sequence are known as Fibonacci numbers, commonly denoted . Many w ...
\ −1. (more precisely: ).
* The curve encloses an infinity of square structures of decreasing sizes in a ratio (see figure). The number of those square structures is a Fibonacci number.
* The curve can also be constructed in different ways (see gallery below):
** Iterated function system
In mathematics, iterated function systems (IFSs) are a method of constructing fractals; the resulting fractals are often self-similar. IFS fractals are more related to set theory than fractal geometry. They were introduced in 1981.
IFS fractals ...
of 4 and 1 homothety of ratio and
** By joining together the curves and
** Lindenmayer system
An L-system or Lindenmayer system is a parallel rewriting system and a type of formal grammar. An L-system consists of an alphabet of symbols that can be used to make strings, a collection of production rules that expand each symbol into some ...
** By an iterated construction of 8 square patterns around each square pattern.
** By an iterated construction of octagon
In geometry, an octagon () is an eight-sided polygon or 8-gon.
A '' regular octagon'' has Schläfli symbol and can also be constructed as a quasiregular truncated square, t, which alternates two types of edges. A truncated octagon, t is a ...
s
* The Hausdorff dimension
In mathematics, Hausdorff dimension is a measure of ''roughness'', or more specifically, fractal dimension, that was introduced in 1918 by mathematician Felix Hausdorff. For instance, the Hausdorff dimension of a single point is zero, of a line ...
of the Fibonacci word fractal is , with the golden ratio
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their summation, sum to the larger of the two quantities. Expressed algebraically, for quantities and with , is in a golden ratio to if
\fr ...
.
* Generalizing to an angle between 0 and , its Hausdorff dimension is , with .
* The Hausdorff dimension of its frontier is .
* Exchanging the roles of "0" and "1" in the Fibonacci word, or in the drawing rule yields a similar curve, but oriented 45°.
* From the Fibonacci word, one can define the «dense Fibonacci word», on an alphabet of 3 letters: 102210221102110211022102211021102110221022102211021... . The usage, on this word, of a more simple drawing rule, defines an infinite set of variants of the curve, among which:
** a "diagonal variant"
** a "svastika variant"
** a "compact variant"
* It is conjecture
In mathematics, a conjecture is a conclusion or a proposition that is proffered on a tentative basis without proof. Some conjectures, such as the Riemann hypothesis or Fermat's conjecture (now a theorem, proven in 1995 by Andrew Wiles), ha ...
d that the Fibonacci word fractal appears for every sturmian word
In mathematics, a Sturmian word (Sturmian sequence or billiard sequence), named after Jacques Charles François Sturm, is a certain kind of infinitely long string (computer science), sequence of characters. Such a sequence can be generated by cons ...
for which the slope, written in continued fraction expansion, ends with an infinite sequence of "1"s.
Gallery
The Fibonacci tile
 The juxtaposition of four curves allows the construction of a closed curve enclosing a surface whose
The juxtaposition of four curves allows the construction of a closed curve enclosing a surface whose area
Area is the measure of a region's size on a surface. The area of a plane region or ''plane area'' refers to the area of a shape or planar lamina, while '' surface area'' refers to the area of an open surface or the boundary of a three-di ...
is not null. This curve is called a "Fibonacci tile".
* The Fibonacci tile almost tiles the plane. The juxtaposition of 4 tiles (see illustration) leaves at the center a free square whose area tends to zero as ''k'' tends to infinity. At the limit, the infinite Fibonacci tile tiles the plane.
* If the tile is enclosed in a square of side 1, then its area tends to .

Fibonacci snowflake
The Fibonacci snowflake is a Fibonacci tile defined by:Blondin-Massé, Alexandre; Brlek, Srečko; Garon, Ariane; and Labbé, Sébastien (2009).Christoffel and Fibonacci tiles
, ''Lecture Notes in Computer Science: Discrete Geometry for Computer Imagery'', p.67-8. Springer. . * if * otherwise. with and , "turn left" and "turn right", and . Several remarkable properties:A. Blondin-Massé, S. Labbé, S. Brlek, M. Mendès-France (2011).
Fibonacci snowflakes
. * It is the Fibonacci tile associated to the "diagonal variant" previously defined. * It tiles the plane at any order. * It tiles the plane by translation in two different ways. * its
perimeter
A perimeter is the length of a closed boundary that encompasses, surrounds, or outlines either a two-dimensional shape or a one-dimensional line. The perimeter of a circle or an ellipse is called its circumference.
Calculating the perimet ...
at order ''n'' equals , where is the ''n''th Fibonacci number
In mathematics, the Fibonacci sequence is a Integer sequence, sequence in which each element is the sum of the two elements that precede it. Numbers that are part of the Fibonacci sequence are known as Fibonacci numbers, commonly denoted . Many w ...
.
* its area at order ''n'' follows the successive indexes of odd row of the Pell sequence
In mathematics, the Pell numbers are an infinite sequence of integers, known since ancient times, that comprise the denominators of the closest rational approximations to the square root of 2. This sequence of approximations begins , , , , an ...
(defined by ).
See also
*Golden ratio
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their summation, sum to the larger of the two quantities. Expressed algebraically, for quantities and with , is in a golden ratio to if
\fr ...
* Fibonacci number
In mathematics, the Fibonacci sequence is a Integer sequence, sequence in which each element is the sum of the two elements that precede it. Numbers that are part of the Fibonacci sequence are known as Fibonacci numbers, commonly denoted . Many w ...
* Fibonacci word
A Fibonacci word is a specific sequence of Binary numeral system, binary digits (or symbols from any two-letter Alphabet (formal languages), alphabet). The Fibonacci word is formed by repeated concatenation in the same way that the Fibonacci num ...
* List of fractals by Hausdorff dimension
According to Benoit Mandelbrot, "A fractal is by definition a set for which the Hausdorff-Besicovitch dimension strictly exceeds the topological dimension."
Presented here is a list of fractals, ordered by increasing Hausdorff dimension, to ill ...
References
External links
Generate a Fibonacci word fractal
, ''OnlineMathTools.com''. {{Fractals Fractals Fractal curves