Fermi's golden rule on:
[Wikipedia]
[Google]
[Amazon]
In
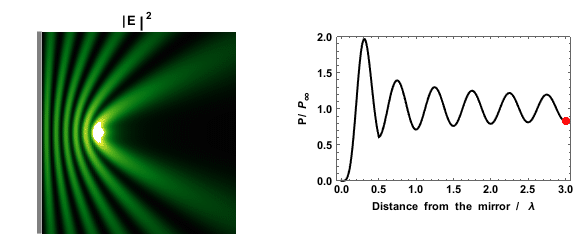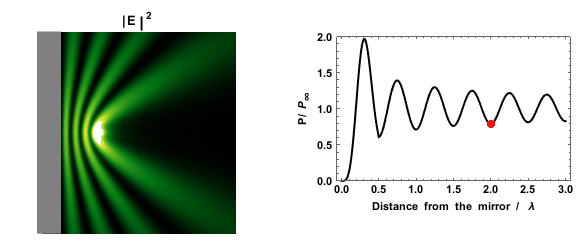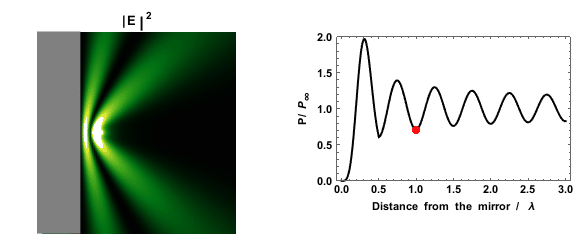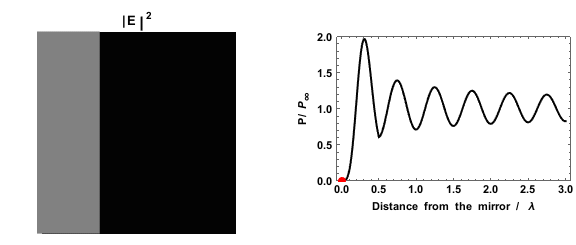 Fermi's golden rule predicts that the probability that an excited state will decay depends on the density of states. This can be seen experimentally by measuring the decay rate of a dipole near a mirror: as the presence of the mirror creates regions of higher and lower density of states, the measured decay rate depends on the distance between the mirror and the dipole.
Fermi's golden rule predicts that the probability that an excited state will decay depends on the density of states. This can be seen experimentally by measuring the decay rate of a dipole near a mirror: as the presence of the mirror creates regions of higher and lower density of states, the measured decay rate depends on the distance between the mirror and the dipole.
More information on Fermi's golden ruleDerivation of Fermi’s Golden RuleTime-dependent perturbation theoryFermi's golden rule: its derivation and breakdown by an ideal model
{{DEFAULTSORT:Fermi's Golden Rule Equations of physics Perturbation theory Mathematical physics
quantum physics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
, Fermi's golden rule is a formula that describes the transition rate (the probability of a transition per unit time) from one energy eigenstate
In quantum physics, a quantum state is a mathematical entity that embodies the knowledge of a quantum system. Quantum mechanics specifies the construction, evolution, and measurement of a quantum state. The result is a prediction for the system re ...
of a quantum system to a group of energy eigenstates in a continuum, as a result of a weak perturbation. This transition rate is effectively independent of time (so long as the strength of the perturbation is independent of time) and is proportional to the strength of the coupling between the initial and final states of the system (described by the square of the matrix element of the perturbation) as well as the density of states
In condensed matter physics, the density of states (DOS) of a system describes the number of allowed modes or quantum state, states per unit energy range. The density of states is defined as where N(E)\delta E is the number of states in the syste ...
. It is also applicable when the final state is discrete, i.e. it is not part of a continuum, if there is some decoherence
Quantum decoherence is the loss of quantum coherence. It involves generally a loss of information of a system to its environment. Quantum decoherence has been studied to understand how quantum systems convert to systems that can be expla ...
in the process, like relaxation or collision of the atoms, or like noise in the perturbation, in which case the density of states is replaced by the reciprocal of the decoherence bandwidth.
Historical background
Although the rule is named afterEnrico Fermi
Enrico Fermi (; 29 September 1901 – 28 November 1954) was an Italian and naturalized American physicist, renowned for being the creator of the world's first artificial nuclear reactor, the Chicago Pile-1, and a member of the Manhattan Project ...
, the first to obtain the formula was Paul Dirac
Paul Adrien Maurice Dirac ( ; 8 August 1902 – 20 October 1984) was an English mathematician and Theoretical physics, theoretical physicist who is considered to be one of the founders of quantum mechanics. Dirac laid the foundations for bot ...
, as he had twenty years earlier formulated a virtually identical equation, including the three components of a constant, the matrix element of the perturbation and an energy difference. It was given this name because, on account of its importance, Fermi called it "golden rule No. 2".
Most uses of the term Fermi's golden rule are referring to "golden rule No. 2", but Fermi's "golden rule No. 1" is of a similar form and considers the probability of indirect transitions per unit time.
The rate and its derivation
Fermi's golden rule describes a system that begins in aneigenstate
In quantum physics, a quantum state is a mathematical entity that embodies the knowledge of a quantum system. Quantum mechanics specifies the construction, evolution, and measurement of a quantum state. The result is a prediction for the system re ...
of an unperturbed Hamiltonian
Hamiltonian may refer to:
* Hamiltonian mechanics, a function that represents the total energy of a system
* Hamiltonian (quantum mechanics), an operator corresponding to the total energy of that system
** Dyall Hamiltonian, a modified Hamiltonian ...
and considers the effect of a perturbing Hamiltonian applied to the system. If is time-independent, the system goes only into those states in the continuum that have the same energy as the initial state. If is oscillating sinusoidally as a function of time (i.e. it is a harmonic perturbation) with an angular frequency
In physics, angular frequency (symbol ''ω''), also called angular speed and angular rate, is a scalar measure of the angle rate (the angle per unit time) or the temporal rate of change of the phase argument of a sinusoidal waveform or sine ...
, the transition is into states with energies that differ by from the energy of the initial state.
In both cases, the ''transition probability per unit of time'' from the initial state to a set of final states is essentially constant. It is given, to first-order approximation, by
where is the matrix element (in bra–ket notation
Bra–ket notation, also called Dirac notation, is a notation for linear algebra and linear operators on complex vector spaces together with their dual space both in the finite-dimensional and infinite-dimensional case. It is specifically de ...
) of the perturbation between the final and initial states, and is the density of states
In condensed matter physics, the density of states (DOS) of a system describes the number of allowed modes or quantum state, states per unit energy range. The density of states is defined as where N(E)\delta E is the number of states in the syste ...
(number of continuum states divided by in the infinitesimally small energy interval to ) at the energy of the final states. This transition probability is also called "decay probability" and is related to the inverse of the mean lifetime
A quantity is subject to exponential decay if it decreases at a rate proportional to its current value. Symbolically, this process can be expressed by the following differential equation, where is the quantity and ( lambda) is a positive ra ...
. Thus, the probability of finding the system in state is proportional to .
The standard way to derive the equation is to start with time-dependent perturbation theory and to take the limit for absorption under the assumption that the time of the measurement is much larger than the time needed for the transition.
Only the magnitude of the matrix element enters the Fermi's golden rule. The phase of this matrix element, however, contains separate information about the transition process.
It appears in expressions that complement the golden rule in the semiclassical Boltzmann equation
The Boltzmann equation or Boltzmann transport equation (BTE) describes the statistical behaviour of a thermodynamic system not in a state of equilibrium; it was devised by Ludwig Boltzmann in 1872.Encyclopaedia of Physics (2nd Edition), R. G ...
approach to electron transport.
While the Golden rule is commonly stated and derived in the terms above, the final state (continuum) wave function is often rather vaguely described, and not normalized correctly (and the normalisation is used in the derivation). The problem is that in order to produce a continuum there can be no spatial confinement (which would necessarily discretise the spectrum), and therefore the continuum wave functions must have infinite extent, and in turn this means that the normalisation is infinite, not unity. If the interactions depend on the energy of the continuum state, but not any other quantum numbers, it is usual to normalise continuum wave-functions with energy labelled , by writing where is the Dirac delta function
In mathematical analysis, the Dirac delta function (or distribution), also known as the unit impulse, is a generalized function on the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line ...
, and effectively a factor of the square-root of the density of states is included into . In this case, the continuum wave function has dimensions of , and the Golden Rule is now
where refers to the continuum state with the same energy as the discrete state . For example, correctly normalized continuum wave functions for the case of a free electron in the vicinity of a hydrogen atom are available in Bethe and Salpeter.
Applications
Semiconductors
The Fermi's golden rule can be used for calculating the transition probability rate for an electron that is excited by a photon from the valence band to the conduction band in a direct band-gap semiconductor, and also for when the electron recombines with the hole and emits a photon. Consider a photon of frequency and wavevector , where the light dispersion relation is and is the index of refraction. Using the Coulomb gauge where and , the vector potential of light is given by where the resulting electric field is For an electron in the valence band, the Hamiltonian is where is the potential of the crystal, and are the charge and mass of an electron, and is the momentum operator. Here we consider process involving one photon and first order in . The resulting Hamiltonian is where is the perturbation of light. From here on we consider vertical optical dipole transition, and thus have transition probability based on time-dependent perturbation theory that with where is the light polarization vector. and are the Bloch wavefunction of the initial and final states. Here the transition probability needs to satisfy the energy conservation given by . From perturbation it is evident that the heart of the calculation lies in the matrix elements shown in the bracket. For the initial and final states in valence and conduction bands, we have and , respectively and if the operator does not act on the spin, the electron stays in the same spin state and hence we can write the Bloch wavefunction of the initial and final states as where is the number of unit cells with volume . Calculating using these wavefunctions, and focusing on emission (photoluminescence
Photoluminescence (abbreviated as PL) is light emission from any form of matter after the absorption of photons (electromagnetic radiation). It is one of many forms of luminescence (light emission) and is initiated by photoexcitation (i.e. phot ...
) rather than absorption, we are led to the transition rate
where defined as the optical transition dipole moment is qualitatively the expectation value and in this situation takes the form
Finally, we want to know the total transition rate . Hence we need to sum over all possible initial and final states that can satisfy the energy conservation (i.e. an integral of the Brillouin zone
In mathematics and solid state physics, the first Brillouin zone (named after Léon Brillouin) is a uniquely defined primitive cell in reciprocal space
Reciprocal lattice is a concept associated with solids with translational symmetry whic ...
in the ''k''-space), and take into account spin degeneracy, which after calculation results in
where is the joint valence-conduction density of states (i.e. the density of pair of states; one occupied valence state, one empty conduction state). In 3D, this is
but the joint DOS is different for 2D, 1D, and 0D.
We note that in a general way we can express the Fermi's golden rule for semiconductors as
In the same manner, the stationary DC photocurrent with amplitude proportional to the square of the field of light is
where is the relaxation time, and are the
difference of the group velocity and Fermi-Dirac distribution between possible the initial and
final states. Here defines the optical transition dipole. Due to the commutation relation between position and the Hamiltonian, we can also rewrite the transition dipole and photocurrent in terms of position operator matrix using . This effect can only exist in systems with broken inversion symmetry and nonzero components of the photocurrent can be obtained by symmetry arguments.
Scanning tunneling microscopy
In ascanning tunneling microscope
A scanning tunneling microscope (STM) is a type of scanning probe microscope used for imaging surfaces at the atomic level. Its development in 1981 earned its inventors, Gerd Binnig and Heinrich Rohrer, then at IBM Zürich, the Nobel Prize in ...
, the Fermi's golden rule is used in deriving the tunneling current. It takes the form
where is the tunneling matrix element.
Quantum optics
When considering energy level transitions between two discrete states, Fermi's golden rule is written as where is the density of photon states at a given energy, is thephoton
A photon () is an elementary particle that is a quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves, and the force carrier for the electromagnetic force. Photons are massless particles that can ...
energy, and is the angular frequency
In physics, angular frequency (symbol ''ω''), also called angular speed and angular rate, is a scalar measure of the angle rate (the angle per unit time) or the temporal rate of change of the phase argument of a sinusoidal waveform or sine ...
. This alternative expression relies on the fact that there is a continuum of final (photon) states, i.e. the range of allowed photon energies is continuous.
Drexhage experiment
 Fermi's golden rule predicts that the probability that an excited state will decay depends on the density of states. This can be seen experimentally by measuring the decay rate of a dipole near a mirror: as the presence of the mirror creates regions of higher and lower density of states, the measured decay rate depends on the distance between the mirror and the dipole.
Fermi's golden rule predicts that the probability that an excited state will decay depends on the density of states. This can be seen experimentally by measuring the decay rate of a dipole near a mirror: as the presence of the mirror creates regions of higher and lower density of states, the measured decay rate depends on the distance between the mirror and the dipole.
See also
* * * * * * Sargent's ruleReferences
External links
More information on Fermi's golden rule
{{DEFAULTSORT:Fermi's Golden Rule Equations of physics Perturbation theory Mathematical physics