FD-DEVS on:
[Wikipedia]
[Google]
[Amazon]
FD-DEVS (Finite & Deterministic Discrete Event System Specification) is a formalism for modeling and analyzing discrete event dynamic systems in both simulation and verification ways. FD-DEVS also provides modular and hierarchical modeling features which have been inherited from Classic DEVS.
 Consider a single ping-pong match in which there are two players. Each player can be modeled by FD-DEVS such that the player model has an input event ''?receive'' and an output event ''!send'', and it has two states: ''Send'' and ''Wait''. Once the player gets into "Send", it will generates "!send" and go back to "Wait" after the sending time which is 0.1 time unit. When staying at "Wait" and if it gets "?receive", it changes into "Send" again. In other words, the player model stays at "Wait" forever unless it gets "?receive".
To make a complete ping-pong match, one player starts as an offender whose initial state is "Send" and the other starts as a defender whose initial state is "Wait". Thus in Fig. 1. Player A is the initial offender and Player B is the initial defender. In addition, to make the game continue, each player's "?send" event should be coupled to the other player's "?receive" as shown in Fig. 1.
Consider a single ping-pong match in which there are two players. Each player can be modeled by FD-DEVS such that the player model has an input event ''?receive'' and an output event ''!send'', and it has two states: ''Send'' and ''Wait''. Once the player gets into "Send", it will generates "!send" and go back to "Wait" after the sending time which is 0.1 time unit. When staying at "Wait" and if it gets "?receive", it changes into "Send" again. In other words, the player model stays at "Wait" forever unless it gets "?receive".
To make a complete ping-pong match, one player starts as an offender whose initial state is "Send" and the other starts as a defender whose initial state is "Wait". Thus in Fig. 1. Player A is the initial offender and Player B is the initial defender. In addition, to make the game continue, each player's "?send" event should be coupled to the other player's "?receive" as shown in Fig. 1.
 Consider a toaster in which there are two slots that have their own start knobs as shown in Fig. 2(a). Each slot has the identical functionality except their toasting time. Initially, the knob is not pushed, but if one pushes the knob, the associated slot starts toasting for its toasting time: 20 seconds for the left slot, 40 seconds for the right slot. After the toasting time, each slot and its knobs pop up. Notice that even though one tries to push a knob when its associated slot is toasting, nothing happens.
One can model it with FD-DEVS as shown in Fig. 2(b). Two slots are modeled as atomic FD-DEVS whose input event is "?push" and output event is "!pop", states are "Idle" (I) and "Toast" (T) with the initial state is "idle". When it is "Idle" and receives "?push" (because one pushes the knob), its state changes to "Toast". In other words, it stays at "Idle" forever unless it receives "?push" event. 20 (res. 40) seconds later the left (res. right) slot returns to "Idle".
Consider a toaster in which there are two slots that have their own start knobs as shown in Fig. 2(a). Each slot has the identical functionality except their toasting time. Initially, the knob is not pushed, but if one pushes the knob, the associated slot starts toasting for its toasting time: 20 seconds for the left slot, 40 seconds for the right slot. After the toasting time, each slot and its knobs pop up. Notice that even though one tries to push a knob when its associated slot is toasting, nothing happens.
One can model it with FD-DEVS as shown in Fig. 2(b). Two slots are modeled as atomic FD-DEVS whose input event is "?push" and output event is "!pop", states are "Idle" (I) and "Toast" (T) with the initial state is "idle". When it is "Idle" and receives "?push" (because one pushes the knob), its state changes to "Toast". In other words, it stays at "Idle" forever unless it receives "?push" event. 20 (res. 40) seconds later the left (res. right) slot returns to "Idle".
 ; FD-DEVS is a sub-class of DEVS
A FD-DEVS model, is DEVS where
* of are the same as those of .
*
*
* Given a state ,
* Given a state and an input event ,
* Given a state , if
* Given a state , if
For details of DEVS behavior, the readers can refer to Behavior of Atomic DEVS
;Behavior of Ping-Pong Player A
Fig. 3. shows an event segment (top) and the associated state trajectory (bottom) of Player A who plays the ping-pong game introduced in Fig. 1. In Fig. 3. the status of Player A is described as (state, lifespan, elapsed time)=() and the line segment of the bottom of Fig. 3. denotes the value of the elapsed time. Since the initial state of Player A is "Send" and its lifetime is 0.1 seconds, the height of (Send, 0.1, ) is 0.1 which is the value of . After changing into (Wait, inf,inf in Fig 3. means . 0) when is reset by 0, Player A doesn't know when becomes 0 again. However, since Player B sends back the ball to Player A 0.1 second later, Player A gets back to (Send, 0.1 0) at time 0.2. From that time, 0.1 seconds later when Player A's status becomes (Send, 0.1, 0.1), Player A sends back the ball to Player B and gets into (Wait, inf, 0). Thus, this cyclic state transitions which move "Send" to "Wait" back and forth will go forever.
; FD-DEVS is a sub-class of DEVS
A FD-DEVS model, is DEVS where
* of are the same as those of .
*
*
* Given a state ,
* Given a state and an input event ,
* Given a state , if
* Given a state , if
For details of DEVS behavior, the readers can refer to Behavior of Atomic DEVS
;Behavior of Ping-Pong Player A
Fig. 3. shows an event segment (top) and the associated state trajectory (bottom) of Player A who plays the ping-pong game introduced in Fig. 1. In Fig. 3. the status of Player A is described as (state, lifespan, elapsed time)=() and the line segment of the bottom of Fig. 3. denotes the value of the elapsed time. Since the initial state of Player A is "Send" and its lifetime is 0.1 seconds, the height of (Send, 0.1, ) is 0.1 which is the value of . After changing into (Wait, inf,inf in Fig 3. means . 0) when is reset by 0, Player A doesn't know when becomes 0 again. However, since Player B sends back the ball to Player A 0.1 second later, Player A gets back to (Send, 0.1 0) at time 0.2. From that time, 0.1 seconds later when Player A's status becomes (Send, 0.1, 0.1), Player A sends back the ball to Player B and gets into (Wait, inf, 0). Thus, this cyclic state transitions which move "Send" to "Wait" back and forth will go forever.
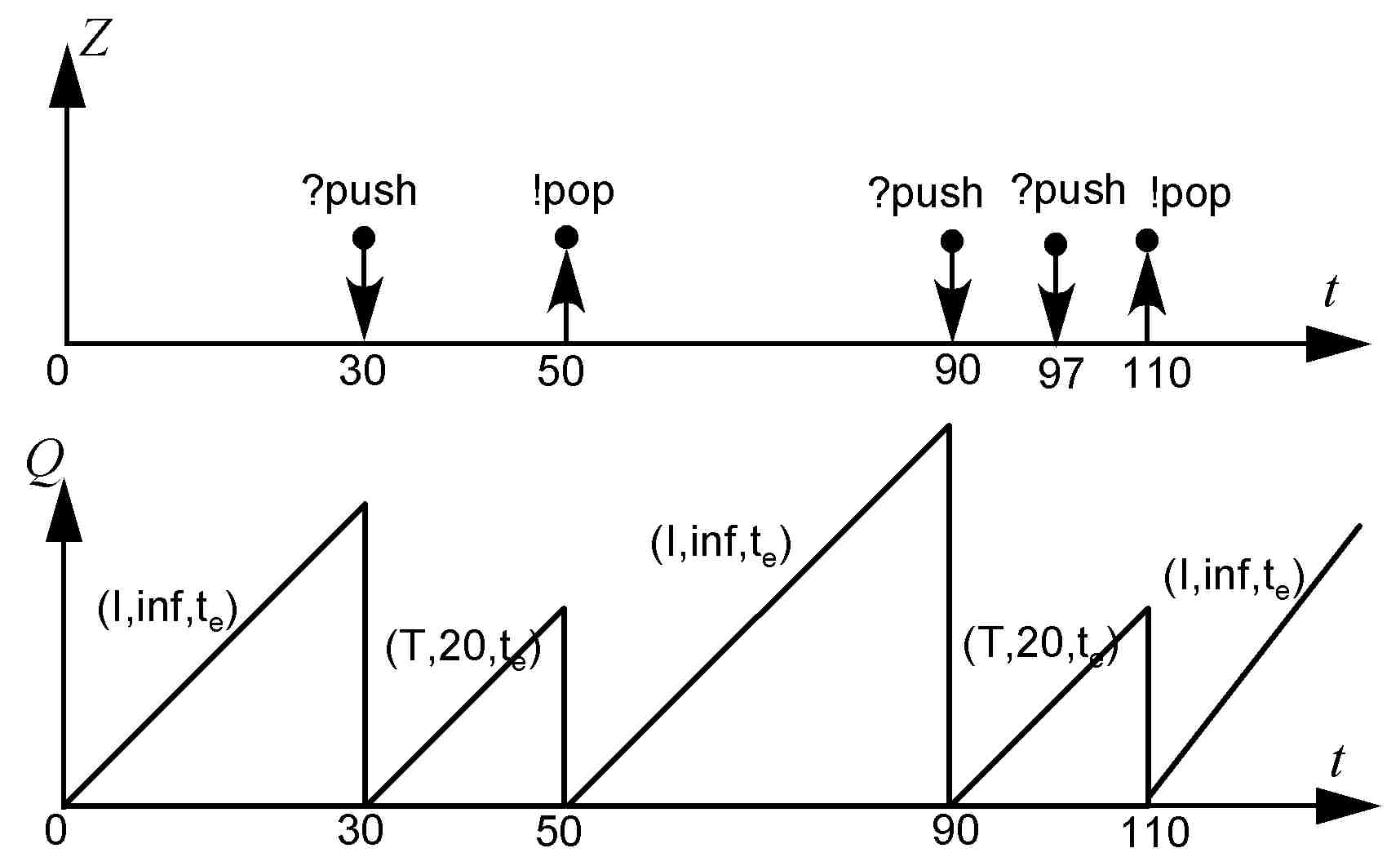 ;Behavior of a Toaster
Fig. 4. shows an event segment (top) and the associated state trajectory (bottom) of the left slot of the two-slot toaster introduced in Fig. 2. Like Fig.3, the status of the left slot is described as (state, lifespan, elapsed time)=() in Fig. 4. Since the initial state of the toaster is "I" and its lifetime is infinity, the height of (Wait, inf, ) can be determined by when ?push occurs. Fig. 4. illustrates the case ?push happens at time 40 and the toaster changes into (T, 20, 0). From that time, 20 seconds later when its status becomes (T, 20, 20), the toaster gets back to (Wait, inf, 0) where we don't know when it gets back to "Toast" again. Fig. 4. shows the case that ?push occurs at time 90 so the toaster get into (T,20,0). Notice that even though there someone push again at time 97, that status (T, 20, 7) doesn't change at all because (T,?push)=(T,1).
;Behavior of a Toaster
Fig. 4. shows an event segment (top) and the associated state trajectory (bottom) of the left slot of the two-slot toaster introduced in Fig. 2. Like Fig.3, the status of the left slot is described as (state, lifespan, elapsed time)=() in Fig. 4. Since the initial state of the toaster is "I" and its lifetime is infinity, the height of (Wait, inf, ) can be determined by when ?push occurs. Fig. 4. illustrates the case ?push happens at time 40 and the toaster changes into (T, 20, 0). From that time, 20 seconds later when its status becomes (T, 20, 20), the toaster gets back to (Wait, inf, 0) where we don't know when it gets back to "Toast" again. Fig. 4. shows the case that ?push occurs at time 90 so the toaster get into (T,20,0). Notice that even though there someone push again at time 97, that status (T, 20, 7) doesn't change at all because (T,?push)=(T,1).

* Z06aM. H. Hwang and Bernard Zeigler, "A Modular Verification Framework using Finite and Deterministic DEVS", ''Proceedings of 2006 DEVS Symposium'', pp57–65, Huntsville, Alabama, USA, (Available at http://www.acims.arizona.edu ) * Z06bM. H. Hwang and Bernard Zeigler, "A Reachable Graph of Finite and Deterministic DEVS Networks", ''Proceedings of 2006 DEVS Symposium'', pp48–56, Huntsville, Alabama, USA, (Available at http://www.acims.arizona.edu ) * Z07M.H. Hwang and Bernard Zeigler, "Reachability Graph of Finite & Deterministic DEVS", IEEE Transactions on Automation Science and Engineering, Volume 6, Issue 3, 2009, pp. 454–467, https://ieeexplore.ieee.org/document/5071137/;jsessionid=6E63EA120D0510F93D51D6C18728D31C?isnumber=5153598&arnumber=5071137&count=19&index=7 * CMZ09José L. Risco-Martín, Jesús M. de la Cruz, Saurabh Mittal and Bernard Zeigler, "eUDEVS: Executable UML with DEVS Theory of Modeling and Simulation", SIMULATION, Transaction of The Society for Modeling and Simulation International, Volume 85, No. 11-12, 2009, pp. 750–777, http://sim.sagepub.com/content/85/11-12/750.short *
History
FD-DEVS was originally named as "Schedule-Controllable DEVS" wang05and designed to support verification analysis of its networks which had been an open problem of DEVS formalism for 30 years. In addition, it was also designated to resolve the so-called " OPNA" problem ofSP-DEVS SP-DEVS abbreviating "Schedule-Preserving Discrete Event System Specification" is a formalism for modeling and analyzing discrete event systems in both simulation and verification ways. SP-DEVS also provides modular and hierarchical modeling feature ...
. From the viewpoint of Classic DEVS, FD-DEVS has three restrictions
# finiteness of event sets and state set,
# the lifespan of a state can be scheduled by a rational number or infinity, and
# the internal schedule can be either preserved or updated by an input event.
The third restriction can be also seen as a relaxation from SP-DEVS SP-DEVS abbreviating "Schedule-Preserving Discrete Event System Specification" is a formalism for modeling and analyzing discrete event systems in both simulation and verification ways. SP-DEVS also provides modular and hierarchical modeling feature ...
where the schedule is always preserved by any input events. Due to this relaxation there is no longer OPNA problem, but there is also one limitation that a time-line abstraction which can be used for abstracting elapsed times of SP-DEVS networks is no longer useful for FD-DEVS network wang05 But another time abstraction method ill89which was invented by Prof. D. Dill can be applicable to obtain a finite-vertex reachability graph for FD-DEVS networks.
Examples
Ping-pong game
Two-slot toaster
Atomic FD-DEVS
Formal Definition
where* is ''a finite set of input events''; * is ''a finite set of output events''; * is ''a finite set of states''; * is ''the initial state''; * is ''the time advance function'' which defines the lifespan of a state where is the set of non-negative rational numbers plus infinity. * is ''the external transition function'' which defines how an input event changes the schedule as well as a state of the system. The internal schedule of a state is updated by if , otherwise(i.e., ), the schedule is preserved. * is ''the output and internal transition function'' where and denotes ''the silent event''. The output and internal transition function defines how a state generates an output event, at the same time, how the state changes internally.;Formal Representation of Ping-Pong Player The formal representation of the player in the ping-pong example shown in Fig. 1 can be given as follows. where =; =; =; =Send for Player A, Wait for Player B; (Send)=0.1,(Wait)=; (Wait,?receive)=(Send,1), (Send,?receive)=(Send,0); (Send)=(!send, Wait), (Wait)=(, Wait). ;Formal Representation of One Slot Toaster The formal representation of the slot of Two-slot Toaster Fig. 2(a) and (b) can be given as follows. where =; =; =; =I; (T)=20 for the left slot, 40 for the right slot, (I)=; (I, ?push)=(T,1), (T,?push)=(T,0); (T)=(!pop, I), (I)=(, I). ;Formal Representation of Crosswalk Light Controller As mentioned above, FD-DEVS is an relaxation of SP-DEVS. That means, FD-DEVS is a supper class of SP-DEVS. We would give a model of FD-DEVS of a crosswalk light controller which is used for
SP-DEVS SP-DEVS abbreviating "Schedule-Preserving Discrete Event System Specification" is a formalism for modeling and analyzing discrete event systems in both simulation and verification ways. SP-DEVS also provides modular and hierarchical modeling feature ...
in this Wikipedia. where =; =; =; =BG, (BG)=0.5,(BW)=0.5, (G)=30, (GR)=30,(R)=2, (W)=26, (D)=2; (G,?p)=(GR,0), (s,?p)=(s,0) if s G; (BG)=(!g:1, BW), (BW)=(!w:0, G),(G)=(, G), (GR)=(!g:0, R), (R)=(!w:1, W), (W)=(!w:0, D), (D)=(!g:1, G);
Behaviors of FD-DEVS Models
Advantages
Applicability of Time-Zone Abstraction
The property of non-negative rational-valued lifespans which can be preserved or changed by input events along with finite numbers of states and events guarantees that the behavior of FD-DEVS networks can be abstracted as an equivalent finite-vertex reachability graph by abstracting the infinitely-many values of the elapsed times using the time abstracting technique introduced by Prof. D. Dill ill89 An algorithm generating a finite-vertex reachability graph (RG)has been introduced in Z06a Z07Reachability Graph
Fig. 5. shows the reachability graph of two-slot toaster which was shown in Fig. 2. In the reachability graph, each vertex has its own discrete state and time zone which are ranges of and . For example, for node (6) of Fig. 5, discrete state information is ((E,),(T,40)), and time zone is . Each directed arch shows how its source vertex changes into the destination vertex along with an associated event and a set of reset models. For example, the transition arc (6) to (5) is triggered by ''push1'' event. At that time, the set of the arc denotes that elapsed time of 1 (that is is reset by 0 when transition (6) to (5) occurs. For more detailed information, the reader can refer to Z07Decidability of Safety
As a qualitative property, safety of a FD-DEVS network is decidable by (1) generating RG of the given network and (2) checking whether some bad states are reachable or not Z06bDecidability of Liveness
As a qualitative property, liveness of a FD-DEVS network is decidable by (1) generating RG of the given network, (2) from RG, generating kernel directed acyclic graph (KDAG) in which a vertex isstrongly connected component
In the mathematical theory of directed graphs, a graph is said to be strongly connected if every vertex is reachable from every other vertex. The strongly connected components of an arbitrary directed graph form a partition into subgraphs that a ...
, and (3) checking if a vertex of KDAG contains a state transition cycle which contains a set of liveness states Z06b
Disadvantages
Weak Expressiveness for describing nondeterminism
The features that all characteristic functions, of FD-DEVS are deterministic can be seen as somehow a limitation to model the system that has non-deterministic behaviors. For example, if a player of the ping-pong game shown in Fig. 1. has a stochastic lifespan at "Send" state, FD-DEVS doesn't capture the non-determinism effectively.Tool
For Verification
There are two open source libraries DEVS# written in C# at http://xsy-csharp.sourceforge.net/DEVSsharp/ and XSY written in Python at https://code.google.com/p/x-s-y/ that support some reachability graph-based verification algorithms for finding safeness and liveness.For Simulation via XML
For standardization of DEVS, especially using FDDEVS, Dr. Saurabh Mittal together with co-workers has worked on defining of XML format of FDDEVS. We can find an article at http://www.duniptechnologies.com/research/xfddevs/. This standard XML format was used for UML execution CMZ09.Footnotes
References
* ill89D.L. Dill, "Timing Assumptions and Verification of Finite-State Concurrent Systems", In ''Proceedings of the Workshop on Computer Aided Verification Methods for Finite State Systems'', pp 197–212, Grenoble, France, 1989 * wang05M.H. Hwang, "Generating Finite-State Global Behavior of Reconfigurable Automation Systems: DEVS Approach", ''Proceedings of 2005 IEEE-CASE'', Edmonton, Canada, Aug. 1-2, 2005(Available a* Z06aM. H. Hwang and Bernard Zeigler, "A Modular Verification Framework using Finite and Deterministic DEVS", ''Proceedings of 2006 DEVS Symposium'', pp57–65, Huntsville, Alabama, USA, (Available at http://www.acims.arizona.edu ) * Z06bM. H. Hwang and Bernard Zeigler, "A Reachable Graph of Finite and Deterministic DEVS Networks", ''Proceedings of 2006 DEVS Symposium'', pp48–56, Huntsville, Alabama, USA, (Available at http://www.acims.arizona.edu ) * Z07M.H. Hwang and Bernard Zeigler, "Reachability Graph of Finite & Deterministic DEVS", IEEE Transactions on Automation Science and Engineering, Volume 6, Issue 3, 2009, pp. 454–467, https://ieeexplore.ieee.org/document/5071137/;jsessionid=6E63EA120D0510F93D51D6C18728D31C?isnumber=5153598&arnumber=5071137&count=19&index=7 * CMZ09José L. Risco-Martín, Jesús M. de la Cruz, Saurabh Mittal and Bernard Zeigler, "eUDEVS: Executable UML with DEVS Theory of Modeling and Simulation", SIMULATION, Transaction of The Society for Modeling and Simulation International, Volume 85, No. 11-12, 2009, pp. 750–777, http://sim.sagepub.com/content/85/11-12/750.short *
KP00
KP may refer to:
Businesses and organizations
* ''Komsomolskaya Pravda'', a daily Russian newspaper
* ''KP'' (newspaper), a Ukrainian newspaper
* KP Snacks, a United Kingdom food manufacturer
* Kaiser Permanente, a U.S. health maintenance organi ...
{{DEFAULTSORT:Finite and Deterministic Discrete Event System Specification
Automata (computation)