Enough Injectives on:
[Wikipedia]
[Google]
[Amazon]
In mathematics, especially in the field of category theory, the concept of injective object is a generalization of the concept of
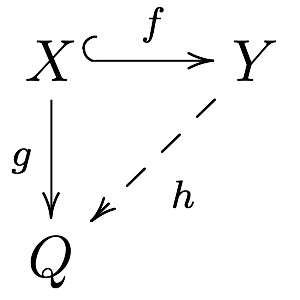 An
An
 Let be a category and let be a class of morphisms of .
An object of is said to be ''''-injective if for every morphism and every morphism in there exists a morphism with .
If is the class of
Let be a category and let be a class of morphisms of .
An object of is said to be ''''-injective if for every morphism and every morphism in there exists a morphism with .
If is the class of
Republished in Reprints and Applications of Categories, No. 17 (2006) pp. 1-507
Wiley (1990). *J. Rosicky, Injectivity and accessible categories *F. Cagliari and S. Montovani, T0-reflection and injective hulls of fibre spaces Category theory de:Injektiver Modul#Injektive Moduln
injective module
In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module ''Q'' that shares certain desirable properties with the Z-module Q of all rational numbers. Specifically, if ''Q'' is a submodule o ...
. This concept is important in cohomology
In mathematics, specifically in homology theory and algebraic topology, cohomology is a general term for a sequence of abelian groups, usually one associated with a topological space, often defined from a cochain complex. Cohomology can be viewe ...
, in homotopy theory and in the theory of model categories. The dual notion is that of a projective object In category theory, the notion of a projective object generalizes the notion of a projective module. Projective objects in abelian categories are used in homological algebra. The dual notion of a projective object is that of an injective object.
...
.
Definition
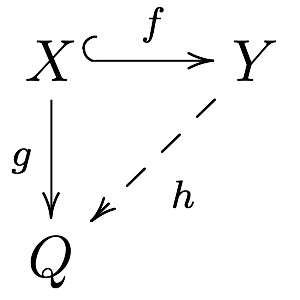 An
An object
Object may refer to:
General meanings
* Object (philosophy), a thing, being, or concept
** Object (abstract), an object which does not exist at any particular time or place
** Physical object, an identifiable collection of matter
* Goal, an ...
in a category
Category, plural categories, may refer to:
Philosophy and general uses
*Categorization, categories in cognitive science, information science and generally
* Category of being
* ''Categories'' (Aristotle)
* Category (Kant)
* Categories (Peirce) ...
is said to be injective if for every monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from to is often denoted with the notation X\hookrightarrow Y.
In the more general setting of category theory, a monomorphism ...
and every morphism there exists a morphism extending to , i.e. such that .
That is, every morphism factors through every monomorphism .
The morphism in the above definition is not required to be uniquely determined by and .
In a locally small
In mathematics, a category (sometimes called an abstract category to distinguish it from a concrete category) is a collection of "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows asso ...
category, it is equivalent to require that the hom functor
In mathematics, specifically in category theory, hom-sets (i.e. sets of morphisms between objects) give rise to important functors to the category of sets. These functors are called hom-functors and have numerous applications in category theory and ...
carries monomorphisms in to surjective set maps.
In Abelian categories
The notion of injectivity was first formulated forabelian categories
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototypical example of an abelian category is the category of ...
, and this is still one of its primary areas of application. When is an abelian category, an object ''Q'' of is injective if and only if
In logic and related fields such as mathematics and philosophy, "if and only if" (shortened as "iff") is a biconditional logical connective between statements, where either both statements are true or both are false.
The connective is b ...
its hom functor
In mathematics, specifically in category theory, hom-sets (i.e. sets of morphisms between objects) give rise to important functors to the category of sets. These functors are called hom-functors and have numerous applications in category theory and ...
HomC(–,''Q'') is exact.
If is an exact sequence
An exact sequence is a sequence of morphisms between objects (for example, groups, rings, modules, and, more generally, objects of an abelian category) such that the image of one morphism equals the kernel of the next.
Definition
In the context ...
in such that ''Q'' is injective, then the sequence splits.
Enough injectives and injective hulls
The category is said to ''have enough injectives'' if for every object ''X'' of , there exists a monomorphism from ''X'' to an injective object. A monomorphism ''g'' in is called anessential monomorphism
In mathematics, specifically category theory, an essential monomorphism is a monomorphism ''f'' in a category ''C'' such that for a morphism ''g'' in ''C'', the morphism g \circ f is a monomorphism only when ''g'' is a monomorphism. Essential mon ...
if for any morphism ''f'', the composite ''fg'' is a monomorphism only if ''f'' is a monomorphism.
If ''g'' is an essential monomorphism with domain ''X'' and an injective codomain ''G'', then ''G'' is called an injective hull of ''X''. The injective hull is then uniquely determined by ''X'' up to a non-canonical isomorphism.
Examples
*In the category ofabelian group
In mathematics, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on the order in which they are written. That is, the group operation is comm ...
s and group homomorphism
In mathematics, given two groups, (''G'', ∗) and (''H'', ·), a group homomorphism from (''G'', ∗) to (''H'', ·) is a function ''h'' : ''G'' → ''H'' such that for all ''u'' and ''v'' in ''G'' it holds that
: h(u*v) = h(u) \cdot h(v)
w ...
s, Ab, an injective object is necessarily a divisible group In mathematics, especially in the field of group theory, a divisible group is an abelian group in which every element can, in some sense, be divided by positive integers, or more accurately, every element is an ''n''th multiple for each positive in ...
. Assuming the axiom of choice, the notions are equivalent.
*In the category of (left) modules
Broadly speaking, modularity is the degree to which a system's components may be separated and recombined, often with the benefit of flexibility and variety in use. The concept of modularity is used primarily to reduce complexity by breaking a s ...
and module homomorphism In algebra, a module homomorphism is a function between modules that preserves the module structures. Explicitly, if ''M'' and ''N'' are left modules over a ring ''R'', then a function f: M \to N is called an ''R''-''module homomorphism'' or an '' ...
s, ''R''-Mod, an injective object is an injective module
In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module ''Q'' that shares certain desirable properties with the Z-module Q of all rational numbers. Specifically, if ''Q'' is a submodule o ...
. ''R''-Mod has injective hull
In mathematics, particularly in algebra, the injective hull (or injective envelope) of a module is both the smallest injective module containing it and the largest essential extension of it. Injective hulls were first described in .
Definition
...
s (as a consequence, ''R''-Mod has enough injectives).
*In the category of metric spaces In category theory, Met is a category that has metric spaces as its objects and metric maps (continuous functions between metric spaces that do not increase any pairwise distance) as its morphisms. This is a category because the composition of two ...
, Met, an injective object is an injective metric space In metric geometry, an injective metric space, or equivalently a hyperconvex metric space, is a metric space with certain properties generalizing those of the real line and of L∞ distances in higher-dimensional vector spaces. These properties ca ...
, and the injective hull of a metric space is its tight span
In metric geometry, the metric envelope or tight span of a metric space ''M'' is an injective metric space into which ''M'' can be embedded. In some sense it consists of all points "between" the points of ''M'', analogous to the convex hull of a ...
.
*In the category of T0 spaces and continuous mapping
In mathematics, a continuous function is a function such that a continuous variation (that is a change without jump) of the argument induces a continuous variation of the value of the function. This means that there are no abrupt changes in valu ...
s, an injective object is always a Scott topology
Scott may refer to:
Places Canada
* Scott, Quebec, municipality in the Nouvelle-Beauce regional municipality in Quebec
* Scott, Saskatchewan, a town in the Rural Municipality of Tramping Lake No. 380
* Rural Municipality of Scott No. 98, Saskat ...
on a continuous lattice
In order theory, a continuous poset is a partially ordered set in which every element is the directed supremum of elements approximating it.
Definitions
Let a,b\in P be two elements of a preordered set (P,\lesssim). Then we say that a approxima ...
, and therefore it is always sober and locally compact.
Uses
If an abelian category has enough injectives, we can form injective resolutions, i.e. for a given object ''X'' we can form a long exact sequence : and one can then define thederived functor
In mathematics, certain functors may be ''derived'' to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.
Motivation
It was noted in vari ...
s of a given functor ''F'' by applying ''F'' to this sequence and computing the homology of the resulting (not necessarily exact) sequence. This approach is used to define Ext, and Tor functors and also the various cohomology
In mathematics, specifically in homology theory and algebraic topology, cohomology is a general term for a sequence of abelian groups, usually one associated with a topological space, often defined from a cochain complex. Cohomology can be viewe ...
theories in group theory
In abstract algebra, group theory studies the algebraic structures known as group (mathematics), groups.
The concept of a group is central to abstract algebra: other well-known algebraic structures, such as ring (mathematics), rings, field ...
, algebraic topology
Algebraic topology is a branch of mathematics that uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify ...
and algebraic geometry. The categories being used are typically functor categories or categories of sheaves of ''O''''X'' modules over some ringed space
In mathematics, a ringed space is a family of (commutative) rings parametrized by open subsets of a topological space together with ring homomorphisms that play roles of restrictions. Precisely, it is a topological space equipped with a sheaf of ...
(''X'', ''O''''X'') or, more generally, any Grothendieck category In mathematics, a Grothendieck category is a certain kind of abelian category, introduced in Alexander Grothendieck's Tôhoku paper of 1957English translation in order to develop the machinery of homological algebra for modules and for sheaves ...
.
Generalization
monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from to is often denoted with the notation X\hookrightarrow Y.
In the more general setting of category theory, a monomorphism ...
s, we are back to the injective objects that were treated above.
The category is said to ''have enough -injectives'' if for every object ''X'' of , there exists an ''''-morphism from ''X'' to an ''''-injective object.
A ''''-morphism ''g'' in is called ''''-essential if for any morphism ''f'', the composite ''fg'' is in '''' only if ''f'' is in ''''.
If ''g'' is a ''''-essential morphism with domain ''X'' and an ''''-injective codomain ''G'', then ''G'' is called an -injective hull of ''X''.
Examples of -injective objects
*In the category ofsimplicial set
In mathematics, a simplicial set is an object composed of ''simplices'' in a specific way. Simplicial sets are higher-dimensional generalizations of directed graphs, partially ordered sets and categories. Formally, a simplicial set may be defined ...
s, the injective objects with respect to the class '''' of anodyne extensions are Kan complex
In mathematics, Kan complexes and Kan fibrations are part of the theory of simplicial set
In mathematics, a simplicial set is an object composed of ''simplices'' in a specific way. Simplicial sets are higher-dimensional generalizations of directed ...
es.
*In the category of partially ordered set
In mathematics, especially order theory, a partially ordered set (also poset) formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a bina ...
s and monotone maps, the complete lattices form the injective objects for the class '''' of order-embedding In order theory, a branch of mathematics, an order embedding is a special kind of monotone function, which provides a way to include one partially ordered set into another. Like Galois connections, order embeddings constitute a notion which is stric ...
s, and the Dedekind–MacNeille completion
In mathematics, specifically order theory, the Dedekind–MacNeille completion of a partially ordered set is the smallest complete lattice that contains it. It is named after Holbrook Mann MacNeille whose 1937 paper first defined and constructed ...
of a partially ordered set is its ''''-injective hull.
See also
*Projective object In category theory, the notion of a projective object generalizes the notion of a projective module. Projective objects in abelian categories are used in homological algebra. The dual notion of a projective object is that of an injective object.
...
Notes
{{reflistReferences
*Jiri Adamek, Horst Herrlich, George Strecker. Abstract and concrete categories: The joy of cats, Chapter 9, Injective Objects and Essential EmbeddingsRepublished in Reprints and Applications of Categories, No. 17 (2006) pp. 1-507
Wiley (1990). *J. Rosicky, Injectivity and accessible categories *F. Cagliari and S. Montovani, T0-reflection and injective hulls of fibre spaces Category theory de:Injektiver Modul#Injektive Moduln