Extension (algebra) on:
[Wikipedia]
[Google]
[Amazon]
In
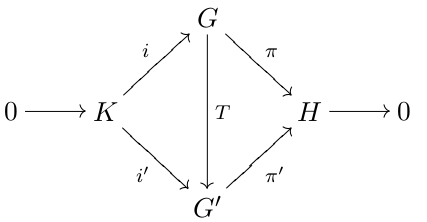 It is important to know when two extensions are equivalent or congruent. We say that the extensions
:
and
:
are equivalent (or congruent) if there exists a group isomorphism making commutative the diagram of Figure 1.
In fact it is sufficient to have a group homomorphism; due to the assumed commutativity of the diagram, the map is forced to be an isomorphism by the
It is important to know when two extensions are equivalent or congruent. We say that the extensions
:
and
:
are equivalent (or congruent) if there exists a group isomorphism making commutative the diagram of Figure 1.
In fact it is sufficient to have a group homomorphism; due to the assumed commutativity of the diagram, the map is forced to be an isomorphism by the
Group Extensions and ''H''3
. From his collection of short mathematical notes.
mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
, a group extension is a general means of describing a group in terms of a particular normal subgroup
In abstract algebra, a normal subgroup (also known as an invariant subgroup or self-conjugate subgroup) is a subgroup that is invariant under conjugation by members of the group of which it is a part. In other words, a subgroup N of the group G i ...
and quotient group
A quotient group or factor group is a mathematical group obtained by aggregating similar elements of a larger group using an equivalence relation that preserves some of the group structure (the rest of the structure is "factored" out). For examp ...
. If and are two groups, then is an extension of by if there is a short exact sequence
:
If is an extension of by , then is a group, is a normal subgroup
In abstract algebra, a normal subgroup (also known as an invariant subgroup or self-conjugate subgroup) is a subgroup that is invariant under conjugation by members of the group of which it is a part. In other words, a subgroup N of the group G i ...
of and the quotient group
A quotient group or factor group is a mathematical group obtained by aggregating similar elements of a larger group using an equivalence relation that preserves some of the group structure (the rest of the structure is "factored" out). For examp ...
is isomorphic
In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word is ...
to the group . Group extensions arise in the context of the extension problem, where the groups and are known and the properties of are to be determined. Note that the phrasing " is an extension of by " is also used by some.
Since any finite group
Finite is the opposite of infinite. It may refer to:
* Finite number (disambiguation)
* Finite set, a set whose cardinality (number of elements) is some natural number
* Finite verb, a verb form that has a subject, usually being inflected or marked ...
possesses a maximal normal subgroup
In abstract algebra, a normal subgroup (also known as an invariant subgroup or self-conjugate subgroup) is a subgroup that is invariant under conjugation by members of the group of which it is a part. In other words, a subgroup N of the group G i ...
with simple
Simple or SIMPLE may refer to:
*Simplicity, the state or quality of being simple
Arts and entertainment
* ''Simple'' (album), by Andy Yorke, 2008, and its title track
* "Simple" (Florida Georgia Line song), 2018
* "Simple", a song by Johnn ...
factor group , all finite groups may be constructed as a series of extensions with finite simple groups. This fact was a motivation for completing the classification of finite simple groups.
An extension is called a central extension if the subgroup lies in the center of .
Extensions in general
One extension, thedirect product
In mathematics, one can often define a direct product of objects already known, giving a new one. This generalizes the Cartesian product of the underlying sets, together with a suitably defined structure on the product set. More abstractly, one ta ...
, is immediately obvious. If one requires and to be abelian group
In mathematics, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on the order in which they are written. That is, the group operation is commut ...
s, then the set of isomorphism classes of extensions of by a given (abelian) group is in fact a group, which is isomorphic
In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word is ...
to
:
cf. the Ext functor. Several other general classes of extensions are known but no theory exists that treats all the possible extensions at one time. Group extension is usually described as a hard problem; it is termed the extension problem.
To consider some examples, if , then is an extension of both and . More generally, if is a semidirect product
In mathematics, specifically in group theory, the concept of a semidirect product is a generalization of a direct product. There are two closely related concepts of semidirect product:
* an ''inner'' semidirect product is a particular way in w ...
of and , written as , then is an extension of by , so such products as the wreath product provide further examples of extensions.
Extension problem
The question of what groups are extensions of by is called the extension problem, and has been studied heavily since the late nineteenth century. As to its motivation, consider that the composition series of a finite group is a finite sequence of subgroups , where each is an extension of by some simple group. The classification of finite simple groups gives us a complete list of finite simple groups; so the solution to the extension problem would give us enough information to construct and classify all finite groups in general.Classifying extensions
Solving the extension problem amounts to classifying all extensions of ''H'' by ''K''; or more practically, by expressing all such extensions in terms of mathematical objects that are easier to understand and compute. In general, this problem is very hard, and all the most useful results classify extensions that satisfy some additional condition. It is important to know when two extensions are equivalent or congruent. We say that the extensions
:
and
:
are equivalent (or congruent) if there exists a group isomorphism making commutative the diagram of Figure 1.
In fact it is sufficient to have a group homomorphism; due to the assumed commutativity of the diagram, the map is forced to be an isomorphism by the
It is important to know when two extensions are equivalent or congruent. We say that the extensions
:
and
:
are equivalent (or congruent) if there exists a group isomorphism making commutative the diagram of Figure 1.
In fact it is sufficient to have a group homomorphism; due to the assumed commutativity of the diagram, the map is forced to be an isomorphism by the short five lemma
In mathematics, especially homological algebra and other applications of abelian category theory, the short five lemma is a special case of the five lemma.
It states that for the following commutative diagram (in any abelian category, or in the cat ...
.Warning
It may happen that the extensions and are inequivalent but ''G'' and ''G are isomorphic as groups. For instance, there are inequivalent extensions of theKlein four-group
In mathematics, the Klein four-group is a Group (mathematics), group with four elements, in which each element is Involution (mathematics), self-inverse (composing it with itself produces the identity)
and in which composing any two of the three ...
by , but there are, up to group isomorphism, only four groups of order containing a normal subgroup of order with quotient group isomorphic to the Klein four-group
In mathematics, the Klein four-group is a Group (mathematics), group with four elements, in which each element is Involution (mathematics), self-inverse (composing it with itself produces the identity)
and in which composing any two of the three ...
.
Trivial extensions
A trivial extension is an extension : that is equivalent to the extension : where the left and right arrows are respectively the inclusion and the projection of each factor of .Classifying split extensions
A split extension is an extension : with ahomomorphism
In algebra, a homomorphism is a structure-preserving map between two algebraic structures of the same type (such as two groups, two rings, or two vector spaces). The word ''homomorphism'' comes from the Ancient Greek language: () meaning "same" ...
such that going from ''H'' to ''G'' by ''s'' and then back to ''H'' by the quotient map of the short exact sequence induces the identity map
Graph of the identity function on the real numbers
In mathematics, an identity function, also called an identity relation, identity map or identity transformation, is a function that always returns the value that was used as its argument, unch ...
on ''H'' i.e., . In this situation, it is usually said that ''s'' splits the above exact sequence.
Split extensions are very easy to classify, because an extension is split if and only if
In logic and related fields such as mathematics and philosophy, "if and only if" (shortened as "iff") is a biconditional logical connective between statements, where either both statements are true or both are false.
The connective is bicondi ...
the group ''G'' is a semidirect product
In mathematics, specifically in group theory, the concept of a semidirect product is a generalization of a direct product. There are two closely related concepts of semidirect product:
* an ''inner'' semidirect product is a particular way in w ...
of ''K'' and ''H''. Semidirect products themselves are easy to classify, because they are in one-to-one correspondence with homomorphisms from , where Aut(''K'') is the automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms ...
group of ''K''. For a full discussion of why this is true, see semidirect product
In mathematics, specifically in group theory, the concept of a semidirect product is a generalization of a direct product. There are two closely related concepts of semidirect product:
* an ''inner'' semidirect product is a particular way in w ...
.
Warning on terminology
In general in mathematics, an extension of a structure ''K'' is usually regarded as a structure ''L'' of which ''K'' is a substructure. See for examplefield extension
In mathematics, particularly in algebra, a field extension is a pair of fields E\subseteq F, such that the operations of ''E'' are those of ''F'' restricted to ''E''. In this case, ''F'' is an extension field of ''E'' and ''E'' is a subfield of ...
. However, in group theory the opposite terminology has crept in, partly because of the notation , which reads easily as extensions of ''Q'' by ''N'', and the focus is on the group ''Q''.
A paper of Ronald Brown and Timothy Porter on Otto Schreier
Otto Schreier (3 March 1901 in Vienna, Austria – 2 June 1929 in Hamburg, Germany) was a Jewish-Austrian mathematician who made major contributions in combinatorial group theory and in the topology of Lie groups.
Life
His parents were the arc ...
's theory of nonabelian extensions uses the terminology that an extension of ''K'' gives a larger structure.
Central extension
A central extension of a group ''G'' is a short exact sequence of groups : such that ''A'' is included in , the center of the group ''E''. The set of isomorphism classes of central extensions of ''G'' by ''A'' is in one-to-one correspondence with thecohomology
In mathematics, specifically in homology theory and algebraic topology, cohomology is a general term for a sequence of abelian groups, usually one associated with a topological space, often defined from a cochain complex. Cohomology can be viewe ...
group .
Examples of central extensions can be constructed by taking any group ''G'' and any abelian group
In mathematics, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on the order in which they are written. That is, the group operation is commut ...
''A'', and setting ''E'' to be . This kind of ''split'' example corresponds to the element 0 in under the above correspondence. More serious examples are found in the theory of projective representation In the field of representation theory in mathematics, a projective representation of a group ''G'' on a vector space ''V'' over a field ''F'' is a group homomorphism from ''G'' to the projective linear group
\mathrm(V) = \mathrm(V) / F^*,
where GL(' ...
s, in cases where the projective representation cannot be lifted to an ordinary linear representation.
In the case of finite perfect groups, there is a universal perfect central extension.
Similarly, the central extension of a Lie algebra
In mathematics, a Lie algebra (pronounced ) is a vector space \mathfrak g together with an Binary operation, operation called the Lie bracket, an Alternating multilinear map, alternating bilinear map \mathfrak g \times \mathfrak g \rightarrow ...
is an exact sequence
:
such that is in the center of .
There is a general theory of central extensions in Maltsev varieties.
Generalization to general extensions
There is a similar classification of all extensions of ''G'' by ''A'' in terms of homomorphisms from , a tedious but explicitly checkable existence condition involving and the cohomology group .P. J. MorandiGroup Extensions and ''H''3
. From his collection of short mathematical notes.
Lie groups
InLie group
In mathematics, a Lie group (pronounced ) is a group that is also a differentiable manifold. A manifold is a space that locally resembles Euclidean space, whereas groups define the abstract concept of a binary operation along with the additio ...
theory, central extensions arise in connection with algebraic topology
Algebraic topology is a branch of mathematics that uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariant (mathematics), invariants that classification theorem, classify topological spaces up t ...
. Roughly speaking, central extensions of Lie groups by discrete groups are the same as covering groups. More precisely, a connected covering space of a connected Lie group is naturally a central extension of , in such a way that the projection
:
is a group homomorphism, and surjective. (The group structure on depends on the choice of an identity element mapping to the identity in .) For example, when is the universal cover of , the kernel of ''π'' is the fundamental group
In the mathematical field of algebraic topology, the fundamental group of a topological space is the group of the equivalence classes under homotopy of the loops contained in the space. It records information about the basic shape, or holes, of ...
of , which is known to be abelian (see H-space In mathematics, an H-space is a homotopy-theoretic version of a generalization of the notion of topological group, in which the axioms on associativity and inverses are removed.
Definition
An H-space consists of a topological space , together wit ...
). Conversely, given a Lie group and a discrete central subgroup , the quotient is a Lie group and is a covering space of it.
More generally, when the groups , and occurring in a central extension are Lie groups, and the maps between them are homomorphisms of Lie groups, then if the Lie algebra of is , that of is , and that of is , then is a central Lie algebra extension of by . In the terminology of theoretical physics
Theoretical physics is a branch of physics that employs mathematical models and abstractions of physical objects and systems to rationalize, explain and predict natural phenomena. This is in contrast to experimental physics, which uses experim ...
, generators of are called central charges. These generators are in the center of ; by Noether's theorem, generators of symmetry groups correspond to conserved quantities, referred to as charges
Charge or charged may refer to:
Arts, entertainment, and media Films
* ''Charge, Zero Emissions/Maximum Speed'', a 2011 documentary
Music
* ''Charge'' (David Ford album)
* ''Charge'' (Machel Montano album)
* '' Charge!!'', an album by The Aqu ...
.
The basic examples of central extensions as covering groups are:
* the spin group
In mathematics the spin group Spin(''n'') page 15 is the double cover of the special orthogonal group , such that there exists a short exact sequence of Lie groups (when )
:1 \to \mathrm_2 \to \operatorname(n) \to \operatorname(n) \to 1.
As a L ...
s, which double cover the special orthogonal group
In mathematics, the orthogonal group in dimension , denoted , is the group of distance-preserving transformations of a Euclidean space of dimension that preserve a fixed point, where the group operation is given by composing transformations. T ...
s, which (in even dimension) doubly cover the projective orthogonal group In projective geometry and linear algebra, the projective orthogonal group PO is the induced action of the orthogonal group of a quadratic space ''V'' = (''V'',''Q'')A quadratic space is a vector space ''V'' together with a quadratic form ''Q''; ...
.
* the metaplectic group
In mathematics, the metaplectic group Mp2''n'' is a double cover of the symplectic group Sp2''n''. It can be defined over either real or ''p''-adic numbers. The construction covers more generally the case of an arbitrary local or finite field, ...
s, which double cover the symplectic groups.
The case of involves a fundamental group that is infinite cyclic. Here the central extension involved is well known in modular form
In mathematics, a modular form is a (complex) analytic function on the upper half-plane satisfying a certain kind of functional equation with respect to the Group action (mathematics), group action of the modular group, and also satisfying a grow ...
theory, in the case of forms of weight . A projective representation that corresponds is the Weil representation, constructed from the Fourier transform
A Fourier transform (FT) is a mathematical transform that decomposes functions into frequency components, which are represented by the output of the transform as a function of frequency. Most commonly functions of time or space are transformed, ...
, in this case on the real line
In elementary mathematics, a number line is a picture of a graduated straight line (geometry), line that serves as visual representation of the real numbers. Every point of a number line is assumed to correspond to a real number, and every real ...
. Metaplectic groups also occur in quantum mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, ...
.
See also
*Lie algebra extension
In the theory of Lie groups, Lie algebras and their representation theory, a Lie algebra extension is an enlargement of a given Lie algebra by another Lie algebra . Extensions arise in several ways. There is the trivial extension obtained by ta ...
* Ring extension
* Virasoro algebra
*HNN extension In mathematics, the HNN extension is an important construction of combinatorial group theory.
Introduced in a 1949 paper ''Embedding Theorems for Groups'' by Graham Higman, Bernhard Neumann, and Hanna Neumann, it embeds a given group ''G'' into an ...
*Group contraction
In theoretical physics, Eugene Wigner and Erdal İnönü have discussed the possibility to obtain from a given Lie group a different (non-isomorphic) Lie group by a group contraction with respect to a continuous subgroup of it. That amounts to a ...
*Extension of a topological group In mathematics, more specifically in topological groups, an extension of topological groups, or a topological extension, is a short exact sequence 0\to H\stackrel X \stackrelG\to 0 where H, X and G are topological groups and i and \pi are co ...
References
*{{Citation , first=Saunders , last1=Mac Lane , authorlink = Saunders Mac Lane, title=Homology , publisher=Springer Verlag
Springer Science+Business Media, commonly known as Springer, is a German multinational publishing company of books, e-books and peer-reviewed journals in science, humanities, technical and medical (STM) publishing.
Originally founded in 1842 in ...
, year=1975 , isbn=3-540-58662-8 , series=Classics in Mathematics
* R.L. Taylor, Covering groups of non connected topological groups, ''Proceedings of the American Mathematical Society
''Proceedings of the American Mathematical Society'' is a monthly peer-reviewed scientific journal of mathematics published by the American Mathematical Society. As a requirement, all articles must be at most 15 printed pages.
According to the ' ...
'', vol. 5 (1954), 753–768.
* R. Brown and O. Mucuk, Covering groups of non-connected topological groups revisited, ''Mathematical Proceedings of the Cambridge Philosophical Society
''Mathematical Proceedings of the Cambridge Philosophical Society'' is a mathematical journal published by Cambridge University Press for the Cambridge Philosophical Society. It aims to publish original research papers from a wide range of pure a ...
'', vol. 115 (1994), 97–110.
Group theory