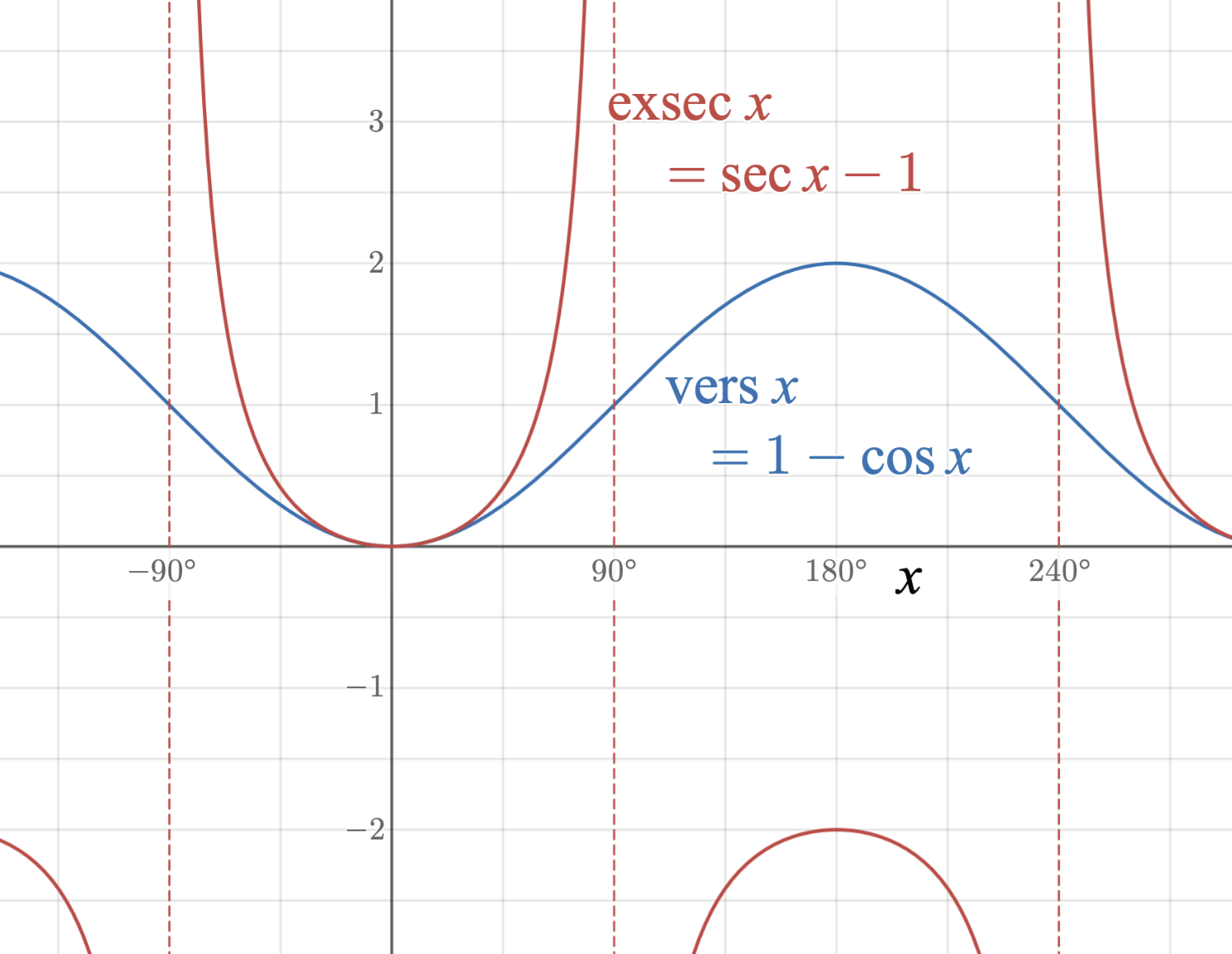The external secant function (abbreviated exsecant, symbolized exsec) is a

trigonometric function In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all ...

defined in terms of the secant function:

\operatorname \theta = \sec\theta - 1 = \frac - 1.

It was introduced in 1855 by American

civil engineer A civil engineer is a person who practices civil engineering – the application of planning, designing, constructing, maintaining, and operating infrastructure while protecting the public and environmental health, as well as improving existing i ...

Charles Haslett, who used it in conjunction with the existing

versine The versine or versed sine is a trigonometric function found in some of the earliest (Sanskrit ''Aryabhatia'',circular sections of

railroad Rail transport (also known as train transport) is a means of transport using wheeled vehicles running in railway track, tracks, which usually consist of two parallel steel railway track, rails. Rail transport is one of the two primary means of ...

track. It was adopted by surveyors and civil engineers in the United States for railroad and road design, and since the early 20th century has sometimes been briefly mentioned in American trigonometry textbooks and general-purpose engineering manuals. For completeness, a few books also defined a coexsecant or excosecant function (symbolized coexsec or excsc),

\operatorname \theta =

\csc\theta - 1,

the exsecant of the complementary angle, though it was not used in practice. While the exsecant has occasionally found other applications, today it is obscure and mainly of historical interest. As a

line segment In geometry, a line segment is a part of a line (mathematics), straight line that is bounded by two distinct endpoints (its extreme points), and contains every Point (geometry), point on the line that is between its endpoints. It is a special c ...

, an external secant of a

circle A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...

has one endpoint on the circumference, and then extends radially outward. The length of this segment is the radius of the circle times the trigonometric exsecant of the central angle between the segment's inner endpoint and the point of tangency for a line through the outer endpoint and

tangent In geometry, the tangent line (or simply tangent) to a plane curve at a given point is, intuitively, the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points o ...

to the circle.

Etymology

The word ''secant'' comes from Latin for "to cut", and a general

secant line In geometry, a secant is a line (geometry), line that intersects a curve at a minimum of two distinct Point (geometry), points.. The word ''secant'' comes from the Latin word ''secare'', meaning ''to cut''. In the case of a circle, a secant inter ...

"cuts" a circle, intersecting it twice; this concept dates to antiquity and can be found in Book 3 of Euclid's ''Elements'', as used e.g. in the intersecting secants theorem. 18th century sources in

Latin Latin ( or ) is a classical language belonging to the Italic languages, Italic branch of the Indo-European languages. Latin was originally spoken by the Latins (Italic tribe), Latins in Latium (now known as Lazio), the lower Tiber area aroun ...

called ''any'' non-

ial line segment external to a circle with one endpoint on the circumference a ''secans exterior''. The trigonometric ''secant'', named by Thomas Fincke (1583), is more specifically based on a line segment with one endpoint at the center of a circle and the other endpoint outside the circle; the circle divides this segment into a radius and an external secant. The external secant segment was used by

Galileo Galilei Galileo di Vincenzo Bonaiuti de' Galilei (15 February 1564 – 8 January 1642), commonly referred to as Galileo Galilei ( , , ) or mononymously as Galileo, was an Italian astronomer, physicist and engineer, sometimes described as a poly ...

(1632) under the name ''secant''.

History and applications

In the 19th century, most

tracks were constructed out of arcs of circles, called ''simple curves''. Surveyors and civil engineers working for the railroad needed to make many repetitive trigonometrical calculations to measure and plan circular sections of track. In surveying, and more generally in practical geometry, tables of both "natural" trigonometric functions and their

common logarithm In mathematics, the common logarithm (aka "standard logarithm") is the logarithm with base 10. It is also known as the decadic logarithm, the decimal logarithm and the Briggsian logarithm. The name "Briggsian logarithm" is in honor of the British ...

s were used, depending on the specific calculation. Using logarithms converts expensive multiplication of multi-digit numbers to cheaper addition, and logarithmic versions of trigonometric tables further saved labor by reducing the number of necessary table lookups. The ''external secant'' or ''external distance'' of a curved track section is the shortest distance between the track and the intersection of the tangent lines from the ends of the arc, which equals the radius times the trigonometric exsecant of half the

central angle A central angle is an angle whose apex (vertex) is the center O of a circle and whose legs (sides) are radii intersecting the circle in two distinct points A and B. Central angles are subtended by an arc between those two points, and the arc l ...

subtended by the arc,

R\operatorname\tfrac12\Delta.

By comparison, the ''versed sine'' of a curved track section is the furthest distance from the ''long chord'' (the line segment between endpoints) to the track – cf.

Sagitta Sagitta is a dim but distinctive constellation in the northern sky. Its name is Latin for 'arrow', not to be confused with the significantly larger constellation Sagittarius 'the archer'. It was included among the 48 constellations listed by t ...

– which equals the radius times the trigonometric versine of half the central angle,

R\operatorname\tfrac12\Delta.

These are both natural quantities to measure or calculate when surveying circular arcs, which must subsequently be multiplied or divided by other quantities. Charles Haslett (1855) found that directly looking up the logarithm of the exsecant and versine saved significant effort and produced more accurate results compared to calculating the same quantity from values found in previously available trigonometric tables. The same idea was adopted by other authors, such as Searles (1880). By 1913 Haslett's approach was so widely adopted in the American railroad industry that, in that context, "tables of external secants and versed sines

ere Ere or ERE may refer to: * ''Environmental and Resource Economics'', a peer-reviewed academic journal * ERE Informatique, one of the first French video game companies * Ere language, an Austronesian language * Ebi Ere (born 1981), American-Nigeria ...

more common than

tables of secants". In the late-19th and 20th century, railroads began using arcs of an

Euler spiral An Euler spiral is a curve whose curvature changes linearly with its curve length (the curvature of a circular curve is equal to the reciprocal of the radius). This curve is also referred to as a clothoid or Cornu spiral.Levien, Raph"The Euler spi ...

as a

track transition curve A transition curve (also, spiral easement or, simply, spiral) is a spiral-shaped length of highway or track (rail transport), railroad track that is used between sections having different profiles and radii, such as between straightaways (tangen ...

between straight or circular sections of differing curvature. These spiral curves can be approximately calculated using exsecants and versines. Solving the same types of problems is required when surveying circular sections of

canal Canals or artificial waterways are waterways or engineered channels built for drainage management (e.g. flood control and irrigation) or for conveyancing water transport vehicles (e.g. water taxi). They carry free, calm surface ...

s and roads, and the exsecant was still used in mid-20th century books about road surveying. The exsecant has sometimes been used for other applications, such as

beam theory Beam may refer to: Streams of particles or energy *Light beam, or beam of light, a directional projection of light energy **Laser beam * Radio beam *Particle beam, a stream of charged or neutral particles ** Charged particle beam, a spatially ...

and

depth sounding Depth sounding, often simply called sounding, is measuring the depth of a body of water. Data taken from soundings are used in bathymetry to make maps of the floor of a body of water, such as the seabed topography. Soundings were traditional ...

with a wire. In recent years, the availability of

calculator An electronic calculator is typically a portable electronic device used to perform calculations, ranging from basic arithmetic to complex mathematics. The first solid-state electronic calculator was created in the early 1960s. Pocket-si ...

s and

computer A computer is a machine that can be Computer programming, programmed to automatically Execution (computing), carry out sequences of arithmetic or logical operations (''computation''). Modern digital electronic computers can perform generic set ...

s has removed the need for trigonometric tables of specialized functions such as this one. Exsecant is generally not directly built into calculators or computing environments (though it has sometimes been included in

software libraries In computing, a library is a collection of resources that can be leveraged during software development to implement a computer program. Commonly, a library consists of executable code such as compiled functions and classes, or a library can ...

), and calculations in general are much cheaper than in the past, no longer requiring tedious manual labor.

Catastrophic cancellation for small angles

Naïvely evaluating the expressions

1 - \cos \theta

(versine) and

\sec \theta - 1

(exsecant) is problematic for small angles where

\sec \theta \approx \cos \theta \approx 1.

Computing the difference between two approximately equal quantities results in

catastrophic cancellation In numerical analysis, catastrophic cancellation is the phenomenon that subtracting good approximations to two nearby numbers may yield a very bad approximation to the difference of the original numbers. For example, if there are two studs, one L ...

: because most of the digits of each quantity are the same, they cancel in the subtraction, yielding a lower-precision result. For example, the secant of is approximately , with the leading several digits wasted on zeros, while the

of the exsecant of is approximately , all of whose digits are meaningful. If the logarithm of exsecant is calculated by looking up the secant in a six-place trigonometric table and then subtracting , the difference has only 3

significant digits Significant figures, also referred to as significant digits, are specific digits within a number that is written in positional notation that carry both reliability and necessity in conveying a particular quantity. When presenting the outcom ...

, and after computing the logarithm only three digits are correct, .The incorrect digits are highlighted in red. For even smaller angles loss of precision is worse. If a table or computer implementation of the exsecant function is not available, the exsecant can be accurately computed as

\operatorname \theta = \tan \theta \, \tan \tfrac12\theta\vphantom\Big, ,

or using versine,

\operatorname \theta = \operatorname \theta \, \sec \theta,

which can itself be computed as

\operatorname \theta  = 2 \bigl(\bigr)\vphantom)^2\vphantom\Big,  =

Haslett used these identities to compute his 1855 exsecant and versine tables. For a sufficiently small angle, a circular arc is approximately shaped like a

parabola In mathematics, a parabola is a plane curve which is Reflection symmetry, mirror-symmetrical and is approximately U-shaped. It fits several superficially different Mathematics, mathematical descriptions, which can all be proved to define exactl ...

, and the versine and exsecant are approximately equal to each-other and both proportional to the square of the arclength.

Mathematical identities

Inverse function

The inverse of the exsecant function, which might be symbolized , is well defined if its argument

y \geq 0

y \leq -2

and can be expressed in terms of other

inverse trigonometric function In mathematics, the inverse trigonometric functions (occasionally also called ''antitrigonometric'', ''cyclometric'', or ''arcus'' functions) are the inverse functions of the trigonometric functions, under suitably restricted domains. Specific ...

s (using

radian The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. It is defined such that one radian is the angle subtended at ...

s for the angle):

\pi - \bigl(\!\,\bigr) & \text\ \ y \leq ; \\ \end_

the arctangent expression is well behaved for small angles.

Calculus

While historical uses of the exsecant did not explicitly involve

calculus Calculus is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations. Originally called infinitesimal calculus or "the ...

, its

derivative In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is t ...

and

antiderivative In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a continuous function is a differentiable function whose derivative is equal to the original function . This can be stated ...

(for in radians) are:

\int\operatorname x\,\mathrmx &= \ln\bigl, \sec x + \tan x\bigr, - x + C,\vphantom \end

where is the

natural logarithm The natural logarithm of a number is its logarithm to the base of a logarithm, base of the e (mathematical constant), mathematical constant , which is an Irrational number, irrational and Transcendental number, transcendental number approxima ...

. See also Integral of the secant function.

Double angle identity

The exsecant of twice an angle is:

\operatorname 2\theta = \frac .

Notes and references

{{Trigonometric and hyperbolic functions Trigonometric functions