Euler Buckling

Euler's critical load or Euler's buckling load is the compressive load at which a slender column will suddenly bend or buckle. It is given by the formula:

$P_ = \frac$

where
*$P_$, Euler's critical load (longitudinal compression load on column),
*$E$, Young's modulus of the column material,
*$I$, minimum second moment of area of the cross section of the column (area moment of inertia),
*$L$, unsupported length of column,
*$K$, column effective length factor

This formula was derived in 1744 by the Swiss mathematician Leonhard Euler. The column will remain straight for loads less than the critical load. The ''critical load'' is the greatest load that will not cause lateral deflection (buckling). For loads greater than the critical load, the column will deflect laterally. The critical load puts the column in a state of unstable equilibrium. A load beyond the critical load causes the column to fail by buckling. As the load is increased beyond the critical load the lateral deflections increase, until it may fail in other modes such as yielding of the material. Loading of columns beyond the critical load are not addressed in this article.

Johnson's parabolic formula, an alternative used for low slenderness ratios was constructed by John Butler Johnson (1850–1902) in 1893.

Assumptions of the model

The following assumptions are made while deriving Euler's formula:
# The material of the column is homogeneous and isotropic.
# The compressive load on the column is axial only.
# The column is free from initial stress.
# The weight of the column is neglected.
# The column is initially straight (no eccentricity of the axial load).
# Pin joints are friction-less (no moment constraint) and fixed ends are rigid (no rotation deflection).
# The cross-section of the column is uniform throughout its length.
# The direct stress is very small as compared to the bending stress (the material is compressed only within the elastic range of strains).
# The length of the column is very large as compared to the cross-sectional dimensions of the column.
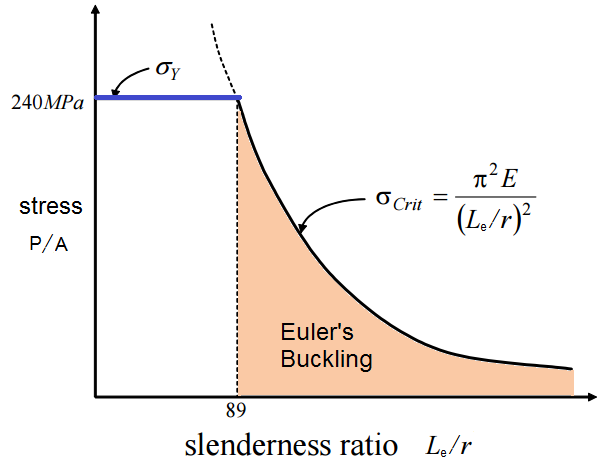
# The column fails only by buckling. This is true if the compressive stress in the column does not exceed the yield strength $\sigma_y$ (see figure 1): $\sigma = \frac = \frac < \sigma_y$ where:
#* $/$ is the slenderness ratio,
#* $L_e = KL$ is the effective length,
#* $r = \sqrt$ is the radius of gyration,
#* $I$ is the second moment of area (area moment of inertia),
#* $A$ is the area cross section.

For slender columns, the critical buckling stress is usually lower than the yield stress. In contrast, a stocky column can have a critical buckling stress higher than the yield, i.e. it yields prior to buckling.

Mathematical derivation

Pin ended column

The following model applies to columns simply supported at each end ($K = 1$).

Firstly, we will put attention to the fact there are no reactions in the hinged ends, so we also have no shear force in any cross-section of the column. The reason for no reactions can be obtained from symmetry (so the reactions should be in the same direction) and from moment equilibrium (so the reactions should be in opposite directions).

Using the free body diagram in the right side of figure 3, and making a summation of moments about point :
$\Sigma M = 0 \Rightarrow M(x) + Pw = 0$
where is the lateral deflection.

According to Euler–Bernoulli beam theory, the deflection of a beam is related with its bending moment by:
$M = -EI\frac.$

so:
$EI\frac + Pw = 0$

Let $\lambda^2 = \frac$, so:
$\frac + \lambda^2 w = 0$

We get a classical homogeneous second-order ordinary differential equation.

The general solutions of this equation is: $w(x) = A \cos(\lambda x) + B \sin(\lambda x)$, where $A$ and $B$ are constants to be determined by boundary conditions, which are:
* Left end pinned: $w(0) = 0 \rightarrow A = 0$
* Right end pinned: $w(\ell) = 0 \rightarrow B \sin(\lambda \ell) = 0$

If $B = 0$, no bending moment exists and we get the trivial solution of $w(x) = 0$.

However, from the other solution $\sin(\lambda \ell) = 0$ we get $\lambda_n \ell = n\pi$, for $n = 0, 1, 2, \ldots$

Together with $\lambda^2 = \frac$ as defined before, the various critical loads are:
$P_ = \frac \; , \quad \text n = 0, 1, 2, \ldots$
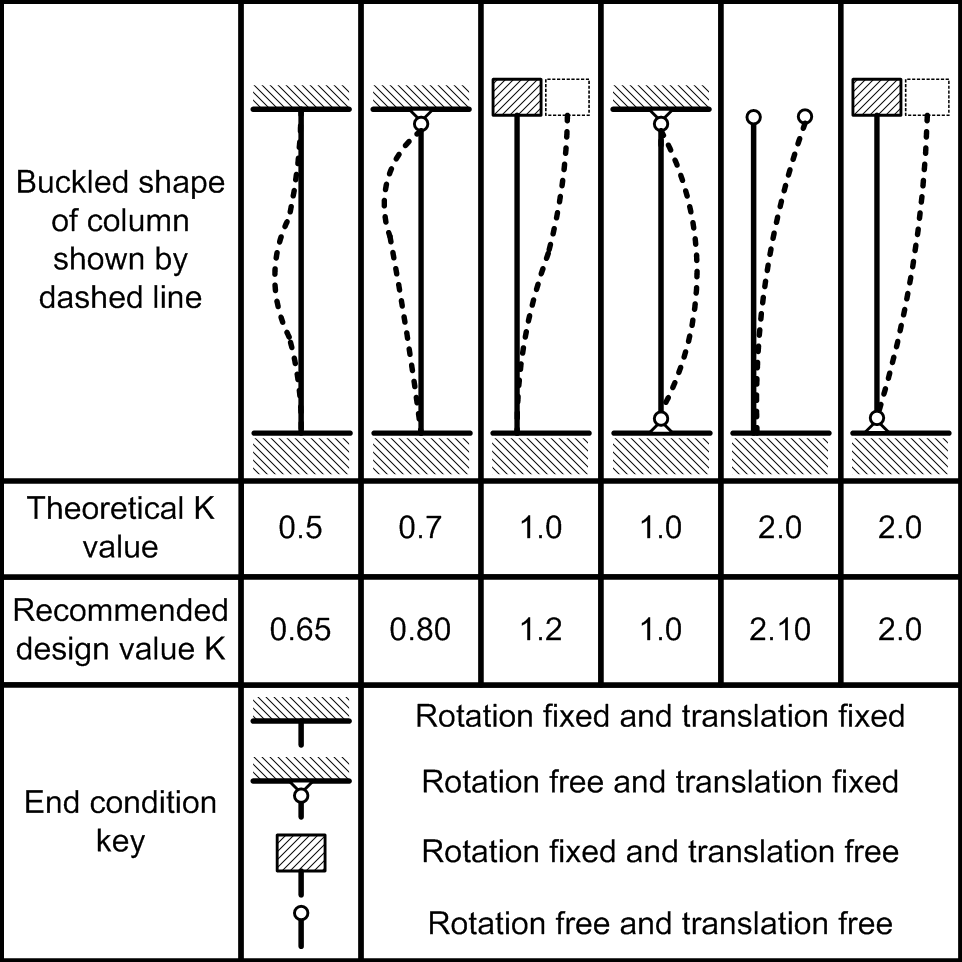
and depending upon the value of $n$, different buckling modes are produced as shown in figure 4. The load and mode for n=0 is the nonbuckled mode.

Theoretically, any buckling mode is possible, but in the case of a slowly applied load only the first modal shape is likely to be produced.

The critical load of Euler for a pin ended column is therefore:
$P_ = \frac$
and the obtained shape of the buckled column in the first mode is:
$w(x) = B \sin \left( x\right) .$

General approach

The differential equation of the axis of a beam is:
$\frac + \frac\frac = \frac$

For a column with axial load only, the lateral load $q(x)$ vanishes and substituting $\lambda^2 = \frac$, we get:
$\frac + \lambda^2\frac = 0$

This is a homogeneous fourth-order differential equation and its general solution is
$w(x) = A\sin(\lambda x) + B\cos(\lambda x) + Cx + D$

The four constants $A, B, C, D$ are determined by the boundary conditions (end constraints) on $w(x)$, at each end. There are three cases:
# Pinned end:
#: $w = 0$ and $M = 0 \rightarrow = 0$
# Fixed end:
#: $w = 0$ and $= 0$
# Free end:
#: $M = 0 \rightarrow = 0$ and $V = 0 \rightarrow + \lambda^2 = 0$

For each combination of these boundary conditions, an eigenvalue problem is obtained. Solving those, we get the values of Euler's critical load for each one of the cases presented in Figure 2.

See also

* Buckling
* Bending moment
* Bending
* Euler–Bernoulli beam theory

References

{{Leonhard Euler

Elasticity (physics)
Mechanical failure modes
Structural analysis
Mechanics
Leonhard Euler