Etendue on:
[Wikipedia]
[Google]
[Amazon]
Etendue or étendue (; ) is a property of
 An infinitesimal surface element, dS, with normal n''S'' is immersed in a medium of
An infinitesimal surface element, dS, with normal n''S'' is immersed in a medium of
list of view factors for specific geometry cases
or in several
 The conservation of etendue discussed above applies to the case of light propagation in free space, or more generally, in a medium of any
The conservation of etendue discussed above applies to the case of light propagation in free space, or more generally, in a medium of any
Solid Angle and the Brightness Theorem
Appendix A, ''Photonics and Lasers: An Introduction'', Wiley Science Library. https://doi.org/10.1002/0471791598.app1. Retrieved 13 Sept 2022.
 In the context of
In the context of
 Consider an infinitesimal surface d''S'', immersed in a medium of refractive index ''n'' crossed by (or emitting) light inside a cone of angle ''α''. The etendue of this light is given by
Noting that ''n'' sin ''α'' is the numerical aperture ''NA'', of the beam of light, this can also be expressed as
Note that d''Ω'' is expressed in a
Consider an infinitesimal surface d''S'', immersed in a medium of refractive index ''n'' crossed by (or emitting) light inside a cone of angle ''α''. The etendue of this light is given by
Noting that ''n'' sin ''α'' is the numerical aperture ''NA'', of the beam of light, this can also be expressed as
Note that d''Ω'' is expressed in a  The limit on maximum concentration (shown) is an optic with an entrance aperture ''S'', in air () collecting light within a solid angle of angle 2''α'' (its acceptance angle) and sending it to a smaller area receiver ''Σ'' immersed in a medium of refractive index ''n'', whose points are illuminated within a solid angle of angle 2''β''. From the above expression, the etendue of the incoming light is
and the etendue of the light reaching the receiver is
Conservation of etendue then gives
where ''C'' is the concentration of the optic. For a given angular aperture ''α'', of the incoming light, this concentration will be maximum for the maximum value of sin ''β'', that is ''β'' = π/2. The maximum possible concentration is then
In the case that the incident index is not unity, we have
and so
and in the best-case limit of ''β'' = π/2, this becomes
If the optic were a
The limit on maximum concentration (shown) is an optic with an entrance aperture ''S'', in air () collecting light within a solid angle of angle 2''α'' (its acceptance angle) and sending it to a smaller area receiver ''Σ'' immersed in a medium of refractive index ''n'', whose points are illuminated within a solid angle of angle 2''β''. From the above expression, the etendue of the incoming light is
and the etendue of the light reaching the receiver is
Conservation of etendue then gives
where ''C'' is the concentration of the optic. For a given angular aperture ''α'', of the incoming light, this concentration will be maximum for the maximum value of sin ''β'', that is ''β'' = π/2. The maximum possible concentration is then
In the case that the incident index is not unity, we have
and so
and in the best-case limit of ''β'' = π/2, this becomes
If the optic were a
light
Light or visible light is electromagnetic radiation that can be perceived by the human eye. Visible light is usually defined as having wavelengths in the range of 400–700 nanometres (nm), corresponding to frequencies of 750–420 tera ...
in an optical system
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behaviour of visible, ultravio ...
, which characterizes how "spread out" the light is in area and angle. It corresponds to the beam parameter product In laser science, the beam parameter product (BPP) is the product of a laser beam's divergence angle (half-angle) and the radius of the beam at its narrowest point (the beam waist). The BPP quantifies the quality of a laser beam, and how well it can ...
(BPP) in Gaussian beam
In optics, a Gaussian beam is a beam of electromagnetic radiation with high monochromaticity whose amplitude envelope in the transverse plane is given by a Gaussian function; this also implies a Gaussian intensity (irradiance) profile. Thi ...
optics. Other names for etendue include acceptance, throughput, light grasp, light-gathering power, optical extent, and the AΩ product. ''Throughput'' and ''AΩ product'' are especially used in radiometry and radiative transfer where it is related to the view factor
In radiative heat transfer, a view factor, F_, is the proportion of the radiation which leaves surface A that strikes surface B. In a complex 'scene' there can be any number of different objects, which can be divided in turn into even more surface ...
(or shape factor). It is a central concept in nonimaging optics Nonimaging optics (also called anidolic optics)Roland Winston et al., ''Nonimaging Optics'', Academic Press, 2004 R. John Koshel (Editor), ''Illumination Engineering: Design with Nonimaging Optics'', Wiley, 2013 is the branch of optics concerned wi ...
.Roland Winston et al.,, ''Nonimaging Optics'', Academic Press, 2004 Matthew S. Brennesholtz, Edward H. Stupp, ''Projection Displays'', John Wiley & Sons Ltd, 2008
From the source point of view, etendue is the product of the area of the source and the solid angle
In geometry, a solid angle (symbol: ) is a measure of the amount of the field of view from some particular point that a given object covers. That is, it is a measure of how large the object appears to an observer looking from that point.
The poi ...
that the system's entrance pupil
In an optical system, the entrance pupil is the optical image of the physical aperture stop, as 'seen' through the front (the object side) of the lens system. The corresponding image of the aperture as seen through the back of the lens system is ...
subtends as seen from the source. Equivalently, from the system point of view, the etendue equals the area of the entrance pupil times the solid angle the source subtends as seen from the pupil. These definitions must be applied for infinitesimally small "elements" of area and solid angle, which must then be summed over both the source and the diaphragm as shown below. Etendue may be considered to be a volume in phase space.
Etendue never decreases in any optical system where optical power is conserved. A perfect optical system produces an image with the same etendue as the source. The etendue is related to the Lagrange invariant
In optics the Lagrange invariant is a measure of the light propagating through an optical system. It is defined by
:H = n\overliney - nu\overline,
where and are the marginal ray height and angle respectively, and and are the chief ray height ...
and the optical invariant
In optics the Lagrange invariant is a measure of the light propagating through an optical system. It is defined by
:H = n\overliney - nu\overline,
where and are the marginal ray height and angle respectively, and and are the chief ray heigh ...
, which share the property of being constant in an ideal optical system. The radiance
In radiometry, radiance is the radiant flux emitted, reflected, transmitted or received by a given surface, per unit solid angle per unit projected area. Radiance is used to characterize diffuse emission and reflection of electromagnetic radiati ...
of an optical system is equal to the derivative of the radiant flux with respect to the etendue.
Definition
 An infinitesimal surface element, dS, with normal n''S'' is immersed in a medium of
An infinitesimal surface element, dS, with normal n''S'' is immersed in a medium of refractive index
In optics, the refractive index (or refraction index) of an optical medium is a dimensionless number that gives the indication of the light bending ability of that medium.
The refractive index determines how much the path of light is bent, or ...
''n''. The surface is crossed by (or emits) light confined to a solid angle, d''Ω'', at an angle ''θ'' with the normal n''S''. The area of d''S'' projected in the direction of the light propagation is . The etendue of an infinitesimal bundle of light crossing dS is defined as
Etendue is the product of geometric extent and the squared refractive index of a medium through which the beam propagates.
Because angles, solid angles, and refractive indices are dimensionless quantities
A dimensionless quantity (also known as a bare quantity, pure quantity, or scalar quantity as well as quantity of dimension one) is a quantity to which no physical dimension is assigned, with a corresponding SI unit of measurement of one (or 1) ...
, etendue is often expressed in units of area (given by dS). However, it can alternatively be expressed in units of area (square meters) multiplied by solid angle (steradians).
In free space
Consider a light source ''Σ'', and a light detector ''S'', both of which are extended surfaces (rather than differential elements), and which are separated by amedium
Medium may refer to:
Science and technology
Aviation
*Medium bomber, a class of war plane
*Tecma Medium, a French hang glider design
Communication
* Media (communication), tools used to store and deliver information or data
* Medium of ...
of refractive index ''n'' that is perfectly transparent
Transparency, transparence or transparent most often refer to:
* Transparency (optics), the physical property of allowing the transmission of light through a material
They may also refer to:
Literal uses
* Transparency (photography), a still, ...
(shown). To compute the etendue of the system, one must consider the contribution of each point on the surface of the light source as they cast rays to each point on the receiver. ''Wikilivre de Photographie'', ''Notion d'étendue géométrique'' (in French). Accessed 27 Jan 2009.
According to the definition above, the etendue of the light crossing d''Σ'' towards d''S'' is given by:
where d''Ω''Σ is the solid angle defined by area d''S'' at area d''Σ'', and ''d'' is the distance between the two areas. Similarly, the etendue of the light crossing d''S'' coming from d''Σ'' is given by:
where d''Ω''''S'' is the solid angle defined by area dΣ. These expressions result in
showing that etendue is conserved as light propagates in free space.
The etendue of the whole system is then:
If both surfaces d''Σ'' and d''S'' are immersed in air (or in vacuum), and the expression above for the etendue may be written as
where ''F''d''Σ''→d''S'' is the view factor
In radiative heat transfer, a view factor, F_, is the proportion of the radiation which leaves surface A that strikes surface B. In a complex 'scene' there can be any number of different objects, which can be divided in turn into even more surface ...
between differential surfaces d''Σ'' and d''S''. Integration on d''Σ'' and d''S'' results in ''G'' = π''Σ'' ''F''''Σ''→''S'' which allows the etendue between two surfaces to be obtained from the view factors between those surfaces, as provided in list of view factors for specific geometry cases
or in several
heat transfer
Heat transfer is a discipline of thermal engineering that concerns the generation, use, conversion, and exchange of thermal energy (heat) between physical systems. Heat transfer is classified into various mechanisms, such as thermal conduction, ...
textbooks.
Conservation of etendue
The etendue of a given bundle of light is conserved: etendue can be increased, but not decreased in any optical system. This means that any system that concentrates light from some source onto a smaller area must always increase the solid angle of incidence (that is, the area of the sky that the source subtends). For example, a magnifying glass can increase the intensity of sunlight onto a small spot, but does so because, viewed from the spot that the light is concentrated onto, the apparent size of the sun is increased proportional to the concentration. As shown below, etendue is conserved as light travels through free space and at refractions or reflections. It is then also conserved as light travels through optical systems where it undergoes perfect reflections or refractions. However, if light was to hit, say, adiffuser
Diffuser may refer to:
Aerodynamics
* Diffuser (automotive), a shaped section of a car's underbody which improves the car's aerodynamic properties
* Part of a jet engine air intake, especially when operated at supersonic speeds
* The channel bet ...
, its solid angle would increase, increasing the etendue. Etendue can then remain constant or it can increase as light propagates through an optic, but it cannot decrease. This is a direct result of the fact that entropy
Entropy is a scientific concept, as well as a measurable physical property, that is most commonly associated with a state of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynam ...
must be constant or increasing.
Conservation of etendue can be derived in different contexts, such as from optical first principles, from Hamiltonian optics Hamiltonian opticsH. A. Buchdahl, ''An Introduction to Hamiltonian Optics'', Dover Publications, 1993, . and Lagrangian opticsVasudevan Lakshminarayanan et al., ''Lagrangian Optics'', Springer Netherlands, 2011, . are two formulations of geometrical ...
or from the second law of thermodynamics
The second law of thermodynamics is a physical law based on universal experience concerning heat and energy interconversions. One simple statement of the law is that heat always moves from hotter objects to colder objects (or "downhill"), unles ...
.
The conservation of etendue in free space is related to the reciprocity theorem for view factors.
In refractions and reflections
 The conservation of etendue discussed above applies to the case of light propagation in free space, or more generally, in a medium of any
The conservation of etendue discussed above applies to the case of light propagation in free space, or more generally, in a medium of any refractive index
In optics, the refractive index (or refraction index) of an optical medium is a dimensionless number that gives the indication of the light bending ability of that medium.
The refractive index determines how much the path of light is bent, or ...
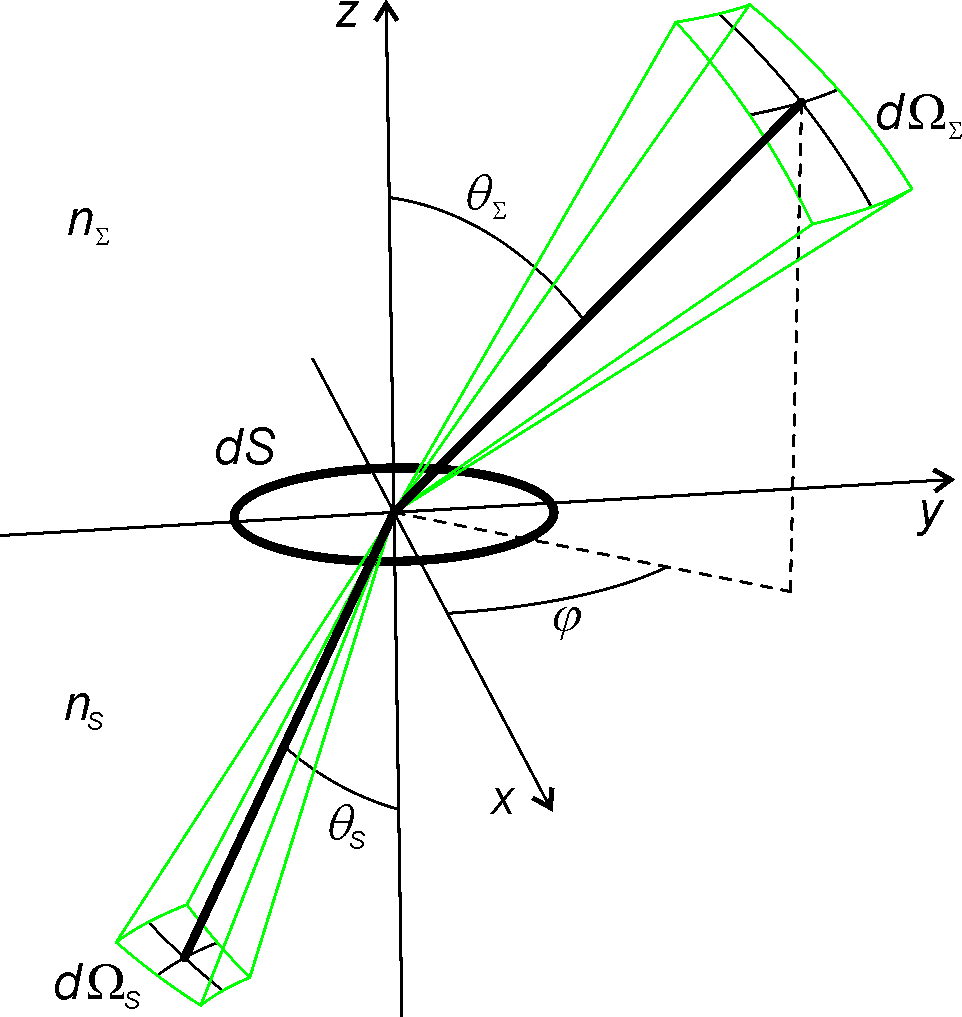
. In particular, etendue is conserved in refractions and reflections. Figure "etendue in refraction" shows an infinitesimal surface d''S'' on the ''xy'' plane separating two media of refractive indices ''n''''Σ'' and ''n''''S''.
The normal to d''S'' points in the direction of the ''z'' axis. Incoming light is confined to a solid angle d''Ω''''Σ'' and reaches d''S'' at an angle ''θ''''Σ'' to its normal. Refracted light is confined to a solid angle d''Ω''''S'' and leaves d''S'' at an angle ''θ''''S'' to its normal. The directions of the incoming and refracted light are contained in a plane making an angle ''φ'' to the ''x'' axis, defining these directions in a spherical coordinate system
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the ''radial distance'' of that point from a fixed origin, its ''polar angle'' measu ...
. With these definitions, Snell's law of refraction can be written as
and its derivative relative to ''θ''
multiplied by each other result in
where both sides of the equation were also multiplied by d''φ'' which does not change on refraction. This expression can now be written as
and multiplying both sides by d''S'' we get
that is
showing that the etendue of the light refracted at d''S'' is conserved. The same result is also valid for the case of a reflection at a surface d''S'', in which case and ''θ''''Σ'' = ''θ''S.
Brightness theorem
A consequence of the conserveration of etendue is the ''brightness theorem'', which states that no optical system can increase thebrightness
Brightness is an attribute of visual perception in which a source appears to be radiating or reflecting light. In other words, brightness is the perception elicited by the luminance of a visual target. The perception is not linear to luminance, ...
of the light emitted from a source to a higher value than the brightness of the surface of that source (where "brightness" is defined as the optical power emitted per unit solid angle per unit emitting or receiving area).Quimby, R. S. (17 March 2006),Solid Angle and the Brightness Theorem
Appendix A, ''Photonics and Lasers: An Introduction'', Wiley Science Library. https://doi.org/10.1002/0471791598.app1. Retrieved 13 Sept 2022.
Conservation of basic radiance
Radiance
In radiometry, radiance is the radiant flux emitted, reflected, transmitted or received by a given surface, per unit solid angle per unit projected area. Radiance is used to characterize diffuse emission and reflection of electromagnetic radiati ...
of a surface is related to étendue by:
where
* is the radiant flux emitted, reflected, transmitted or received;
*''n'' is the refractive index in which that surface is immersed;
*''G'' is the étendue of the light beam.
As the light travels through an ideal optical system, both the étendue and the radiant flux are conserved. Therefore, ''basic radiance'' defined as:William Ross McCluney, ''Introduction to Radiometry and Photometry'', Artech House, Boston, MA, 1994
is also conserved. In real systems, the étendue may increase (for example due to scattering) or the radiant flux may decrease (for example due to absorption) and, therefore, basic radiance may decrease. However, étendue may not decrease and radiant flux may not increase and, therefore, basic radiance may not increase.
Etendue as a volume in phase space
 In the context of
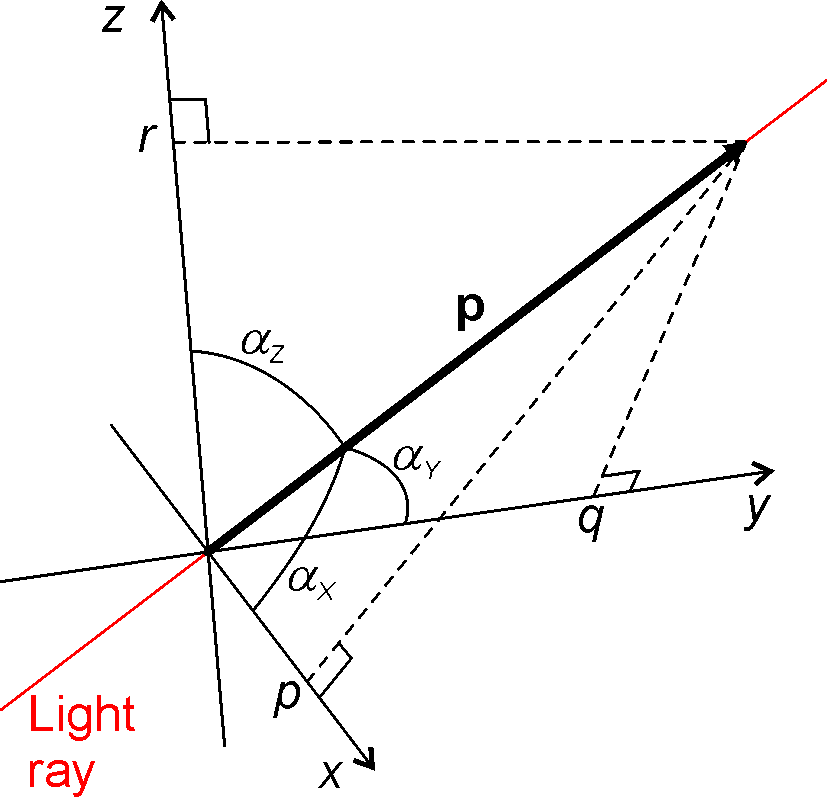
In the context of Hamiltonian optics Hamiltonian opticsH. A. Buchdahl, ''An Introduction to Hamiltonian Optics'', Dover Publications, 1993, . and Lagrangian opticsVasudevan Lakshminarayanan et al., ''Lagrangian Optics'', Springer Netherlands, 2011, . are two formulations of geometrical ...
, at a point in space, a light ray may be completely defined by a point , a unit Euclidean vector
In mathematics, physics, and engineering, a Euclidean vector or simply a vector (sometimes called a geometric vector or spatial vector) is a geometric object that has magnitude (or length) and direction. Vectors can be added to other vectors ...
indicating its direction and the refractive index ''n'' at point r. The optical momentum of the ray at that point is defined by
where . The geometry of the optical momentum vector is illustrated in figure "optical momentum".
In a spherical coordinate system
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the ''radial distance'' of that point from a fixed origin, its ''polar angle'' measu ...
p may be written as
from which
and therefore, for an infinitesimal area d''S'' = d''x'' d''y'' on the ''xy'' plane immersed in a medium of refractive index ''n'', the etendue is given by
which is an infinitesimal volume in phase space ''x'', ''y'', ''p'', ''q''. Conservation of etendue in phase space is the equivalent in optics to Liouville's theorem in classical mechanics. Etendue as volume in phase space is commonly used in nonimaging optics Nonimaging optics (also called anidolic optics)Roland Winston et al., ''Nonimaging Optics'', Academic Press, 2004 R. John Koshel (Editor), ''Illumination Engineering: Design with Nonimaging Optics'', Wiley, 2013 is the branch of optics concerned wi ...
.
Maximum concentration
 Consider an infinitesimal surface d''S'', immersed in a medium of refractive index ''n'' crossed by (or emitting) light inside a cone of angle ''α''. The etendue of this light is given by
Noting that ''n'' sin ''α'' is the numerical aperture ''NA'', of the beam of light, this can also be expressed as
Note that d''Ω'' is expressed in a
Consider an infinitesimal surface d''S'', immersed in a medium of refractive index ''n'' crossed by (or emitting) light inside a cone of angle ''α''. The etendue of this light is given by
Noting that ''n'' sin ''α'' is the numerical aperture ''NA'', of the beam of light, this can also be expressed as
Note that d''Ω'' is expressed in a spherical coordinate system
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the ''radial distance'' of that point from a fixed origin, its ''polar angle'' measu ...
. Now, if a large surface ''S'' is crossed by (or emits) light also confined to a cone of angle ''α'', the etendue of the light crossing ''S'' is
 The limit on maximum concentration (shown) is an optic with an entrance aperture ''S'', in air () collecting light within a solid angle of angle 2''α'' (its acceptance angle) and sending it to a smaller area receiver ''Σ'' immersed in a medium of refractive index ''n'', whose points are illuminated within a solid angle of angle 2''β''. From the above expression, the etendue of the incoming light is
and the etendue of the light reaching the receiver is
Conservation of etendue then gives
where ''C'' is the concentration of the optic. For a given angular aperture ''α'', of the incoming light, this concentration will be maximum for the maximum value of sin ''β'', that is ''β'' = π/2. The maximum possible concentration is then
In the case that the incident index is not unity, we have
and so
and in the best-case limit of ''β'' = π/2, this becomes
If the optic were a
The limit on maximum concentration (shown) is an optic with an entrance aperture ''S'', in air () collecting light within a solid angle of angle 2''α'' (its acceptance angle) and sending it to a smaller area receiver ''Σ'' immersed in a medium of refractive index ''n'', whose points are illuminated within a solid angle of angle 2''β''. From the above expression, the etendue of the incoming light is
and the etendue of the light reaching the receiver is
Conservation of etendue then gives
where ''C'' is the concentration of the optic. For a given angular aperture ''α'', of the incoming light, this concentration will be maximum for the maximum value of sin ''β'', that is ''β'' = π/2. The maximum possible concentration is then
In the case that the incident index is not unity, we have
and so
and in the best-case limit of ''β'' = π/2, this becomes
If the optic were a collimator
A collimator is a device which narrows a beam of particles or waves. To narrow can mean either to cause the directions of motion to become more aligned in a specific direction (i.e., make collimated light or parallel rays), or to cause the spati ...
instead of a concentrator, the light direction is reversed and conservation of etendue gives us the minimum aperture, ''S'', for a given output full angle 2''α''.
See also
*Light field
The light field is a vector function that describes the amount of light flowing in every direction through every point in space. The space of all possible '' light rays'' is given by the five-dimensional plenoptic function, and the magnitude of e ...
*Beam parameter product In laser science, the beam parameter product (BPP) is the product of a laser beam's divergence angle (half-angle) and the radius of the beam at its narrowest point (the beam waist). The BPP quantifies the quality of a laser beam, and how well it can ...
* Symplectic geometry
*Noether's theorem
Noether's theorem or Noether's first theorem states that every differentiable symmetry of the action of a physical system with conservative forces has a corresponding conservation law. The theorem was proven by mathematician Emmy Noether ...
*Beam emittance
In accelerator physics, emittance is a property of a charged particle beam. It refers to the area occupied by the beam in a position-and-momentum phase space.
Each particle in a beam can be described by its position and momentum along each of ...
References
Further reading
* *Xutao Sun ''et al.'', 2006, "Etendue analysis and measurement of light source with elliptical reflector", ''Displays'' (27), 56–61. * Randall Munroe explains why it's impossible to light a fire with concentrated moonlight using a etendue-conservation argument. {{cite web , last1=Munroe , first1=Randall , title=Fire from Moonlight , url=https://what-if.xkcd.com/145/ , website=What If? , accessdate=28 July 2020 Optics