Equilibrium Point

In mathematics, specifically in differential equations, an equilibrium point is a constant solution to a differential equation.

Formal definition

The point $\tilde\in \mathbb^n$ is an equilibrium point for the differential equation

:$\frac = \mathbf(t,\mathbf)$

if $\mathbf(t,\tilde)=\mathbf$ for all $t$.

Similarly, the point $\tilde\in \mathbb^n$ is an equilibrium point (or fixed point) for the difference equation

:$\mathbf_ = \mathbf(k,\mathbf_k)$

if $\mathbf(k,\tilde)= \tilde$ for $k=0,1,2,\ldots$.

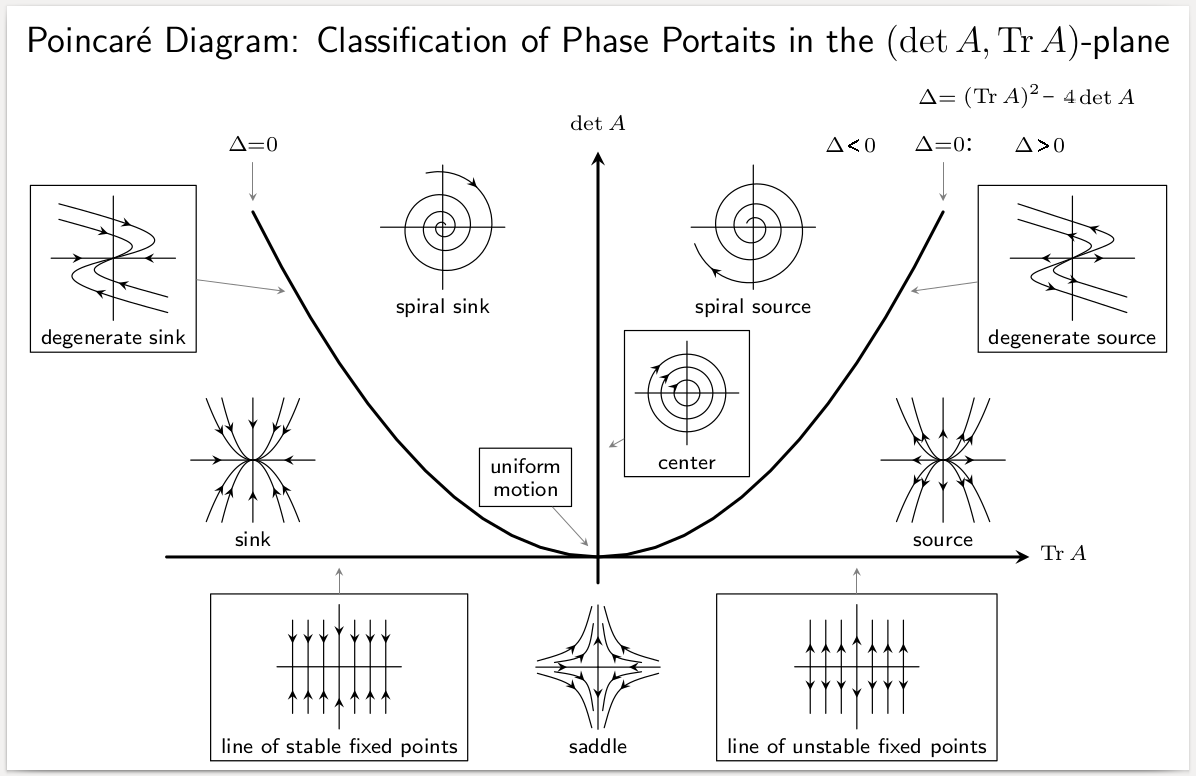
Equilibria can be classified by looking at the signs of the eigenvalues of the linearization of the equations about the equilibria. That is to say, by evaluating the Jacobian matrix at each of the equilibrium points of the system, and then finding the resulting eigenvalues, the equilibria can be categorized. Then the behavior of the system in the neighborhood of each equilibrium point can be qualitatively determined, (or even quantitatively determined, in some instances), by finding the eigenvector(s) associated with each eigenvalue.

An equilibrium point is '' hyperbolic'' if none of the eigenvalues have zero real part. If all eigenvalues have negative real parts, the point is ''stable''. If at least one has a positive real part, the point is ''unstable''. If at least one eigenvalue has negative real part and at least one has positive real part, the equilibrium is a saddle point and it is unstable. If all the eigenvalues are real and have the same sign the point is called a ''node''.

See also

* Autonomous equation
* Critical point
* Steady state

References

*
*{{cite book , last=Perko , first=Lawrence , title=Differential Equations and Dynamical Systems , publisher=Springer , edition=3rd , year=2001 , pages=102–104 , isbn=1-4613-0003-7 , url=https://books.google.com/books?id=VFnSBwAAQBAJ&pg=PA102

Stability theory
Dynamical systems