elementary cellular automaton

In mathematics and computability theory, an elementary cellular automaton is a one-dimensional cellular automaton where there are two possible states (labeled 0 and 1) and the rule to determine the state of a cell in the next generation depends only on the current state of the cell and its two immediate neighbors. There is an elementary cellular automaton (rule 110, defined below) which is capable of universal computation, and as such it is one of the simplest possible models of computation.

The numbering system

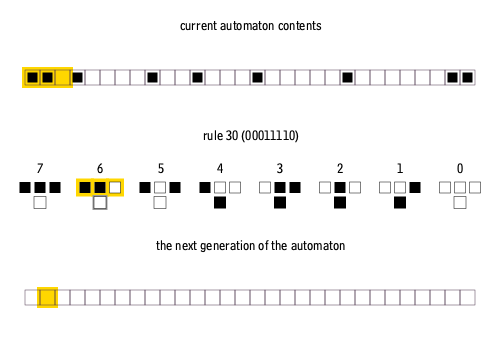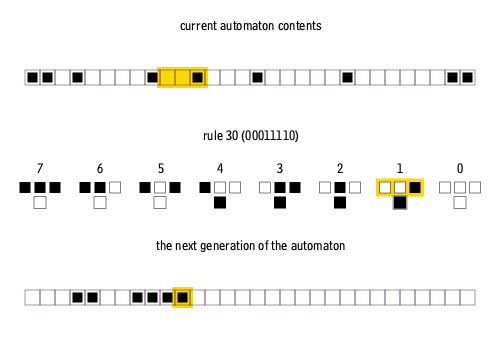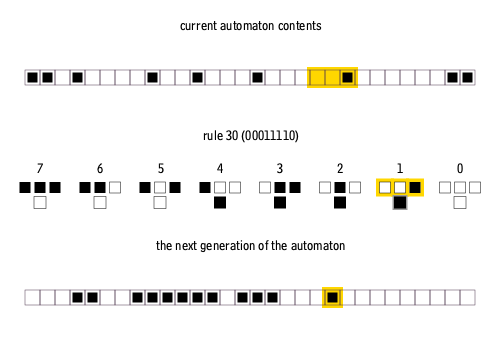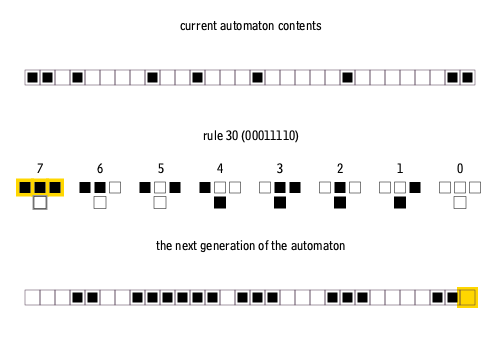
There are 8 = 2³ possible configurations for a cell and its two immediate neighbors. The rule defining the cellular automaton must specify the resulting state for each of these possibilities so there are 256 = 2²³ possible elementary cellular automata. Stephen Wolfram proposed a scheme, known as the Wolfram code, to assign each rule a number from 0 to 255 which has become standard. Each possible current configuration is written in order, 111, 110, ..., 001, 000, and the resulting state for each of these configurations is written in the same order and interpreted as the binary representation of an integer. This number is taken to be the rule number of the automaton. For example, 110_d=01101110₂. So rule 110 is defined by the transition rule:

Reflections and complements

Although there are 256 possible rules, many of these are trivially equivalent to each other up to a simple transformation of the underlying geometry. The first such transformation is reflection through a vertical axis and the result of applying this transformation to a given rule is called the mirrored rule. These rules will exhibit the same behavior up to reflection through a vertical axis, and so are equivalent in a computational sense.

For example, if the definition of rule 110 is reflected through a vertical line, the following rule (rule 124) is obtained:

Rules which are the same as their mirrored rule are called amphichiral. Of the 256 elementary cellular automata, 64 are amphichiral.

The second such transformation is to exchange the roles of 0 and 1 in the definition. The result of applying this transformation to a given rule is called the complementary rule.
For example, if this transformation is applied to rule 110, we get the following rule

and, after reordering, we discover that this is rule 137:

There are 16 rules which are the same as their complementary rules.

Finally, the previous two transformations can be applied successively to a rule to obtain the mirrored complementary rule. For example, the mirrored complementary rule of rule 110 is rule 193. There are 16 rules which are the same as their mirrored complementary rules.

Of the 256 elementary cellular automata, there are 88 which are inequivalent under these transformations.

Single 1 histories

One method used to study these automata is to follow its history with an initial state of all 0s except for a single cell with a 1. When the rule number is even (so that an input of 000 does not compute to a 1) it makes sense to interpret state at each time, ''t'', as an integer expressed in binary, producing a sequence ''a''(''t'') of integers. In many cases these sequences have simple, closed form expressions or have a generating function with a simple form. The following rules are notable:

Rule 28

The sequence generated is 1, 3, 5, 11, 21, 43, 85, 171, ... . This is the sequence of Jacobsthal numbers and has generating function

:$\frac$.

It has the closed form expression
:$a(t) = \frac$
Rule 156 generates the same sequence.

Rule 50

The sequence generated is 1, 5, 21, 85, 341, 1365, 5461, 21845, ... . This has generating function
:$\frac$.

It has the closed form expression
:$a(t) = \frac$.

Note that rules 58, 114, 122, 178, 186, 242 and 250 generate the same sequence.

Rule 54

The sequence generated is 1, 7, 17, 119, 273, 1911, 4369, 30583, ... . This has generating function
:$\frac$.

It has the closed form expression
:$a(t) = \frac$.

Rule 60

The sequence generated is 1, 3, 5, 15, 17, 51, 85, 255, .... This can be obtained by taking successive rows of Pascal's triangle modulo 2 and interpreting them as integers in binary, which can be graphically represented by a Sierpinski triangle.

Rule 90

The sequence generated is 1, 5, 17, 85, 257, 1285, 4369, 21845, ... . This can be obtained by taking successive rows of Pascal's triangle modulo 2 and interpreting them as integers in base 4. Note that rules 18, 26, 82, 146, 154, 210 and 218 generate the same sequence.

Rule 94

The sequence generated is 1, 7, 27, 119, 427, 1879, 6827, 30039, ... . This can be expressed as

:a(t) =
\begin
1, & \mboxt = 0 \\ px 7, & \mboxt = 1 \\ px \dfrac , & \mboxt\mbox \\ px \dfrac , & \mboxt\mbox
\end
.

This has generating function

:$\frac$.

Rule 102

The sequence generated is 1, 6, 20, 120, 272, 1632, 5440, 32640, ... . This is simply the sequence generated by rule 60 (which is its mirror rule) multiplied by successive powers of 2.

Rule 110

The sequence generated is 1, 6, 28, 104, 496, 1568, 7360, 27520, 130304, 396800, ... . Rule 110 has the perhaps surprising property that it is Turing complete, and thus capable of universal computation.

Rule 150

The sequence generated is 1, 7, 21, 107, 273, 1911, 5189, 28123, ... . This can be obtained by taking the coefficients of the successive powers of (1+''x''+''x''²) modulo 2 and interpreting them as integers in binary.

Rule 158

The sequence generated is 1, 7, 29, 115, 477, 1843, 7645, 29491, ... . This has generating function

:$\frac$.

Rule 188

The sequence generated is 1, 3, 5, 15, 29, 55, 93, 247, ... . This has generating function

:$\frac$.

Rule 190

The sequence generated is 1, 7, 29, 119, 477, 1911, 7645, 30583, ... . This has generating function

:$\frac$.

Rule 220

The sequence generated is 1, 3, 7, 15, 31, 63, 127, 255, ... . This is the sequence of Mersenne numbers and has generating function

:$\frac$.

It has the closed form expression
:$a(t) = 2\cdot 2^t-1$.
Note that rule 252 generates the same sequence.

Rule 222

The sequence generated is 1, 7, 31, 127, 511, 2047, 8191, 32767, ... . This is every other entry in the sequence of Mersenne numbers and has generating function

:$\frac$.

It has the closed form expression
:$a(t) = 2\cdot 4^t-1$.

Note that rule 254 generates the same sequence.

Images for rules 0-99

These images depict space-time diagrams, in which each row of pixels shows the cells of the automaton at a single point in time, with time increasing downwards. They start with an initial automaton state in which a single cell, the pixel in the center of the top row of pixels, is in state 1 and all other cells are 0.

Image:WolframRule0.png, Rule 0
Image:WolframRule1.png, Rule 1
Image:WolframRule2.png, Rule 2
Image:WolframRule3.png, Rule 3
Image:WolframRule4.png, Rule 4
Image:WolframRule5.png, Rule 5
Image:WolframRule6.png, Rule 6
Image:WolframRule7.png, Rule 7
Image:WolframRule8.png, Rule 8
Image:WolframRule9.png, Rule 9
Image:WolframRule10.png, Rule 10
Image:WolframRule11.png, Rule 11
Image:WolframRule12.png, Rule 12
Image:WolframRule13.png, Rule 13
Image:WolframRule14.png, Rule 14
Image:WolframRule15.png, Rule 15
Image:WolframRule16.png, Rule 16
Image:WolframRule17.png, Rule 17
Image:WolframRule18.png, Rule 18
Image:WolframRule19.png, Rule 19
Image:WolframRule20.png, Rule 20
Image:WolframRule21.png, Rule 21
Image:WolframRule22.png, Rule 22
Image:WolframRule23.png, Rule 23
Image:WolframRule24.png, Rule 24
Image:WolframRule25.png, Rule 25
Image:WolframRule26.png, Rule 26
Image:WolframRule27.png, Rule 27
Image:WolframRule28.png, Rule 28
Image:WolframRule29.png, Rule 29
Image:WolframRule30.png, Rule 30
Image:WolframRule31.png, Rule 31
Image:WolframRule32.png, Rule 32
Image:WolframRule33.png, Rule 33
Image:WolframRule34.png, Rule 34
Image:WolframRule35.png, Rule 35
Image:WolframRule36.png, Rule 36
Image:WolframRule37.png, Rule 37
Image:WolframRule38.png, Rule 38
Image:WolframRule39.png, Rule 39
Image:WolframRule40.png, Rule 40
Image:WolframRule41.png, Rule 41
Image:WolframRule42.png, Rule 42
Image:WolframRule43.png, Rule 43
Image:WolframRule44.png, Rule 44
Image:WolframRule45.png, Rule 45
Image:WolframRule46.png, Rule 46
Image:WolframRule47.png, Rule 47
Image:WolframRule48.png, Rule 48
Image:WolframRule49.png, Rule 49
Image:WolframRule50.png, Rule 50
Image:WolframRule51.png, Rule 51
Image:WolframRule52.png, Rule 52
Image:WolframRule53.png, Rule 53
Image:WolframRule54.png, Rule 54
Image:WolframRule55.png, Rule 55
Image:WolframRule56.png, Rule 56
Image:WolframRule57.png, Rule 57
Image:WolframRule58.png, Rule 58
Image:WolframRule59.png, Rule 59
Image:WolframRule60.png, Rule 60
Image:WolframRule61.png, Rule 61
Image:WolframRule62.png, Rule 62
Image:WolframRule63.png, Rule 63
Image:WolframRule64.png, Rule 64
Image:WolframRule65.png, Rule 65
Image:WolframRule66.png, Rule 66
Image:WolframRule67.png, Rule 67
Image:WolframRule68.png, Rule 68
Image:WolframRule69.png, Rule 69
Image:WolframRule70.png, Rule 70
Image:WolframRule71.png, Rule 71
Image:WolframRule72.png, Rule 72
Image:WolframRule73.png, Rule 73
Image:WolframRule74.png, Rule 74
Image:WolframRule75.png, Rule 75
Image:WolframRule76.png, Rule 76
Image:WolframRule77.png, Rule 77
Image:WolframRule78.png, Rule 78
Image:WolframRule79.png, Rule 79
Image:WolframRule80.png, Rule 80
Image:WolframRule81.png, Rule 81
Image:WolframRule82.png, Rule 82
Image:WolframRule83.png, Rule 83
Image:WolframRule84.png, Rule 84
Image:WolframRule85.png, Rule 85
Image:WolframRule86.png, Rule 86
Image:WolframRule87.png, Rule 87
Image:WolframRule88.png, Rule 88
Image:WolframRule89.png, Rule 89
Image:WolframRule90.png, Rule 90
Image:WolframRule91.png, Rule 91
Image:WolframRule92.png, Rule 92
Image:WolframRule93.png, Rule 93
Image:WolframRule94.png, Rule 94
Image:WolframRule95.png, Rule 95
Image:WolframRule96.png, Rule 96
Image:WolframRule97.png, Rule 97
Image:WolframRule98.png, Rule 98
Image:WolframRule99.png, Rule 99

Random initial state

A second way to investigate the behavior of these automata is to examine its history starting with a random state. This behavior can be better understood in terms of Wolfram classes. Wolfram gives the following examples as typical rules of each class.
* Class 1: Cellular automata which rapidly converge to a uniform state. Examples are rules 0, 32, 160 and 232.
* Class 2: Cellular automata which rapidly converge to a repetitive or stable state. Examples are rules 4, 108, 218 and 250.
* Class 3: Cellular automata which appear to remain in a random state. Examples are rules 22, 30, 126, 150, 182.
* Class 4: Cellular automata which form areas of repetitive or stable states, but also form structures that interact with each other in complicated ways. An example is rule 110. Rule 110 has been shown to be capable of universal computation.

Each computed result is placed under that result's source creating a two-dimensional representation of the system's evolution.

In the following gallery, this evolution from random initial conditions is shown for each of the 88 inequivalent rules. Below each image is the rule number used to produce the image, and in brackets the rule numbers of equivalent rules produced by reflection or complementing are included, if they exist.
As mentioned above, the reflected rule would produce a reflected image, while the complementary rule would produce an image with black and white swapped.

Image:Rule0rand.png, Rule 0 (255)
Image:Rule1rand.png, Rule 1 (127)
Image:Rule2rand.png, Rule 2 (16, 191, 247)
Image:Rule3rand.png, Rule 3 (17, 63, 119)
Image:Rule4rand.png, Rule 4 (223)
Image:Rule5rand.png, Rule 5 (95)
Image:Rule6rand.png, Rule 6 (20, 159, 215)
Image:Rule7rand.png, Rule 7 (21, 31, 87)
Image:Rule8rand.png, Rule 8 (64, 239, 253)
Image:Rule9rand.png, Rule 9 (65, 111, 125)
Image:Rule10rand.png, Rule 10 (80, 175, 245)
Image:Rule11rand.png, Rule 11 (47, 81, 117)
Image:Rule12rand.png, Rule 12 (68, 207, 221)
Image:Rule13rand.png, Rule 13 (69, 79, 93)
Image:Rule14rand.png, Rule 14 (84, 143, 213)
Image:Rule15rand.png, Rule 15 (85)
Image:Rule18rand.png, Rule 18 (183)
Image:Rule19rand.png, Rule 19 (55)
Image:Rule22rand.png, Rule 22 (151)
Image:Rule23rand.png, Rule 23
Image:Rule24rand.png, Rule 24 (66, 189, 231)
Image:Rule25rand.png, Rule 25 (61, 67, 103)
Image:Rule26rand.png, Rule 26 (82, 167, 181)
Image:Rule27rand.png, Rule 27 (39, 53, 83)
Image:Rule28rand.png, Rule 28 (70, 157, 199)
Image:Rule29rand.png, Rule 29 (71)
Image:Rule30rand.png, Rule 30 (86, 135, 149)
Image:Rule32rand.png, Rule 32 (251)
Image:Rule33rand.png, Rule 33 (123)
Image:Rule34rand.png, Rule 34 (48, 187, 243)
Image:Rule35rand.png, Rule 35 (49, 59, 115)
Image:Rule36rand.png, Rule 36 (219)
Image:Rule37rand.png, Rule 37 (91)
Image:Rule38rand.png, Rule 38 (52, 155, 211)
Image:Rule40rand.png, Rule 40 (96, 235, 249)
Image:Rule41rand.png, Rule 41 (97, 107, 121)
Image:Rule42rand.png, Rule 42 (112, 171, 241)
Image:Rule43rand.png, Rule 43 (113)
Image:Rule44rand.png, Rule 44 (100, 203, 217)
Image:Rule45rand.png, Rule 45 (75, 89, 101)
Image:Rule46rand.png, Rule 46 (116, 139, 209)
Image:Rule50rand.png, Rule 50 (179)
Image:Rule51rand.png, Rule 51
Image:Rule54rand.png, Rule 54 (147)
Image:Rule56rand.png, Rule 56 (98, 185, 227)
Image:Rule57rand.png, Rule 57 (99)
Image:Rule58rand.png, Rule 58 (114, 163, 177)
Image:Rule60rand.png, Rule 60 (102, 153, 195)
Image:Rule62rand.png, Rule 62 (118, 131, 145)
Image:Rule72rand.png, Rule 72 (237)
Image:Rule73rand.png, Rule 73 (109)
Image:Rule74rand.png, Rule 74 (88, 173, 229)
Image:Rule76rand.png, Rule 76 (205)
Image:Rule77rand.png, Rule 77
Image:Rule78rand.png, Rule 78 (92, 141, 197)
Image:Rule90rand.png, Rule 90 (165)
Image:Rule94rand.png, Rule 94 (133)
Image:Rule104rand.png, Rule 104 (233)
Image:Rule105rand.png, Rule 105
Image:Rule106rand.png, Rule 106 (120, 169, 225)
Image:Rule108rand.png, Rule 108 (201)
Image:Rule110rand.png, Rule 110 (124, 137, 193)
Image:Rule122rand.png, Rule 122 (161)
Image:Rule126rand.png, Rule 126 (129)
Image:Rule128rand.png, Rule 128 (254)
Image:Rule130rand.png, Rule 130 (144, 190, 246)
Image:Rule132rand.png, Rule 132 (222)
Image:Rule134rand.png, Rule 134 (148, 158, 214)
Image:Rule136rand.png, Rule 136 (192, 238, 252)
Image:Rule138rand.png, Rule 138 (174, 208, 244)
Image:Rule140rand.png, Rule 140 (196, 206, 220)
Image:Rule142rand.png, Rule 142 (212)
Image:Rule146rand.png, Rule 146 (182)
Image:Rule150rand.png, Rule 150
Image:Rule152rand.png, Rule 152 (188, 194, 230)
Image:Rule154rand.png, Rule 154 (166, 180, 210)
Image:Rule156rand.png, Rule 156 (198)
Image:Rule160rand.png, Rule 160 (250)
Image:Rule162rand.png, Rule 162 (176, 186, 242)
Image:Rule164rand.png, Rule 164 (218)
Image:Rule168rand.png, Rule 168 (224, 234, 248)
Image:Rule170rand.png, Rule 170 (240)
Image:Rule172rand.png, Rule 172 (202, 216, 228)
Image:Rule178rand.png, Rule 178
Image:Rule184rand.png, Rule 184 (226)
Image:Rule200rand.png, Rule 200 (236)
Image:Rule204rand.png, Rule 204
Image:Rule232rand.png, Rule 232

Unusual cases

In some cases the behavior of a cellular automaton is not immediately obvious. For example, for Rule 62, interacting structures develop as in a Class 4. But in these interactions at least one of the structures is annihilated so the automaton eventually enters a repetitive state and the cellular automaton is Class 2.

Rule 73 is Class 2 because any time there are two consecutive 1s surrounded by 0s, this feature is preserved in succeeding generations. This effectively creates walls which block the flow of information between different parts of the array. There are a finite number of possible configurations in the section between two walls so the automaton must eventually start repeating inside each section, though the period may be very long if the section is wide enough. These walls will form with probability 1 for completely random initial conditions. However, if the condition is added that the lengths of runs of consecutive 0s or 1s must always be odd, then the automaton displays Class 3 behavior since the walls can never form.

Rule 54 is Class 4 and also appears to be capable of universal computation, but has not been studied as thoroughly as Rule 110. Many interacting structures have been cataloged which collectively are expected to be sufficient for universality.

References

*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*

External links

{{Commons category, Elementary cellular automata

"Elementary Cellular Automata" at the ''Wolfram Atlas of Simple Programs''

32 bytes long MS-DOS executable drawing by cellular automaton
(Rule 110 by default)

A showcase of all the rules picked at randomMinimal CA emulation with Wolfram rule parser online in vanilla Javascript

Cellular automata