Elbow Method (clustering) on:
[Wikipedia]
[Google]
[Amazon]
In
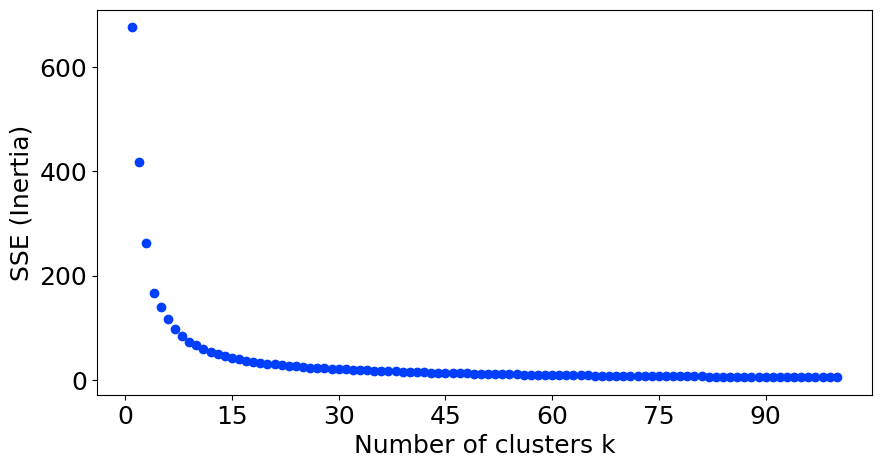 Even on uniform random data (with no meaningful clusters) the curve follows approximately the ratio ''1/k'' where ''k'' is the number of clusters parameter, causing users to see an "elbow" to mistakenly choose some "optimal" number of clusters.
Because the two axes (the number of clusters and the remaining variance) have no semantic relationship, various attempt to capture the elbow by "slope" are ill-defined and sensitive to the parameter range. Increasing the maximum number of clusters can change the location of the perceived "elbow", and in many cases alternate heuristics such as the variance-ratio-criterion or the average silhouette width are considered to be more reliable. But even with such measures, the results may depend much on the data preprocessing (feature selection and scaling) and users may come to very different clustering results on the same data.
Even on uniform random data (with no meaningful clusters) the curve follows approximately the ratio ''1/k'' where ''k'' is the number of clusters parameter, causing users to see an "elbow" to mistakenly choose some "optimal" number of clusters.
Because the two axes (the number of clusters and the remaining variance) have no semantic relationship, various attempt to capture the elbow by "slope" are ill-defined and sensitive to the parameter range. Increasing the maximum number of clusters can change the location of the perceived "elbow", and in many cases alternate heuristics such as the variance-ratio-criterion or the average silhouette width are considered to be more reliable. But even with such measures, the results may depend much on the data preprocessing (feature selection and scaling) and users may come to very different clustering results on the same data.
cluster analysis
Cluster analysis or clustering is the data analyzing technique in which task of grouping a set of objects in such a way that objects in the same group (called a cluster) are more Similarity measure, similar (in some specific sense defined by the ...
, the elbow method is a heuristic
A heuristic or heuristic technique (''problem solving'', '' mental shortcut'', ''rule of thumb'') is any approach to problem solving that employs a pragmatic method that is not fully optimized, perfected, or rationalized, but is nevertheless ...
used in determining the number of clusters in a data set. The method consists of plotting the explained variation
In statistics, explained variation measures the proportion to which a mathematical model accounts for the variation ( dispersion) of a given data set. Often, variation is quantified as variance; then, the more specific term explained variance can b ...
as a function of the number of clusters and picking the elbow of the curve as the number of clusters to use. The same method can be used to choose the number of parameters in other data-driven models, such as the number of principal component
Principal component analysis (PCA) is a linear dimensionality reduction technique with applications in exploratory data analysis, visualization and data preprocessing.
The data is linearly transformed onto a new coordinate system such that th ...
s to describe a data set.
The method can be traced to speculation by Robert L. Thorndike in 1953.
Intuition
Using the "elbow" or " knee of a curve" as a cutoff point is a common heuristic inmathematical optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criteria, from some set of available alternatives. It is generally divided into two subfiel ...
to choose a point where diminishing returns
In economics, diminishing returns means the decrease in marginal (incremental) output of a production process as the amount of a single factor of production is incrementally increased, holding all other factors of production equal ('' ceter ...
are no longer worth the additional cost. In clustering, this means one should choose a number of clusters so that adding another cluster doesn't give much better modeling of the data.
The intuition is that increasing the number of clusters will naturally improve the fit (explain more of the variation), since there are more parameters (more clusters) to use, but that at some point this is over-fitting
mathematical modeling, overfitting is "the production of an analysis that corresponds too closely or exactly to a particular set of data, and may therefore fail to fit to additional data or predict future observations reliably". An overfitt ...
, and the elbow reflects this. For example, given data that actually consist of ''k'' labeled groups – for example, ''k'' points sampled with noise – clustering with more than ''k'' clusters will "explain" more of the variation (since it can use smaller, tighter clusters), but this is over-fitting, since it is subdividing the labeled groups into multiple clusters. The idea is that the first clusters will add much information (explain a lot of variation), since the data actually consist of that many groups (so these clusters are necessary), but once the number of clusters exceeds the actual number of groups in the data, the added information will drop sharply, because it is just subdividing the actual groups. Assuming this happens, there will be a sharp elbow in the graph of explained variation versus clusters: increasing rapidly up to ''k'' ( under-fitting region), and then increasing slowly after ''k'' (over-fitting region).
Criticism
The elbow method is considered both subjective and unreliable. In many practical applications, the choice of an "elbow" is highly ambiguous as the plot does not contain a sharp elbow. This can even hold in cases where all other methods for determining the number of clusters in a data set (as mentioned in that article) agree on the number of clusters. Even on uniform random data (with no meaningful clusters) the curve follows approximately the ratio ''1/k'' where ''k'' is the number of clusters parameter, causing users to see an "elbow" to mistakenly choose some "optimal" number of clusters.
Because the two axes (the number of clusters and the remaining variance) have no semantic relationship, various attempt to capture the elbow by "slope" are ill-defined and sensitive to the parameter range. Increasing the maximum number of clusters can change the location of the perceived "elbow", and in many cases alternate heuristics such as the variance-ratio-criterion or the average silhouette width are considered to be more reliable. But even with such measures, the results may depend much on the data preprocessing (feature selection and scaling) and users may come to very different clustering results on the same data.
Even on uniform random data (with no meaningful clusters) the curve follows approximately the ratio ''1/k'' where ''k'' is the number of clusters parameter, causing users to see an "elbow" to mistakenly choose some "optimal" number of clusters.
Because the two axes (the number of clusters and the remaining variance) have no semantic relationship, various attempt to capture the elbow by "slope" are ill-defined and sensitive to the parameter range. Increasing the maximum number of clusters can change the location of the perceived "elbow", and in many cases alternate heuristics such as the variance-ratio-criterion or the average silhouette width are considered to be more reliable. But even with such measures, the results may depend much on the data preprocessing (feature selection and scaling) and users may come to very different clustering results on the same data.
Measures of variation
There are various measures of "explained variation
In statistics, explained variation measures the proportion to which a mathematical model accounts for the variation ( dispersion) of a given data set. Often, variation is quantified as variance; then, the more specific term explained variance can b ...
" used in the elbow method. Most commonly, variation is quantified by ''variance
In probability theory and statistics, variance is the expected value of the squared deviation from the mean of a random variable. The standard deviation (SD) is obtained as the square root of the variance. Variance is a measure of dispersion ...
'', and the ratio used is the ratio of between-group variance to the total variance. Alternatively, one uses the ratio of between-group variance to within-group variance, which is the one-way ANOVA
Analysis of variance (ANOVA) is a family of statistical methods used to compare the means of two or more groups by analyzing variance. Specifically, ANOVA compares the amount of variation ''between'' the group means to the amount of variation ''w ...
''F''-test statistic.See, e.g., Figure 6 in
*
See also
* Determining the number of clusters in a data set *Scree plot
In multivariate statistics, a scree plot is a line plot of the eigenvalues of factors or principal components in an analysis. The scree plot is used to determine the number of factors to retain in an exploratory factor analysis (FA) or principal c ...
References
Clustering criteria {{comp-sci-stub