Descartes' Theorem on:
[Wikipedia]
[Google]
[Amazon]
In
 Descartes' theorem is most easily stated in terms of the circles'
Descartes' theorem is most easily stated in terms of the circles'
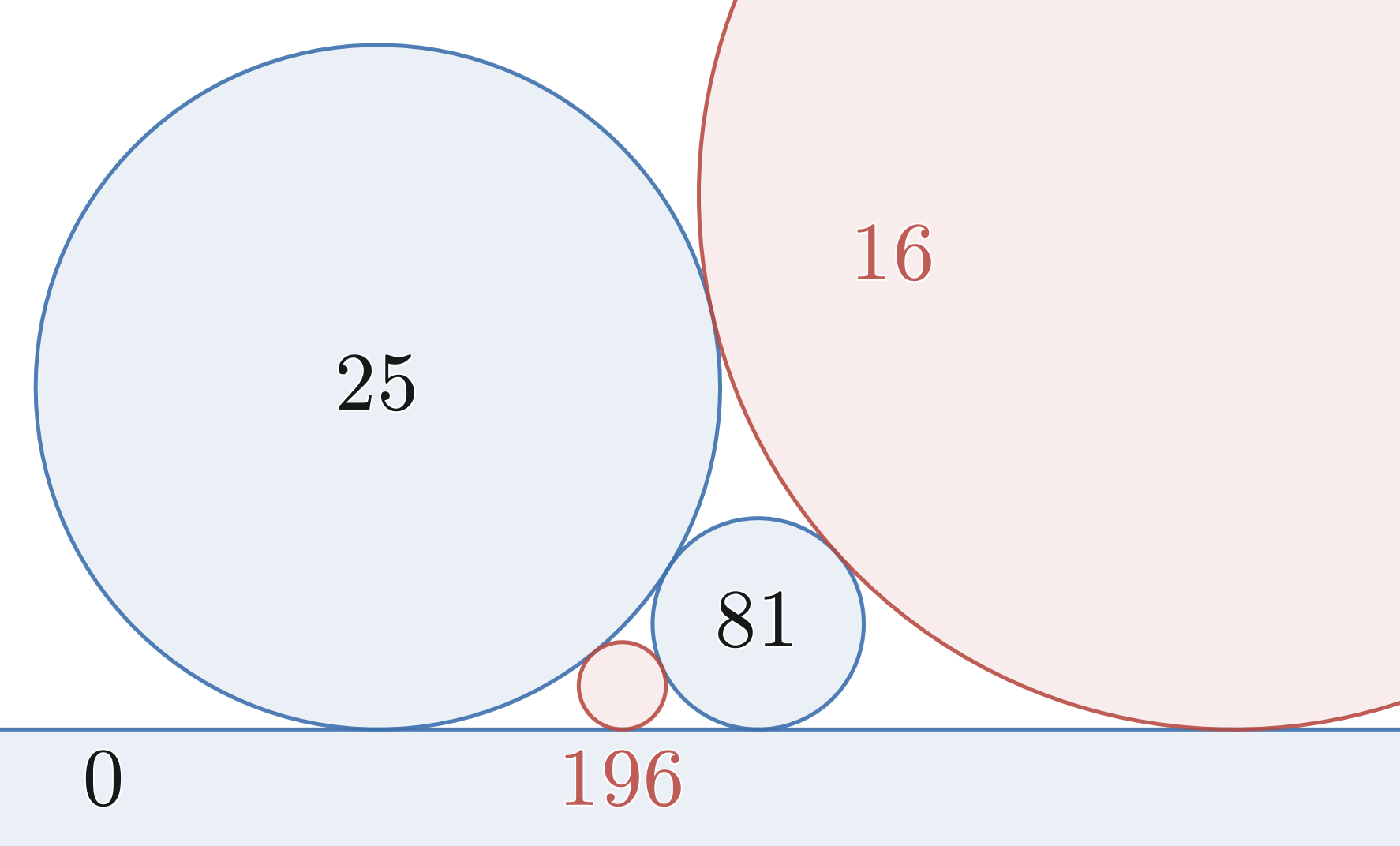
 If one of the three circles is replaced by a straight line, then one ''k''''i'', say ''k''3, is zero and drops out of . then becomes much simpler:
If two circles are replaced by lines, the tangency between the two replaced circles becomes a parallelism between their two replacement lines. For all four curves to remain mutually tangent, the other two circles must be congruent. In this case, with ''k''2 = ''k''3 = 0, is reduced to the trivial
:
It is not possible to replace three circles by lines, as it is not possible for three lines and one circle to be mutually tangent.
Descartes' theorem does not apply when all four circles are tangent to each other at the same point.
Another special case is when the ''ki'' are squares,
:
Euler showed that this is equivalent to the simultaneous triplet of
If one of the three circles is replaced by a straight line, then one ''k''''i'', say ''k''3, is zero and drops out of . then becomes much simpler:
If two circles are replaced by lines, the tangency between the two replaced circles becomes a parallelism between their two replacement lines. For all four curves to remain mutually tangent, the other two circles must be congruent. In this case, with ''k''2 = ''k''3 = 0, is reduced to the trivial
:
It is not possible to replace three circles by lines, as it is not possible for three lines and one circle to be mutually tangent.
Descartes' theorem does not apply when all four circles are tangent to each other at the same point.
Another special case is when the ''ki'' are squares,
:
Euler showed that this is equivalent to the simultaneous triplet of
Interactive applet demonstrating four mutually tangent circles
at
The Kiss Precise
{{DEFAULTSORT:Descartes' Theorem Euclidean plane geometry Theorems about circles Analytic geometry Circle packing
geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, Descartes' theorem states that for every four kissing, or mutually tangent
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More ...
, circle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is const ...
s, the radii of the circles satisfy a certain quadratic equation
In algebra, a quadratic equation () is any equation that can be rearranged in standard form as
ax^2 + bx + c = 0\,,
where represents an unknown (mathematics), unknown value, and , , and represent known numbers, where . (If and then the equati ...
. By solving this equation, one can construct a fourth circle tangent to three given, mutually tangent circles. The theorem is named after René Descartes
René Descartes ( or ; ; Latinized: Renatus Cartesius; 31 March 1596 – 11 February 1650) was a French philosopher, scientist, and mathematician, widely considered a seminal figure in the emergence of modern philosophy and science. Mathem ...
, who stated it in 1643.
History
Geometrical problems involvingtangent circles
In geometry, tangent circles (also known as kissing circles) are circles in a common plane that intersect in a single point. There are two types of tangency: internal and external. Many problems and constructions in geometry are related to tange ...
have been pondered for millennia. In ancient Greece of the third century BC, Apollonius of Perga
Apollonius of Perga ( grc-gre, Ἀπολλώνιος ὁ Περγαῖος, Apollṓnios ho Pergaîos; la, Apollonius Pergaeus; ) was an Ancient Greek geometer and astronomer known for his work on conic sections. Beginning from the contribution ...
devoted an entire book to the topic, ''De tactionibus'' 'On tangencies'' It has been lost, and is known only through mentions of it in other works.
René Descartes
René Descartes ( or ; ; Latinized: Renatus Cartesius; 31 March 1596 – 11 February 1650) was a French philosopher, scientist, and mathematician, widely considered a seminal figure in the emergence of modern philosophy and science. Mathem ...
discussed the problem briefly in 1643, in a letter to Princess Elisabeth of the Palatinate
Elisabeth of the Palatinate (26 December 1618 – 11 February 1680), also known as Elisabeth of Bohemia, Princess Elisabeth of the Palatinate, or Princess-Abbess of Herford Abbey, was the eldest daughter of Frederick V, Elector Palatine (who was ...
. He came up with the equation describing the relation between the radii, or curvatures, of four pairwise tangent circles. This result became known as Descartes' theorem.
This result was rediscovered in 1826 by Jakob Steiner
Jakob Steiner (18 March 1796 – 1 April 1863) was a Swiss mathematician who worked primarily in geometry.
Life
Steiner was born in the village of Utzenstorf, Canton of Bern. At 18, he became a pupil of Heinrich Pestalozzi and afterwards st ...
, in 1842 by Philip Beecroft, and in 1936 by Frederick Soddy
Frederick Soddy FRS (2 September 1877 – 22 September 1956) was an English radiochemist who explained, with Ernest Rutherford, that radioactivity is due to the transmutation of elements, now known to involve nuclear reactions. He also prov ...
. The kissing circles in this problem are sometimes known as Soddy circles and line connecting their centers as Soddy line perhaps because Soddy chose to publish his version of the theorem in the form of a poem, titled ''The Kiss Precise''. Soddy also extended the theorem to spheres; Thorold Gosset
John Herbert de Paz Thorold Gosset (16 October 1869 – December 1962) was an English lawyer and an amateur mathematician. In mathematics, he is noted for discovering and classifying the semiregular polytopes in dimensions four and higher, and ...
extended the theorem to arbitrary dimensions.
Definition of curvature
curvature
In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane.
For curves, the canonic ...
s. The curvature (or bend) of a circle is defined as , where is its radius. The larger a circle, the smaller is the magnitude
Magnitude may refer to:
Mathematics
*Euclidean vector, a quantity defined by both its magnitude and its direction
*Magnitude (mathematics), the relative size of an object
*Norm (mathematics), a term for the size or length of a vector
*Order of ...
of its curvature, and vice versa.
The sign in (represented by the symbol) is positive for a circle that is ''externally'' tangent to the other circles, like the three black circles in the image. For an ''internally'' tangent circle like the large red circle, that ''circumscribes'' the other circles, the sign is negative. If a straight line is considered a degenerate
Degeneracy, degenerate, or degeneration may refer to:
Arts and entertainment
* Degenerate (album), ''Degenerate'' (album), a 2010 album by the British band Trigger the Bloodshed
* Degenerate art, a term adopted in the 1920s by the Nazi Party i ...
circle with zero curvature (and thus infinite radius), Descartes' theorem also applies to a line and three circles that are all three mutually tangent.
For four circles that are tangent to each other at six distinct points, with curvatures for , Descartes' theorem says:
When trying to find the radius of a fourth circle tangent to three given kissing circles, the equation is best rewritten as:
The ± sign reflects the fact that there are in general ''two'' solutions to this equation, and two tangent circles (or degenerate straight lines) to any triple of tangent circles. Problem-specific criteria may favor one of these two solutions over the other in any given problem.
Special cases

 If one of the three circles is replaced by a straight line, then one ''k''''i'', say ''k''3, is zero and drops out of . then becomes much simpler:
If two circles are replaced by lines, the tangency between the two replaced circles becomes a parallelism between their two replacement lines. For all four curves to remain mutually tangent, the other two circles must be congruent. In this case, with ''k''2 = ''k''3 = 0, is reduced to the trivial
:
It is not possible to replace three circles by lines, as it is not possible for three lines and one circle to be mutually tangent.
Descartes' theorem does not apply when all four circles are tangent to each other at the same point.
Another special case is when the ''ki'' are squares,
:
Euler showed that this is equivalent to the simultaneous triplet of
If one of the three circles is replaced by a straight line, then one ''k''''i'', say ''k''3, is zero and drops out of . then becomes much simpler:
If two circles are replaced by lines, the tangency between the two replaced circles becomes a parallelism between their two replacement lines. For all four curves to remain mutually tangent, the other two circles must be congruent. In this case, with ''k''2 = ''k''3 = 0, is reduced to the trivial
:
It is not possible to replace three circles by lines, as it is not possible for three lines and one circle to be mutually tangent.
Descartes' theorem does not apply when all four circles are tangent to each other at the same point.
Another special case is when the ''ki'' are squares,
:
Euler showed that this is equivalent to the simultaneous triplet of Pythagorean triple
A Pythagorean triple consists of three positive integers , , and , such that . Such a triple is commonly written , and a well-known example is . If is a Pythagorean triple, then so is for any positive integer . A primitive Pythagorean triple is ...
s,
:
:
:
and can be given a parametric solution
In mathematics, a parametric equation defines a group of quantities as functions of one or more independent variables called parameters. Parametric equations are commonly used to express the coordinates of the points that make up a geometric obj ...
. When the minus sign of a curvature is chosen,
:
this can be solved as,
:
where
:
parametric solutions of which are well-known.
Complex Descartes theorem
To determine a circle completely, not only its radius (or curvature), but also its center must be known. The relevant equation is expressed most clearly if the coordinates (''x'', ''y'') are interpreted as acomplex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form ...
''z'' = ''x'' + i''y''. The equation then looks similar to Descartes' theorem and is therefore called the complex Descartes theorem.
Given four circles with curvatures ''k''''i'' and centers ''z''''i'' (for ''i'' = 1...4), the following equality holds in addition to :
Once ''k''4 has been found using , one may proceed to calculate ''z''4 by rewriting to a form similar to :
:
Again, in general, there are two solutions for ''z''4, corresponding to the two solutions for ''k''4. Note that the plus/minus sign in the above formula for z does not necessarily correspond to the plus/minus sign in the formula for k.
Generalizations
The generalization to n dimensions is sometimes referred to as the Soddy–Gosset theorem, even though it was shown by R. Lachlan in 1886. In -dimensionalEuclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's Elements, Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics ther ...
, the maximum number of mutually tangent -spheres is . For example, in 3-dimensional space, five spheres can be mutually tangent. The curvatures of the hyperspheres satisfy
:
with the case corresponding to a flat hyperplane, in exact analogy to the 2-dimensional version of the theorem.
Although there is no 3-dimensional analogue of the complex numbers, the relationship between the positions of the centers can be re-expressed as a matrix
Matrix most commonly refers to:
* ''The Matrix'' (franchise), an American media franchise
** ''The Matrix'', a 1999 science-fiction action film
** "The Matrix", a fictional setting, a virtual reality environment, within ''The Matrix'' (franchis ...
equation, which also generalizes to dimensions.
See also
*Ford circle
In mathematics, a Ford circle is a circle with center at (p/q,1/(2q^2)) and radius 1/(2q^2), where p/q is an irreducible fraction, i.e. p and q are coprime integers. Each Ford circle is tangent to the horizontal axis y=0, and any two Ford circles ...
s
* Apollonian gasket
In mathematics, an Apollonian gasket or Apollonian net is a fractal generated by starting with a triple of circles, each tangent to the other two, and successively filling in more circles, each tangent to another three. It is named after Greek mat ...
* Problem of Apollonius ("circle tangencies")
* Soddy's hexlet
In geometry, Soddy's hexlet is a chain of six spheres (shown in grey in Figure 1), each of which is tangent to both of its neighbors and also to three mutually tangent given spheres. In Figure 1, the three spheres are the red inner sphere and tw ...
* Tangent lines to circles
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More ...
* Isoperimetric point
In geometry, the isoperimetric point is a special point associated with a plane triangle. The term was originally introduced by G.R. Veldkamp in a paper published in the American Mathematical Monthly in 1985 to denote a point ''P'' in the plane of ...
Notes
External links
Interactive applet demonstrating four mutually tangent circles
at
cut-the-knot
Alexander Bogomolny (January 4, 1948 July 7, 2018) was a Soviet-born Israeli-American mathematician. He was Professor Emeritus of Mathematics at the University of Iowa, and formerly research fellow at the Moscow Institute of Electronics and Math ...
The Kiss Precise
{{DEFAULTSORT:Descartes' Theorem Euclidean plane geometry Theorems about circles Analytic geometry Circle packing