Double Pendulum on:
[Wikipedia]
[Google]
[Amazon]
In
 The double pendulum undergoes chaotic motion, and shows a sensitive dependence on
The double pendulum undergoes chaotic motion, and shows a sensitive dependence on 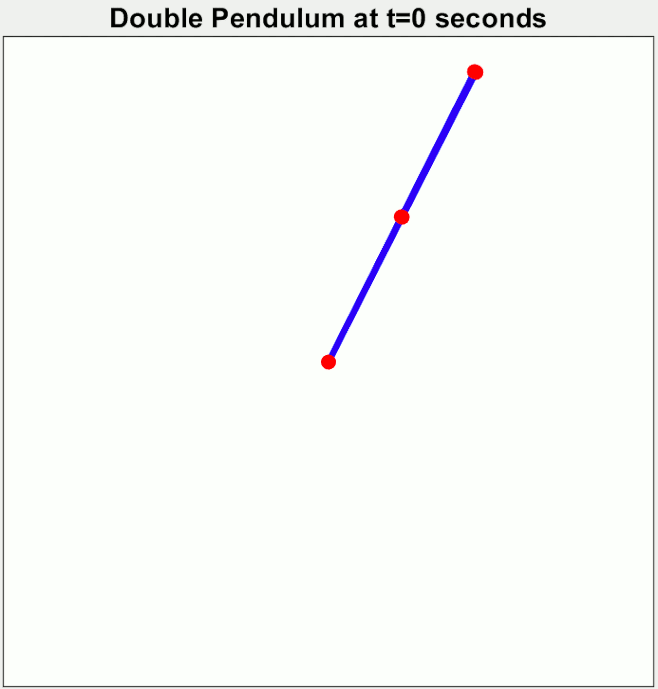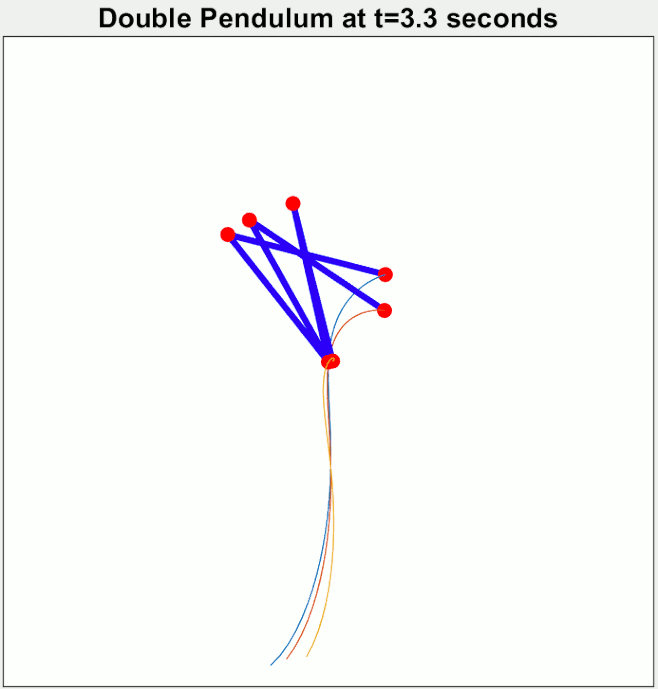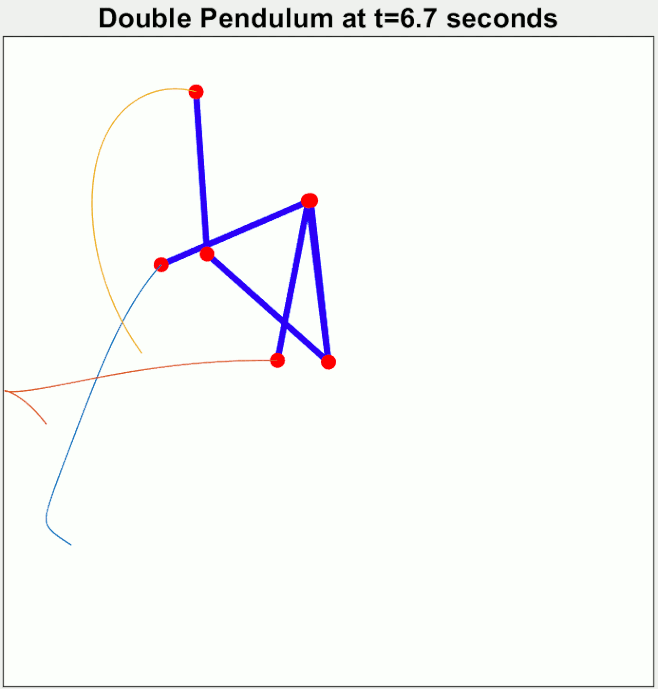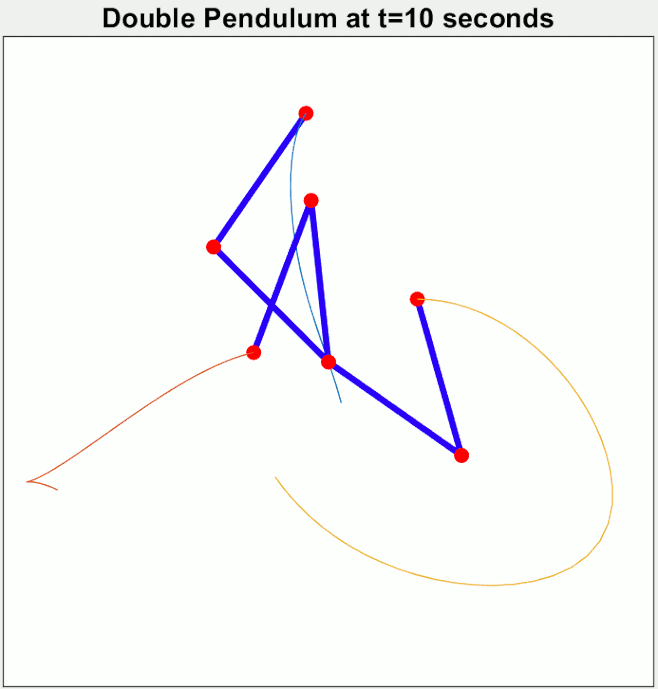 Initial conditions that do not lead to a flip within are plotted white.
The boundary of the central white region is defined in part by energy conservation with the following curve:
:
Within the region defined by this curve, that is if
:
then it is energetically impossible for either pendulum to flip. Outside this region, the pendulum can flip, but it is a complex question to determine when it will flip. Similar behavior is observed for a double pendulum composed of two
Initial conditions that do not lead to a flip within are plotted white.
The boundary of the central white region is defined in part by energy conservation with the following curve:
:
Within the region defined by this curve, that is if
:
then it is energetically impossible for either pendulum to flip. Outside this region, the pendulum can flip, but it is a complex question to determine when it will flip. Similar behavior is observed for a double pendulum composed of two
Sample Final Project: One Signature of Chaos in the Double Pendulum
', (2013). A report produced as an example for students. Includes a derivation of the equations of motion, and a comparison between the double pendulum with 2 point masses and the double pendulum with 2 rods. The lack of a natural excitation frequency has led to the use of double pendulum systems in seismic resistance designs in buildings, where the building itself is the primary inverted pendulum, and a secondary mass is connected to complete the double pendulum.
Double pendulum
' (2005), ScienceWorld ''(contains details of the complicated equations involved)'' and
Double Pendulum
by Rob Morris,
Double Pendulum
', (2001). ''(Java applet simulation.)'' * Northwestern University,
'', ''(Java applet simulation.)'' * Theoretical High-Energy Astrophysics Group at UBC,
Double pendulum
', (2005).
double pendulum
and
physical double pendulum (two square plates)
by Mike Wheatland (Univ. Sydney) *Interactive Open Source Physics JavaScript simulation with detailed equation
double pendulum
*Interactive Javascript simulation of
*Double pendulum physics simulation fro
usin
open source JavaScript code
*Simulation, equations and explanation o
Rott's pendulum
*
Double Pendulum Simulator
- An open source simulator written in
Online Java simulator
of the Imaginary exhibition. {{Chaos theory Chaotic maps Dynamical systems Mathematical physics Pendulums
physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which r ...
and mathematics, in the area of dynamical systems, a double pendulum also known as a chaos pendulum is a pendulum
A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward th ...
with another pendulum attached to its end, forming a simple physical system that exhibits rich dynamic behavior with a strong sensitivity to initial conditions. The motion of a double pendulum is governed by a set of coupled ordinary differential equation
In mathematics, an ordinary differential equation (ODE) is a differential equation whose unknown(s) consists of one (or more) function(s) of one variable and involves the derivatives of those functions. The term ''ordinary'' is used in contrast ...
s and is chaotic
Chaotic was originally a Danish trading card game. It expanded to an online game in America which then became a television program based on the game. The program was able to be seen on 4Kids TV (Fox affiliates, nationwide), Jetix, The CW4Kid ...
.
Analysis and interpretation
Several variants of the double pendulum may be considered; the two limbs may be of equal or unequal lengths and masses, they may besimple pendulum
A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward th ...
s or compound pendulum
A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward th ...
s (also called complex pendulums) and the motion may be in three dimensions or restricted to the vertical plane. In the following analysis, the limbs are taken to be identical compound pendulums of length and mass , and the motion is restricted to two dimensions.
In a compound pendulum, the mass is distributed along its length. If the mass is evenly distributed, then the center of mass of each limb is at its midpoint, and the limb has a moment of inertia of about that point.
It is convenient to use the angles between each limb and the vertical as the generalized coordinates
In analytical mechanics, generalized coordinates are a set of parameters used to represent the state of a system in a configuration space. These parameters must uniquely define the configuration of the system relative to a reference state.,p. 39 ...
defining the configuration of the system. These angles are denoted and . The position of the center of mass of each rod may be written in terms of these two coordinates. If the origin of the Cartesian coordinate system is taken to be at the point of suspension of the first pendulum, then the center of mass of this pendulum is at:
:
and the center of mass of the second pendulum is at
:
This is enough information to write out the Lagrangian.
Lagrangian
TheLagrangian
Lagrangian may refer to:
Mathematics
* Lagrangian function, used to solve constrained minimization problems in optimization theory; see Lagrange multiplier
** Lagrangian relaxation, the method of approximating a difficult constrained problem with ...
is
:
The first term is the ''linear'' kinetic energy
In physics, the kinetic energy of an object is the energy that it possesses due to its motion.
It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acc ...
of the center of mass of the bodies and the second term is the ''rotational'' kinetic energy around the center of mass of each rod. The last term is the potential energy of the bodies in a uniform gravitational field. The dot-notation indicates the time derivative
A time derivative is a derivative of a function with respect to time, usually interpreted as the rate of change of the value of the function. The variable denoting time is usually written as t.
Notation
A variety of notations are used to denote th ...
of the variable in question.
Substituting the coordinates above and rearranging the equation gives
:
There is only one conserved quantity (the energy), and no conserved momenta. The two generalized momenta may be written as
:
These expressions may be inverted to get
:
The remaining equations of motion are written as
:
These last four equations are explicit formulas for the time evolution of the system given its current state. It is not possible to go further and integrate these equations to an expression in closed form, to get formulas for and as functions of time. It is, however, possible to perform this integration numerically using the Runge Kutta Runge may refer to:
Locations
* Runge, Texas, a town, United States
*Runge (crater), a lunar crater Mare Smythii
Other uses
*Runge Newspapers, a newspaper chain in Ontario, Canada
*Inspector Heinrich Runge (though it is more often spelled ...
method or similar techniques.
Chaotic motion
 The double pendulum undergoes chaotic motion, and shows a sensitive dependence on
The double pendulum undergoes chaotic motion, and shows a sensitive dependence on initial conditions
In mathematics and particularly in dynamic systems, an initial condition, in some contexts called a seed value, is a value of an evolving variable at some point in time designated as the initial time (typically denoted ''t'' = 0). For ...
. The image to the right shows the amount of elapsed time before the pendulum flips over, as a function of initial position when released at rest. Here, the initial value of ranges along the -direction from −3.14 to 3.14. The initial value ranges along the -direction, from −3.14 to 3.14. The colour of each pixel indicates whether either pendulum flips within:
* (black)
* (red)
* (green)
* (blue) or
* (purple).
 Initial conditions that do not lead to a flip within are plotted white.
The boundary of the central white region is defined in part by energy conservation with the following curve:
:
Within the region defined by this curve, that is if
:
then it is energetically impossible for either pendulum to flip. Outside this region, the pendulum can flip, but it is a complex question to determine when it will flip. Similar behavior is observed for a double pendulum composed of two
Initial conditions that do not lead to a flip within are plotted white.
The boundary of the central white region is defined in part by energy conservation with the following curve:
:
Within the region defined by this curve, that is if
:
then it is energetically impossible for either pendulum to flip. Outside this region, the pendulum can flip, but it is a complex question to determine when it will flip. Similar behavior is observed for a double pendulum composed of two point mass
A point particle (ideal particle or point-like particle, often spelled pointlike particle) is an idealization of particles heavily used in physics. Its defining feature is that it lacks spatial extension; being dimensionless, it does not take up ...
es rather than two rods with distributed mass.Alex Small, Sample Final Project: One Signature of Chaos in the Double Pendulum
', (2013). A report produced as an example for students. Includes a derivation of the equations of motion, and a comparison between the double pendulum with 2 point masses and the double pendulum with 2 rods. The lack of a natural excitation frequency has led to the use of double pendulum systems in seismic resistance designs in buildings, where the building itself is the primary inverted pendulum, and a secondary mass is connected to complete the double pendulum.
See also
*Double inverted pendulum
A double inverted pendulum is the combination of the inverted pendulum and the double pendulum. The double inverted pendulum is unstable, meaning that it will fall down unless it is controlled in some way. The two main methods of controlling a dou ...
* Pendulum (mechanics)
* Mid-20th century physics textbooks use the term "double pendulum" to mean a single bob suspended from a string which is in turn suspended from a V-shaped string. This type of pendulum
A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward th ...
, which produces Lissajous curves, is now referred to as a Blackburn pendulum.
Notes
References
* * Eric W. Weisstein,Double pendulum
' (2005), ScienceWorld ''(contains details of the complicated equations involved)'' and
Double Pendulum
by Rob Morris,
Wolfram Demonstrations Project
The Wolfram Demonstrations Project is an organized, open-source collection of small (or medium-size) interactive programs called Demonstrations, which are meant to visually and interactively represent ideas from a range of fields. It is hos ...
, 2007 (animations of those equations).
* Peter Lynch
Peter Lynch (born January 19, 1944) is an American investor, mutual fund manager, and philanthropist. As the manager of the Magellan Fund at Fidelity Investments between 1977 and 1990, Lynch averaged a 29.2% annual return, consistently more th ...
, Double Pendulum
', (2001). ''(Java applet simulation.)'' * Northwestern University,
'', ''(Java applet simulation.)'' * Theoretical High-Energy Astrophysics Group at UBC,
Double pendulum
', (2005).
External links
*Animations and explanations ofdouble pendulum
and
physical double pendulum (two square plates)
by Mike Wheatland (Univ. Sydney) *Interactive Open Source Physics JavaScript simulation with detailed equation
double pendulum
*Interactive Javascript simulation of
*Double pendulum physics simulation fro
usin
open source JavaScript code
*Simulation, equations and explanation o
Rott's pendulum
*
Double Pendulum Simulator
- An open source simulator written in
C++
C++ (pronounced "C plus plus") is a high-level general-purpose programming language created by Danish computer scientist Bjarne Stroustrup as an extension of the C programming language, or "C with Classes". The language has expanded significan ...
using the Qt toolkit
Qt (pronounced "cute") is cross-platform software for creating graphical user interfaces as well as cross-platform applications that run on various software and hardware platforms such as Linux, Windows, macOS, Android or embedded systems wi ...
.
Online Java simulator
of the Imaginary exhibition. {{Chaos theory Chaotic maps Dynamical systems Mathematical physics Pendulums