divisor class group on:
[Wikipedia]
[Google]
[Amazon]
In
 Let ''X'' be the
Let ''X'' be the
algebraic geometry
Algebraic geometry is a branch of mathematics which uses abstract algebraic techniques, mainly from commutative algebra, to solve geometry, geometrical problems. Classically, it studies zero of a function, zeros of multivariate polynomials; th ...
, divisors are a generalization of codimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, to submanifolds in manifolds, and suitable subsets of algebraic varieties.
For affine and projective algebraic varieties, the codimension equals ...
-1 subvarieties of algebraic varieties
Algebraic varieties are the central objects of study in algebraic geometry, a sub-field of mathematics. Classically, an algebraic variety is defined as the set of solutions of a system of polynomial equations over the real or complex numbers. ...
. Two different generalizations are in common use, Cartier divisors and Weil divisors (named for Pierre Cartier and André Weil
André Weil (; ; 6 May 1906 – 6 August 1998) was a French mathematician, known for his foundational work in number theory and algebraic geometry. He was one of the most influential mathematicians of the twentieth century. His influence is du ...
by David Mumford). Both are derived from the notion of divisibility in the integer
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative in ...
s and algebraic number field
In mathematics, an algebraic number field (or simply number field) is an extension field K of the field of rational numbers such that the field extension K / \mathbb has finite degree (and hence is an algebraic field extension).
Thus K is a ...
s.
Globally, every codimension-1 subvariety of projective space
In mathematics, the concept of a projective space originated from the visual effect of perspective, where parallel lines seem to meet ''at infinity''. A projective space may thus be viewed as the extension of a Euclidean space, or, more generally ...
is defined by the vanishing of one homogeneous polynomial; by contrast, a codimension-''r'' subvariety need not be definable by only ''r'' equations when ''r'' is greater than 1. (That is, not every subvariety of projective space is a complete intersection
In mathematics, an algebraic variety ''V'' in projective space is a complete intersection if the ideal of ''V'' is generated by exactly ''codim V'' elements. That is, if ''V'' has dimension ''m'' and lies in projective space ''P'n'', there s ...
.) Locally, every codimension-1 subvariety of a smooth variety In algebraic geometry, a smooth scheme over a Field (mathematics), field is a scheme (mathematics), scheme which is well approximated by affine space near any point. Smoothness is one way of making precise the notion of a scheme with no Singular poi ...
can be defined by one equation in a neighborhood of each point. Again, the analogous statement fails for higher-codimension subvarieties. As a result of this property, much of algebraic geometry studies an arbitrary variety by analysing its codimension-1 subvarieties and the corresponding line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example, a curve in the plane having a tangent line at each point determines a varying line: the ''tangent bundle'' is a way of organis ...
s.
On singular varieties, this property can also fail, and so one has to distinguish between codimension-1 subvarieties and varieties which can locally be defined by one equation. The former are Weil divisors while the latter are Cartier divisors.
Topologically, Weil divisors play the role of homology classes, while Cartier divisors represent cohomology
In mathematics, specifically in homology theory and algebraic topology, cohomology is a general term for a sequence of abelian groups, usually one associated with a topological space, often defined from a cochain complex. Cohomology can be viewed ...
classes. On a smooth variety (or more generally a regular scheme), a result analogous to Poincaré duality
In mathematics, the Poincaré duality theorem, named after Henri Poincaré, is a basic result on the structure of the homology (mathematics), homology and cohomology group (mathematics), groups of manifolds. It states that if ''M'' is an ''n''-dim ...
says that Weil and Cartier divisors are the same.
The name "divisor" goes back to the work of Dedekind and Weber, who showed the relevance of Dedekind domain
In mathematics, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily un ...
s to the study of algebraic curve
In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane cu ...
s. The group of divisors on a curve (the free abelian group generated by all divisors) is closely related to the group of fractional ideal
In mathematics, in particular commutative algebra, the concept of fractional ideal is introduced in the context of integral domains and is particularly fruitful in the study of Dedekind domains. In some sense, fractional ideals of an integral do ...
s for a Dedekind domain.
An algebraic cycle is a higher codimension generalization of a divisor; by definition, a Weil divisor is a cycle of codimension 1.
Divisors on a Riemann surface
ARiemann surface
In mathematics, particularly in complex analysis, a Riemann surface is a connected one-dimensional complex manifold. These surfaces were first studied by and are named after Bernhard Riemann. Riemann surfaces can be thought of as deformed vers ...
is a 1-dimensional complex manifold
In differential geometry and complex geometry, a complex manifold is a manifold with a ''complex structure'', that is an atlas (topology), atlas of chart (topology), charts to the open unit disc in the complex coordinate space \mathbb^n, such th ...
, and so its codimension-1 submanifolds have dimension 0. The group of divisors on a compact
Compact as used in politics may refer broadly to a pact or treaty; in more specific cases it may refer to:
* Interstate compact, a type of agreement used by U.S. states
* Blood compact, an ancient ritual of the Philippines
* Compact government, a t ...
Riemann surface ''X'' is the free abelian group on the points of ''X''.
Equivalently, a divisor on a compact Riemann surface ''X'' is a finite linear combination
In mathematics, a linear combination or superposition is an Expression (mathematics), expression constructed from a Set (mathematics), set of terms by multiplying each term by a constant and adding the results (e.g. a linear combination of ''x'' a ...
of points of ''X'' with integer
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative in ...
coefficients. The degree of a divisor on ''X'' is the sum of its coefficients.
For any nonzero meromorphic function
In the mathematical field of complex analysis, a meromorphic function on an open subset ''D'' of the complex plane is a function that is holomorphic on all of ''D'' ''except'' for a set of isolated points, which are ''poles'' of the function. ...
''f'' on ''X'', one can define the order of vanishing of ''f'' at a point ''p'' in ''X'', ord''p''(''f''). It is an integer, negative if ''f'' has a pole at ''p''. The divisor of a nonzero meromorphic function ''f'' on the compact Riemann surface ''X'' is defined as
:
which is a finite sum. Divisors of the form (''f'') are also called principal divisors. Since (''fg'') = (''f'') + (''g''), the set of principal divisors is a subgroup of the group of divisors. Two divisors that differ by a principal divisor are called linearly equivalent.
On a compact Riemann surface, the degree of a principal divisor is zero; that is, the number of zeros of a meromorphic function is equal to the number of poles, counted with multiplicity. As a result, the degree is well-defined on linear equivalence classes of divisors.
Given a divisor ''D'' on a compact Riemann surface ''X'', it is important to study the complex vector space
In mathematics and physics, a vector space (also called a linear space) is a set (mathematics), set whose elements, often called vector (mathematics and physics), ''vectors'', can be added together and multiplied ("scaled") by numbers called sc ...
of meromorphic functions on ''X'' with poles at most given by ''D'', called ''H''0(''X'', ''O''(''D'')) or the space of sections of the line bundle associated to ''D''. The degree of ''D'' says a lot about the dimension of this vector space. For example, if ''D'' has negative degree, then this vector space is zero (because a meromorphic function cannot have more zeros than poles). If ''D'' has positive degree, then the dimension of ''H''0(''X'', ''O''(''mD'')) grows linearly in ''m'' for ''m'' sufficiently large. The Riemann–Roch theorem
The Riemann–Roch theorem is an important theorem in mathematics, specifically in complex analysis and algebraic geometry, for the computation of the dimension of the space of meromorphic functions with prescribed zeros and allowed poles. It re ...
is a more precise statement along these lines. On the other hand, the precise dimension of ''H''0(''X'', ''O''(''D'')) for divisors ''D'' of low degree is subtle, and not completely determined by the degree of ''D''. The distinctive features of a compact Riemann surface are reflected in these dimensions.
One key divisor on a compact Riemann surface is the canonical divisor
The adjective canonical is applied in many contexts to mean 'according to the canon' the standard, rule or primary source that is accepted as authoritative for the body of knowledge or literature in that context. In mathematics, ''canonical examp ...
. To define it, one first defines the divisor of a nonzero meromorphic 1-form
In differential geometry, a one-form (or covector field) on a differentiable manifold is a differential form of degree one, that is, a smooth section of the cotangent bundle. Equivalently, a one-form on a manifold M is a smooth mapping of the t ...
along the lines above. Since the space of meromorphic 1-forms is a 1-dimensional vector space over the field of meromorphic functions, any two nonzero meromorphic 1-forms yield linearly equivalent divisors. Any divisor in this linear equivalence class is called the canonical divisor of ''X'', ''K''''X''. The genus
Genus (; : genera ) is a taxonomic rank above species and below family (taxonomy), family as used in the biological classification of extant taxon, living and fossil organisms as well as Virus classification#ICTV classification, viruses. In bino ...
''g'' of ''X'' can be read from the canonical divisor: namely, ''K''''X'' has degree 2''g'' − 2. The key trichotomy among compact Riemann surfaces ''X'' is whether the canonical divisor has negative degree (so ''X'' has genus zero), zero degree (genus one), or positive degree (genus at least 2). For example, this determines whether ''X'' has a Kähler metric with positive curvature
In mathematics, curvature is any of several strongly related concepts in geometry that intuitively measure the amount by which a curve deviates from being a straight line or by which a surface deviates from being a plane. If a curve or su ...
, zero curvature, or negative curvature. The canonical divisor has negative degree if and only if ''X'' is isomorphic to the Riemann sphere
In mathematics, the Riemann sphere, named after Bernhard Riemann,
is a Mathematical model, model of the extended complex plane (also called the closed complex plane): the complex plane plus one point at infinity. This extended plane represents ...
CP1.
Weil divisors
Let ''X'' be anintegral
In mathematics, an integral is the continuous analog of a Summation, sum, which is used to calculate area, areas, volume, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental oper ...
locally Noetherian scheme. A prime divisor or irreducible divisor on ''X'' is an integral closed subscheme ''Z'' of codimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, to submanifolds in manifolds, and suitable subsets of algebraic varieties.
For affine and projective algebraic varieties, the codimension equals ...
1 in ''X''. A Weil divisor on ''X'' is a formal sum over the prime divisors ''Z'' of ''X'',
:
where the collection is locally finite. If ''X'' is quasi-compact (i.e., Noetherian), local finiteness is equivalent to being finite. The group of all Weil divisors is denoted . A Weil divisor ''D'' is effective if all the coefficients are non-negative. One writes if the difference is effective.
For example, a divisor on an algebraic curve over a field is a formal sum of finitely many closed points. A divisor on is a formal sum of prime numbers with integer coefficients and therefore corresponds to a non-zero fractional ideal in Q. A similar characterization is true for divisors on where ''K'' is a number field.
If ''Z'' ⊂ ''X'' is a prime divisor, then the local ring has Krull dimension
In commutative algebra, the Krull dimension of a commutative ring ''R'', named after Wolfgang Krull, is the supremum of the lengths of all chains of prime ideals. The Krull dimension need not be finite even for a Noetherian ring. More generally ...
one. If is non-zero, then the order of vanishing of ''f'' along ''Z'', written , is the length
Length is a measure of distance. In the International System of Quantities, length is a quantity with Dimension (physical quantity), dimension distance. In most systems of measurement a Base unit (measurement), base unit for length is chosen, ...
of This length is finite, and it is additive with respect to multiplication, that is, . If ''k''(''X'') is the field of rational functions on ''X'', then any non-zero may be written as a quotient , where ''g'' and ''h'' are in and the order of vanishing of ''f'' is defined to be . With this definition, the order of vanishing is a function . If ''X'' is normal, then the local ring is a discrete valuation ring, and the function is the corresponding valuation. For a non-zero rational function ''f'' on ''X'', the principal Weil divisor associated to ''f'' is defined to be the Weil divisor
:
It can be shown that this sum is locally finite and hence that it indeed defines a Weil divisor. The principal Weil divisor associated to ''f'' is also notated . If ''f'' is a regular function, then its principal Weil divisor is effective, but in general this is not true. The additivity of the order of vanishing function implies that
:
Consequently is a homomorphism, and in particular its image is a subgroup of the group of all Weil divisors.
Let ''X'' be a normal integral Noetherian scheme. Every Weil divisor ''D'' determines a coherent sheaf
In mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaves are a class of sheaves closely linked to the geometric properties of the underlying space. The definition of coherent sheaves is made with refer ...
on ''X''. Concretely it may be defined as subsheaf of the sheaf of rational functionsKollár (2013), Notation 1.2.
:
That is, a nonzero rational function ''f'' is a section of over ''U'' if and only if for any prime divisor ''Z'' intersecting ''U'',
:
where ''nZ'' is the coefficient of ''Z'' in ''D''. If ''D'' is principal, so ''D'' is the divisor of a rational function ''g'', then there is an isomorphism
:
since is an effective divisor and so is regular thanks to the normality of ''X''. Conversely, if is isomorphic to as an -module, then ''D'' is principal. It follows that ''D'' is locally principal if and only if is invertible; that is, a line bundle.
If ''D'' is an effective divisor that corresponds to a subscheme of ''X'' (for example ''D'' can be a reduced divisor or a prime divisor), then the ideal sheaf of the subscheme ''D'' is equal to This leads to an often used short exact sequence
In mathematics, an exact sequence is a sequence of morphisms between objects (for example, Group (mathematics), groups, Ring (mathematics), rings, Module (mathematics), modules, and, more generally, objects of an abelian category) such that the Im ...
,
:
The sheaf cohomology of this sequence shows that contains information on whether regular functions on ''D'' are the restrictions of regular functions on ''X''.
There is also an inclusion of sheaves
:
This furnishes a canonical element of namely, the image of the global section 1. This is called the ''canonical section'' and may be denoted ''sD''. While the canonical section is the image of a nowhere vanishing rational function, its image in vanishes along ''D'' because the transition functions vanish along ''D''. When ''D'' is a smooth Cartier divisor, the cokernel of the above inclusion may be identified; see #Cartier divisors below.
Assume that ''X'' is a normal integral separated scheme of finite type over a field. Let ''D'' be a Weil divisor. Then is a rank one reflexive sheaf, and since is defined as a subsheaf of it is a fractional ideal sheaf (see below). Conversely, every rank one reflexive sheaf corresponds to a Weil divisor: The sheaf can be restricted to the regular locus, where it becomes free and so corresponds to a Cartier divisor (again, see below), and because the singular locus has codimension at least two, the closure of the Cartier divisor is a Weil divisor.
Divisor class group
The Weil divisor class group Cl(''X'') is the quotient of Div(''X'') by the subgroup of all principal Weil divisors. Two divisors are said to be linearly equivalent if their difference is principal, so the divisor class group is the group of divisors modulo linear equivalence. For a variety ''X'' of dimension ''n'' over a field, the divisor class group is aChow group
In algebraic geometry, the Chow groups (named after Wei-Liang Chow by ) of an algebraic variety over any field are algebro-geometric analogs of the homology of a topological space. The elements of the Chow group are formed out of subvarieties ...
; namely, Cl(''X'') is the Chow group CH''n''−1(''X'') of (''n''−1)-dimensional cycles.
Let ''Z'' be a closed subset of ''X''. If ''Z'' is irreducible of codimension one, then Cl(''X'' − ''Z'') is isomorphic to the quotient group of Cl(''X'') by the class of ''Z''. If ''Z'' has codimension at least 2 in ''X'', then the restriction Cl(''X'') → Cl(''X'' − ''Z'') is an isomorphism. (These facts are special cases of the localization sequence for Chow groups.)
On a normal integral Noetherian scheme ''X'', two Weil divisors ''D'', ''E'' are linearly equivalent if and only if and are isomorphic as -modules. Isomorphism classes of reflexive sheaves on ''X'' form a monoid with product given as the reflexive hull of a tensor product. Then defines a monoid isomorphism from the Weil divisor class group of ''X'' to the monoid of isomorphism classes of rank-one reflexive sheaves on ''X''.
Examples
* Let ''k'' be a field, and let ''n'' be a positive integer. Since the polynomial ring ''k'' 'x''1, ..., ''xn''is a unique factorization domain, the divisor class group of affine space A''n'' over ''k'' is equal to zero. Sinceprojective space
In mathematics, the concept of a projective space originated from the visual effect of perspective, where parallel lines seem to meet ''at infinity''. A projective space may thus be viewed as the extension of a Euclidean space, or, more generally ...
P''n'' over ''k'' minus a hyperplane ''H'' is isomorphic to A''n'', it follows that the divisor class group of P''n'' is generated by the class of ''H''. From there, it is straightforward to check that Cl(P''n'') is in fact isomorphic to the integers Z, generated by ''H''. Concretely, this means that every codimension-1 subvariety of P''n'' is defined by the vanishing of a single homogeneous polynomial.
* Let ''X'' be an algebraic curve over a field ''k''. Every closed point ''p'' in ''X'' has the form Spec ''E'' for some finite extension field ''E'' of ''k'', and the degree of ''p'' is defined to be the degree of ''E'' over ''k''. Extending this by linearity gives the notion of degree for a divisor on ''X''. If ''X'' is a projective curve over ''k'', then the divisor of a nonzero rational function ''f'' on ''X'' has degree zero. As a result, for a projective curve ''X'', the degree gives a homomorphism deg: Cl(''X'') → Z.
* For the projective line P1 over a field ''k'', the degree gives an isomorphism Cl(P1) ≅ Z. For any smooth projective curve ''X'' with a ''k''-rational point
In number theory and algebraic geometry, a rational point of an algebraic variety is a point whose coordinates belong to a given field. If the field is not mentioned, the field of rational numbers is generally understood. If the field is the fiel ...
, the degree homomorphism is surjective, and the kernel is isomorphic to the group of ''k''-points on the Jacobian variety
In mathematics, the Jacobian variety ''J''(''C'') of a non-singular algebraic curve ''C'' of genus ''g'' is the moduli space of degree 0 line bundles. It is the connected component of the identity in the Picard group of ''C'', hence an abelia ...
of ''X'', which is an abelian variety of dimension equal to the genus of ''X''. It follows, for example, that the divisor class group of a complex elliptic curve
In mathematics, an elliptic curve is a smooth, projective, algebraic curve of genus one, on which there is a specified point . An elliptic curve is defined over a field and describes points in , the Cartesian product of with itself. If the ...
is an uncountable
In mathematics, an uncountable set, informally, is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger tha ...
abelian group.
* Generalizing the previous example: for any smooth projective variety ''X'' over a field ''k'' such that ''X'' has a ''k''-rational point, the divisor class group Cl(''X'') is an extension of a finitely generated abelian group, the Néron–Severi group, by the group of ''k''-points of a connected group scheme
In mathematics, a group scheme is a type of object from algebraic geometry equipped with a composition law. Group schemes arise naturally as symmetries of schemes, and they generalize algebraic groups, in the sense that all algebraic groups hav ...
For ''k'' of characteristic zero, is an abelian variety, the Picard variety of ''X''.
*For ''R'' the ring of integers
In mathematics, the ring of integers of an algebraic number field K is the ring of all algebraic integers contained in K. An algebraic integer is a root of a monic polynomial with integer coefficients: x^n+c_x^+\cdots+c_0. This ring is often de ...
of a number field
In mathematics, an algebraic number field (or simply number field) is an extension field K of the field of rational numbers such that the field extension K / \mathbb has finite degree (and hence is an algebraic field extension).
Thus K is a ...
, the divisor class group Cl(''R'') := Cl(Spec ''R'') is also called the ideal class group
In mathematics, the ideal class group (or class group) of an algebraic number field K is the quotient group J_K/P_K where J_K is the group of fractional ideals of the ring of integers of K, and P_K is its subgroup of principal ideals. The ...
of ''R''. It is a finite abelian group. Understanding ideal class groups is a central goal of algebraic number theory
Algebraic number theory is a branch of number theory that uses the techniques of abstract algebra to study the integers, rational numbers, and their generalizations. Number-theoretic questions are expressed in terms of properties of algebraic ob ...
.
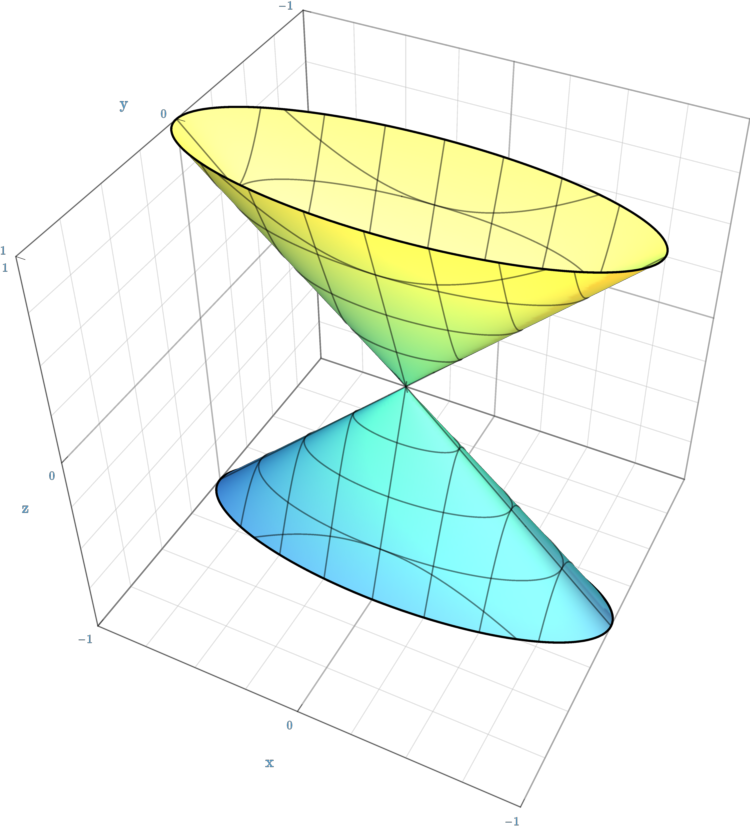
* quadric
In mathematics, a quadric or quadric surface is a generalization of conic sections (ellipses, parabolas, and hyperbolas). In three-dimensional space, quadrics include ellipsoids, paraboloids, and hyperboloids.
More generally, a quadric hype ...
cone of dimension 2, defined by the equation ''xy'' = ''z''2 in affine 3-space over a field. Then the line ''D'' in ''X'' defined by ''x'' = ''z'' = 0 is not principal on ''X'' near the origin. Note that ''D'' ''can'' be defined as a set by one equation on ''X'', namely ''x'' = 0; but the function ''x'' on ''X'' vanishes to order 2 along ''D'', and so we only find that 2''D'' is Cartier (as defined below) on ''X''. In fact, the divisor class group Cl(''X'') is isomorphic to the cyclic group Z/2, generated by the class of ''D''.
* Let ''X'' be the quadric cone of dimension 3, defined by the equation ''xy'' = ''zw'' in affine 4-space over a field. Then the plane ''D'' in ''X'' defined by ''x'' = ''z'' = 0 cannot be defined in ''X'' by one equation near the origin, even as a set. It follows that ''D'' is not Q-Cartier on ''X''; that is, no positive multiple of ''D'' is Cartier. In fact, the divisor class group Cl(''X'') is isomorphic to the integers Z, generated by the class of ''D''.
The canonical divisor
Let ''X'' be a normal variety over a perfect field. The smooth locus ''U'' of ''X'' is an open subset whose complement has codimension at least 2. Let ''j'': ''U'' → ''X'' be the inclusion map, then the restriction homomorphism: : is an isomorphism, since ''X'' − ''U'' has codimension at least 2 in ''X''. For example, one can use this isomorphism to define thecanonical divisor
The adjective canonical is applied in many contexts to mean 'according to the canon' the standard, rule or primary source that is accepted as authoritative for the body of knowledge or literature in that context. In mathematics, ''canonical examp ...
''K''''X'' of ''X'': it is the Weil divisor (up to linear equivalence) corresponding to the line bundle of differential forms of top degree on ''U''. Equivalently, the sheaf on ''X'' is the direct image sheaf where ''n'' is the dimension of ''X''.
Example: Let ''X'' = P''n'' be the projective ''n''-space with the homogeneous coordinates ''x''0, ..., ''xn''. Let ''U'' = . Then ''U'' is isomorphic to the affine ''n''-space with the coordinates ''yi'' = ''xi''/''x''0. Let
:
Then ω is a rational differential form on ''U''; thus, it is a rational section of which has simple poles along ''Zi'' = , ''i'' = 1, ..., ''n''. Switching to a different affine chart changes only the sign of ω and so we see ω has a simple pole along ''Z''0 as well. Thus, the divisor of ω is
:
and its divisor class is
: