diffuse lepromatous leprosy on:
[Wikipedia]
[Google]
[Amazon]

 Diffusion is the net movement of anything (for example, atoms, ions, molecules, energy) generally from a region of higher
Diffusion is the net movement of anything (for example, atoms, ions, molecules, energy) generally from a region of higher
 The concept of diffusion is widely used in:
The concept of diffusion is widely used in:
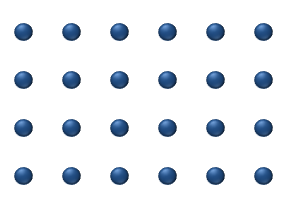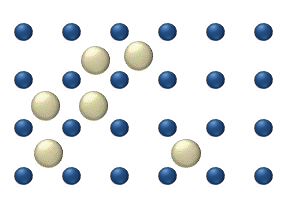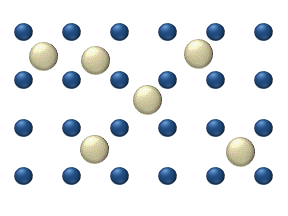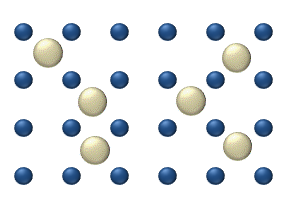 Diffusion of reagents on the surface of a
Diffusion of reagents on the surface of a
 Diffusion is the net movement of anything (for example, atoms, ions, molecules, energy) generally from a region of higher
Diffusion is the net movement of anything (for example, atoms, ions, molecules, energy) generally from a region of higher concentration
In chemistry, concentration is the abundance of a constituent divided by the total volume of a mixture. Several types of mathematical description can be distinguished: '' mass concentration'', ''molar concentration'', ''number concentration'', an ...
to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy
In thermodynamics, the Gibbs free energy (or Gibbs energy; symbol G) is a thermodynamic potential that can be used to calculate the maximum amount of work that may be performed by a thermodynamically closed system at constant temperature and pr ...
or chemical potential
In thermodynamics, the chemical potential of a species is the energy that can be absorbed or released due to a change of the particle number of the given species, e.g. in a chemical reaction or phase transition. The chemical potential of a species ...
. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, like in spinodal decomposition
Spinodal decomposition is a mechanism by which a single thermodynamic phase spontaneously separates into two phases (without nucleation). Decomposition occurs when there is no thermodynamic barrier to phase separation. As a result, phase separatio ...
.
The concept of diffusion is widely used in many fields, including physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which r ...
(particle diffusion
In mathematics and physics, the heat equation is a certain partial differential equation. Solutions of the heat equation are sometimes known as caloric functions. The theory of the heat equation was first developed by Joseph Fourier in 1822 fo ...
), chemistry
Chemistry is the science, scientific study of the properties and behavior of matter. It is a natural science that covers the Chemical element, elements that make up matter to the chemical compound, compounds made of atoms, molecules and ions ...
, biology
Biology is the scientific study of life. It is a natural science with a broad scope but has several unifying themes that tie it together as a single, coherent field. For instance, all organisms are made up of cells that process hereditary i ...
, sociology
Sociology is a social science that focuses on society, human social behavior, patterns of Interpersonal ties, social relationships, social interaction, and aspects of culture associated with everyday life. It uses various methods of Empirical ...
, economics
Economics () is the social science that studies the Production (economics), production, distribution (economics), distribution, and Consumption (economics), consumption of goods and services.
Economics focuses on the behaviour and intera ...
, and finance
Finance is the study and discipline of money, currency and capital assets. It is related to, but not synonymous with economics, the study of production, distribution, and consumption of money, assets, goods and services (the discipline of fina ...
(diffusion of people, ideas, and price values). The central idea of diffusion, however, is common to all of these: a substance or collection undergoing diffusion spreads out from a point or location at which there is a higher concentration of that substance or collection.
A gradient
In vector calculus, the gradient of a scalar-valued differentiable function of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p is the "direction and rate of fastest increase". If the gradi ...
is the change in the value of a quantity, for example, concentration, pressure
Pressure (symbol: ''p'' or ''P'') is the force applied perpendicular to the surface of an object per unit area over which that force is distributed. Gauge pressure (also spelled ''gage'' pressure)The preferred spelling varies by country and e ...
, or temperature
Temperature is a physical quantity that expresses quantitatively the perceptions of hotness and coldness. Temperature is measured with a thermometer.
Thermometers are calibrated in various temperature scales that historically have relied o ...
with the change in another variable, usually distance
Distance is a numerical or occasionally qualitative measurement of how far apart objects or points are. In physics or everyday usage, distance may refer to a physical length or an estimation based on other criteria (e.g. "two counties over"). ...
. A change in concentration over a distance is called a concentration gradient
Molecular diffusion, often simply called diffusion, is the thermal motion of all (liquid or gas) particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size (mass) of ...
, a change in pressure over a distance is called a pressure gradient
In atmospheric science, the pressure gradient (typically of Earth's atmosphere, air but more generally of any fluid) is a physical quantity that describes in which direction and at what rate the pressure increases the most rapidly around a particu ...
, and a change in temperature over a distance is called a temperature gradient
A temperature gradient is a physical quantity that describes in which direction and at what rate the temperature changes the most rapidly around a particular location. The temperature gradient is a dimensional quantity expressed in units of degree ...
.
The word ''diffusion'' derives from the Latin
Latin (, or , ) is a classical language belonging to the Italic branch of the Indo-European languages. Latin was originally a dialect spoken in the lower Tiber area (then known as Latium) around present-day Rome, but through the power of the ...
word, ''diffundere'', which means "to spread out."
A distinguishing feature of diffusion is that it depends on particle random walk
In mathematics, a random walk is a random process that describes a path that consists of a succession of random steps on some mathematical space.
An elementary example of a random walk is the random walk on the integer number line \mathbb Z ...
, and results in mixing or mass transport without requiring directed bulk motion. Bulk motion, or bulk flow, is the characteristic of advection
In the field of physics, engineering, and earth sciences, advection is the transport of a substance or quantity by bulk motion of a fluid. The properties of that substance are carried with it. Generally the majority of the advected substance is al ...
. The term convection
Convection is single or multiphase fluid flow that occurs spontaneously due to the combined effects of material property heterogeneity and body forces on a fluid, most commonly density and gravity (see buoyancy). When the cause of the convec ...
is used to describe the combination of both transport phenomena
In engineering, physics, and chemistry, the study of transport phenomena concerns the exchange of mass, energy, charge, momentum and angular momentum between observed and studied systems. While it draws from fields as diverse as continuum mechan ...
.
If a diffusion process can be described by Fick's laws, it's called a normal diffusion (or Fickian diffusion); Otherwise, it's called an anomalous diffusion
Anomalous diffusion is a diffusion process with a non-linear relationship between the mean squared displacement (MSD), \langle r^(\tau )\rangle , and time. This behavior is in stark contrast to Brownian motion, the typical diffusion process descri ...
(or non-Fickian diffusion).
When talking about the extent of diffusion, two length scales are used in two different scenarios:
# Brownian motion
Brownian motion, or pedesis (from grc, πήδησις "leaping"), is the random motion of particles suspended in a medium (a liquid or a gas).
This pattern of motion typically consists of random fluctuations in a particle's position insi ...
of an impulsive point source (for example, one single spray of perfume)—the square root of the mean squared displacement
In statistical mechanics, the mean squared displacement (MSD, also mean square displacement, average squared displacement, or mean square fluctuation) is a measure of the deviation of the position of a particle with respect to a reference positi ...
from this point. In Fickian diffusion, this is , where is the dimension
In physics and mathematics, the dimension of a Space (mathematics), mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any Point (geometry), point within it. Thus, a Line (geometry), lin ...
of this Brownian motion;
# Constant concentration source in one dimension—the diffusion length. In Fickian diffusion, this is .
Diffusion vs. bulk flow
"Bulk flow" is the movement/flow of an entire body due to a pressure gradient (for example, water coming out of a tap). "Diffusion" is the gradual movement/dispersion of concentration within a body, due to a concentration gradient, with no net movement of matter. An example of a process where both bulk motion and diffusion occur is human breathing. First, there is a "bulk flow" process. Thelungs
The lungs are the primary organs of the respiratory system in humans and most other animals, including some snails and a small number of fish. In mammals and most other vertebrates, two lungs are located near the backbone on either side of th ...
are located in the thoracic cavity
The thoracic cavity (or chest cavity) is the chamber of the body of vertebrates that is protected by the thoracic wall (rib cage and associated skin, muscle, and fascia). The central compartment of the thoracic cavity is the mediastinum. There ...
, which expands as the first step in external respiration. This expansion leads to an increase in volume of the alveoli Alveolus (; pl. alveoli, adj. alveolar) is a general anatomical term for a concave cavity or pit.
Uses in anatomy and zoology
* Pulmonary alveolus, an air sac in the lungs
** Alveolar cell or pneumocyte
** Alveolar duct
** Alveolar macrophage
* ...
in the lungs, which causes a decrease in pressure in the alveoli. This creates a pressure gradient between the air
The atmosphere of Earth is the layer of gases, known collectively as air, retained by Earth's gravity that surrounds the planet and forms its planetary atmosphere. The atmosphere of Earth protects life on Earth by creating pressure allowing f ...
outside the body at relatively high pressure and the alveoli at relatively low pressure. The air moves down the pressure gradient through the airways of the lungs and into the alveoli until the pressure of the air and that in the alveoli are equal, that is, the movement of air by bulk flow stops once there is no longer a pressure gradient.
Second, there is a "diffusion" process. The air arriving in the alveoli has a higher concentration of oxygen than the "stale" air in the alveoli. The increase in oxygen concentration creates a concentration gradient for oxygen between the air in the alveoli and the blood in the capillaries
A capillary is a small blood vessel from 5 to 10 micrometres (μm) in diameter. Capillaries are composed of only the tunica intima, consisting of a thin wall of simple squamous endothelial cells. They are the smallest blood vessels in the body: ...
that surround the alveoli. Oxygen then moves by diffusion, down the concentration gradient, into the blood. The other consequence of the air arriving in alveoli is that the concentration of carbon dioxide
Carbon dioxide (chemical formula ) is a chemical compound made up of molecules that each have one carbon atom covalently double bonded to two oxygen atoms. It is found in the gas state at room temperature. In the air, carbon dioxide is transpar ...
in the alveoli decreases. This creates a concentration gradient for carbon dioxide to diffuse from the blood into the alveoli, as fresh air has a very low concentration of carbon dioxide compared to the blood
Blood is a body fluid in the circulatory system of humans and other vertebrates that delivers necessary substances such as nutrients and oxygen to the cells, and transports metabolic waste products away from those same cells. Blood in the c ...
in the body.
Third, there is another "bulk flow" process. The pumping action of the heart
The heart is a muscular organ in most animals. This organ pumps blood through the blood vessels of the circulatory system. The pumped blood carries oxygen and nutrients to the body, while carrying metabolic waste such as carbon dioxide t ...
then transports the blood around the body. As the left ventricle of the heart contracts, the volume decreases, which increases the pressure in the ventricle. This creates a pressure gradient between the heart and the capillaries, and blood moves through blood vessel
The blood vessels are the components of the circulatory system that transport blood throughout the human body. These vessels transport blood cells, nutrients, and oxygen to the tissues of the body. They also take waste and carbon dioxide away ...
s by bulk flow down the pressure gradient.
Diffusion in the context of different disciplines
 The concept of diffusion is widely used in:
The concept of diffusion is widely used in: physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which r ...
(particle diffusion
In mathematics and physics, the heat equation is a certain partial differential equation. Solutions of the heat equation are sometimes known as caloric functions. The theory of the heat equation was first developed by Joseph Fourier in 1822 fo ...
), chemistry
Chemistry is the science, scientific study of the properties and behavior of matter. It is a natural science that covers the Chemical element, elements that make up matter to the chemical compound, compounds made of atoms, molecules and ions ...
, biology
Biology is the scientific study of life. It is a natural science with a broad scope but has several unifying themes that tie it together as a single, coherent field. For instance, all organisms are made up of cells that process hereditary i ...
, sociology
Sociology is a social science that focuses on society, human social behavior, patterns of Interpersonal ties, social relationships, social interaction, and aspects of culture associated with everyday life. It uses various methods of Empirical ...
, economics
Economics () is the social science that studies the Production (economics), production, distribution (economics), distribution, and Consumption (economics), consumption of goods and services.
Economics focuses on the behaviour and intera ...
, and finance
Finance is the study and discipline of money, currency and capital assets. It is related to, but not synonymous with economics, the study of production, distribution, and consumption of money, assets, goods and services (the discipline of fina ...
(diffusion of people, ideas and of price values). However, in each case the substance or collection undergoing diffusion is "spreading out" from a point or location at which there is a higher concentration of that substance or collection.
There are two ways to introduce the notion of ''diffusion'': either a phenomenological approach starting with Fick's laws of diffusion
Fick's laws of diffusion describe diffusion and were derived by Adolf Fick in 1855. They can be used to solve for the diffusion coefficient, . Fick's first law can be used to derive his second law which in turn is identical to the diffusion equ ...
and their mathematical consequences, or a physical and atomistic one, by considering the ''random walk
In mathematics, a random walk is a random process that describes a path that consists of a succession of random steps on some mathematical space.
An elementary example of a random walk is the random walk on the integer number line \mathbb Z ...
of the diffusing particles''.
In the phenomenological approach, ''diffusion is the movement of a substance from a region of high concentration to a region of low concentration without bulk motion''. According to Fick's laws, the diffusion flux
Flux describes any effect that appears to pass or travel (whether it actually moves or not) through a surface or substance. Flux is a concept in applied mathematics and vector calculus which has many applications to physics. For transport ph ...
is proportional to the negative gradient
In vector calculus, the gradient of a scalar-valued differentiable function of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p is the "direction and rate of fastest increase". If the gradi ...
of concentrations. It goes from regions of higher concentration to regions of lower concentration. Sometime later, various generalizations of Fick's laws were developed in the frame of thermodynamics
Thermodynamics is a branch of physics that deals with heat, work, and temperature, and their relation to energy, entropy, and the physical properties of matter and radiation. The behavior of these quantities is governed by the four laws of the ...
and non-equilibrium thermodynamics
Non-equilibrium thermodynamics is a branch of thermodynamics that deals with physical systems that are not in thermodynamic equilibrium but can be described in terms of macroscopic quantities (non-equilibrium state variables) that represent an ext ...
.
From the ''atomistic point of view'', diffusion is considered as a result of the random walk of the diffusing particles. In molecular diffusion
Molecular diffusion, often simply called diffusion, is the thermal motion of all (liquid or gas) particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size (mass) of ...
, the moving molecules are self-propelled by thermal energy. Random walk of small particles in suspension in a fluid was discovered in 1827 by Robert Brown, who found that minute particle suspended in a liquid medium and just large enough to be visible under an optical microscope exhibit a rapid and continually irregular motion of particles known as Brownian movement. The theory of the Brownian motion
Brownian motion, or pedesis (from grc, πήδησις "leaping"), is the random motion of particles suspended in a medium (a liquid or a gas).
This pattern of motion typically consists of random fluctuations in a particle's position insi ...
and the atomistic backgrounds of diffusion were developed by Albert Einstein
Albert Einstein ( ; ; 14 March 1879 – 18 April 1955) was a German-born theoretical physicist, widely acknowledged to be one of the greatest and most influential physicists of all time. Einstein is best known for developing the theory ...
.
The concept of diffusion is typically applied to any subject matter involving random walks in ensembles of individuals.
In chemistry
Chemistry is the science, scientific study of the properties and behavior of matter. It is a natural science that covers the Chemical element, elements that make up matter to the chemical compound, compounds made of atoms, molecules and ions ...
and materials science, diffusion refers to the movement of fluid molecules in porous solids. Molecular diffusion
Molecular diffusion, often simply called diffusion, is the thermal motion of all (liquid or gas) particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size (mass) of ...
occurs when the collision with another molecule is more likely than the collision with the pore walls. Under such conditions, the diffusivity is similar to that in a non-confined space and is proportional to the mean free path. Knudsen diffusion
In physics, Knudsen diffusion, named after Martin Knudsen, is a means of diffusion that occurs when the scale length of a system is comparable to or smaller than the mean free path of the particles involved. An example of this is in a long pore wi ...
, which occurs when the pore diameter is comparable to or smaller than the mean free path of the molecule diffusing through the pore. Under this condition, the collision with the pore walls becomes gradually more likely and the diffusivity is lower. Finally there is configurational diffusion, which happens if the molecules have comparable size to that of the pore. Under this condition, the diffusivity is much lower compared to molecular diffusion and small differences in the kinetic diameter of the molecule cause large differences in diffusivity
Diffusivity is a rate of diffusion, a measure of the rate at which particles or heat or fluids can spread.
It is measured differently for different mediums.
Diffusivity may refer to:
*Thermal diffusivity, diffusivity of heat
*Diffusivity of mass: ...
.
Biologist
A biologist is a scientist who conducts research in biology. Biologists are interested in studying life on Earth, whether it is an individual Cell (biology), cell, a multicellular organism, or a Community (ecology), community of Biological inter ...
s often use the terms "net movement" or "net diffusion" to describe the movement of ions or molecules by diffusion. For example, oxygen can diffuse through cell membranes so long as there is a higher concentration of oxygen outside the cell. However, because the movement of molecules is random, occasionally oxygen molecules move out of the cell (against the concentration gradient). Because there are more oxygen molecules outside the cell, the probability
Probability is the branch of mathematics concerning numerical descriptions of how likely an Event (probability theory), event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and ...
that oxygen molecules will enter the cell is higher than the probability that oxygen molecules will leave the cell. Therefore, the "net" movement of oxygen molecules (the difference between the number of molecules either entering or leaving the cell) is into the cell. In other words, there is a ''net movement'' of oxygen molecules down the concentration gradient.
History of diffusion in physics
In the scope of time, diffusion in solids was used long before the theory of diffusion was created. For example,Pliny the Elder
Gaius Plinius Secundus (AD 23/2479), called Pliny the Elder (), was a Roman author, naturalist and natural philosopher, and naval and army commander of the early Roman Empire, and a friend of the emperor Vespasian. He wrote the encyclopedic '' ...
had previously described the cementation process
The cementation process is an obsolete technology for making steel by carburization of iron. Unlike modern steelmaking, it increased the amount of carbon in the iron. It was apparently developed before the 17th century. Derwentcote Steel F ...
, which produces steel from the element iron
Iron () is a chemical element with symbol Fe (from la, ferrum) and atomic number 26. It is a metal that belongs to the first transition series and group 8 of the periodic table. It is, by mass, the most common element on Earth, right in f ...
(Fe) through carbon diffusion. Another example is well known for many centuries, the diffusion of colors of stained glass
Stained glass is coloured glass as a material or works created from it. Throughout its thousand-year history, the term has been applied almost exclusively to the windows of churches and other significant religious buildings. Although tradition ...
or earthenware
Earthenware is glazed or unglazed nonvitreous pottery that has normally been fired below . Basic earthenware, often called terracotta, absorbs liquids such as water. However, earthenware can be made impervious to liquids by coating it with a ce ...
and Chinese ceramics
Chinese ceramics show a continuous development since pre-dynastic times and are one of the most significant forms of Chinese art and ceramics globally. The first pottery was made during the Palaeolithic era. Chinese ceramics range from construc ...
.
In modern science, the first systematic experimental study of diffusion was performed by Thomas Graham. He studied diffusion in gases, and the main phenomenon was described by him in 1831–1833:
"...gases of different nature, when brought into contact, do not arrange themselves according to their density, the heaviest undermost, and the lighter uppermost, but they spontaneously diffuse, mutually and equally, through each other, and so remain in the intimate state of mixture for any length of time."The measurements of Graham contributed to
James Clerk Maxwell
James Clerk Maxwell (13 June 1831 – 5 November 1879) was a Scottish mathematician and scientist responsible for the classical theory of electromagnetic radiation, which was the first theory to describe electricity, magnetism and ligh ...
deriving, in 1867, the coefficient of diffusion for CO2 in the air. The error rate is less than 5%.
In 1855, Adolf Fick
Adolf Eugen Fick (3 September 1829 – 21 August 1901) was a German-born physician and physiologist.
Early life and education
Fick began his work in the formal study of mathematics and physics before realising an aptitude for medicine. He th ...
, the 26-year-old anatomy demonstrator from Zürich, proposed his law of diffusion. He used Graham's research, stating his goal as "the development of a fundamental law, for the operation of diffusion in a single element of space". He asserted a deep analogy between diffusion and conduction of heat or electricity, creating a formalism similar to Fourier's law for heat conduction (1822) and Ohm's law
Ohm's law states that the current through a conductor between two points is directly proportional to the voltage across the two points. Introducing the constant of proportionality, the resistance, one arrives at the usual mathematical equat ...
for electric current (1827).
Robert Boyle
Robert Boyle (; 25 January 1627 – 31 December 1691) was an Anglo-Irish natural philosopher, chemist, physicist, alchemist and inventor. Boyle is largely regarded today as the first modern chemist, and therefore one of the founders of ...
demonstrated diffusion in solids in the 17th century by penetration of zinc into a copper coin. Nevertheless, diffusion in solids was not systematically studied until the second part of the 19th century. William Chandler Roberts-Austen
Sir William Chandler Roberts-Austen (3 March 1843, Kennington – 22 November 1902, London) was an English metallurgist noted for his research on the physical properties of metals and their alloys. The austenite class of iron alloys is named aft ...
, the well-known British metallurgist and former assistant of Thomas Graham studied systematically solid state diffusion on the example of gold in lead in 1896. :
"... My long connection with Graham's researches made it almost a duty to attempt to extend his work on liquid diffusion to metals."In 1858,
Rudolf Clausius
Rudolf Julius Emanuel Clausius (; 2 January 1822 – 24 August 1888) was a German physicist and mathematician and is considered one of the central founding fathers of the science of thermodynamics. By his restatement of Sadi Carnot's principle ...
introduced the concept of the mean free path
In physics, mean free path is the average distance over which a moving particle (such as an atom, a molecule, or a photon) travels before substantially changing its direction or energy (or, in a specific context, other properties), typically as a ...
. In the same year, James Clerk Maxwell
James Clerk Maxwell (13 June 1831 – 5 November 1879) was a Scottish mathematician and scientist responsible for the classical theory of electromagnetic radiation, which was the first theory to describe electricity, magnetism and ligh ...
developed the first atomistic theory of transport processes in gases. The modern atomistic theory of diffusion and Brownian motion
Brownian motion, or pedesis (from grc, πήδησις "leaping"), is the random motion of particles suspended in a medium (a liquid or a gas).
This pattern of motion typically consists of random fluctuations in a particle's position insi ...
was developed by Albert Einstein
Albert Einstein ( ; ; 14 March 1879 – 18 April 1955) was a German-born theoretical physicist, widely acknowledged to be one of the greatest and most influential physicists of all time. Einstein is best known for developing the theory ...
, Marian Smoluchowski
Marian Smoluchowski (; 28 May 1872 – 5 September 1917) was a Polish physicist who worked in the Polish territories of the Austro-Hungarian Empire. He was a pioneer of statistical physics, and an avid mountaineer.
Life
Born into an upper-c ...
and Jean-Baptiste Perrin
Jean Baptiste Perrin (30 September 1870 – 17 April 1942) was a French physicist who, in his studies of the Brownian motion of minute particles suspended in liquids ( sedimentation equilibrium), verified Albert Einstein’s explanation of this ...
. Ludwig Boltzmann
Ludwig Eduard Boltzmann (; 20 February 1844 – 5 September 1906) was an Austrian physicist and philosopher. His greatest achievements were the development of statistical mechanics, and the statistical explanation of the second law of thermodyn ...
, in the development of the atomistic backgrounds of the macroscopic transport processes, introduced the Boltzmann equation
The Boltzmann equation or Boltzmann transport equation (BTE) describes the statistical behaviour of a thermodynamic system not in a state of equilibrium, devised by Ludwig Boltzmann in 1872.Encyclopaedia of Physics (2nd Edition), R. G. Lerne ...
, which has served mathematics and physics with a source of transport process ideas and concerns for more than 140 years.S. Chapman, T. G. Cowling (1970) ''The Mathematical Theory of Non-uniform Gases: An Account of the Kinetic Theory of Viscosity, Thermal Conduction and Diffusion in Gases'', Cambridge University Press (3rd edition), .
In 1920–1921, George de Hevesy
George Charles de Hevesy (born György Bischitz; hu, Hevesy György Károly; german: Georg Karl von Hevesy; 1 August 1885 – 5 July 1966) was a Hungarian radiochemist and Nobel Prize in Chemistry laureate, recognized in 1943 for his key role ...
measured self-diffusion According to IUPAC definition, self-diffusion coefficient is the diffusion coefficient D_i^* of species i when the chemical potential gradient equals zero. It is linked to the diffusion coefficient D_i by the equation:
D_i^*=D_i\frac.
Here, a_i is ...
using radioisotope
A radionuclide (radioactive nuclide, radioisotope or radioactive isotope) is a nuclide that has excess nuclear energy, making it unstable. This excess energy can be used in one of three ways: emitted from the nucleus as gamma radiation; transferr ...
s. He studied self-diffusion of radioactive isotopes of lead in the liquid and solid lead.
Yakov Frenkel
__NOTOC__
Yakov Il'ich Frenkel (russian: Яков Ильич Френкель; 10 February 1894 – 23 January 1952) was a Soviet physicist renowned for his works in the field of condensed matter physics. He is also known as Jacov Frenkel, frequ ...
(sometimes, Jakov/Jacob Frenkel) proposed, and elaborated in 1926, the idea of diffusion in crystals through local defects (vacancies and interstitial
An interstitial space or interstice is a space between structures or objects.
In particular, interstitial may refer to:
Biology
* Interstitial cell tumor
* Interstitial cell, any cell that lies between other cells
* Interstitial collagenase ...
atoms). He concluded, the diffusion process in condensed matter is an ensemble of elementary jumps and quasichemical interactions of particles and defects. He introduced several mechanisms of diffusion and found rate constants from experimental data.
Sometime later, Carl Wagner
Carl Wilhelm Wagner (May 25, 1901 – December 10, 1977) was a German Physical chemist. He is best known for his pioneering work on Solid-state chemistry, where his work on oxidation rate theory, counter diffusion of ions and defect chemistry ...
and Walter H. Schottky
Walter Hans Schottky (23 July 1886 – 4 March 1976) was a German physicist who played a major early role in developing the theory of electron and ion emission phenomena, invented the screen-grid vacuum tube in 1915 while working at Siemens ...
developed Frenkel's ideas about mechanisms of diffusion further. Presently, it is universally recognized that atomic defects are necessary to mediate diffusion in crystals.
Henry Eyring, with co-authors, applied his theory of absolute reaction rates to Frenkel's quasichemical model of diffusion. The analogy between reaction kinetics
Chemical kinetics, also known as reaction kinetics, is the branch of physical chemistry that is concerned with understanding the rates of chemical reactions. It is to be contrasted with chemical thermodynamics, which deals with the direction in w ...
and diffusion leads to various nonlinear versions of Fick's law.
Basic models of diffusion
Diffusion flux
Each model of diffusion expresses the diffusion flux with the use of concentrations, densities and their derivatives. Flux is a vector representing the quantity and direction of transfer. Given a smallarea
Area is the quantity that expresses the extent of a region on the plane or on a curved surface. The area of a plane region or ''plane area'' refers to the area of a shape
A shape or figure is a graphics, graphical representation of an obje ...
with normal , the transfer of a physical quantity
A physical quantity is a physical property of a material or system that can be quantified by measurement. A physical quantity can be expressed as a ''value'', which is the algebraic multiplication of a ' Numerical value ' and a ' Unit '. For examp ...
through the area per time is
:
where is the inner product
In mathematics, an inner product space (or, rarely, a Hausdorff space, Hausdorff pre-Hilbert space) is a real vector space or a complex vector space with an operation (mathematics), operation called an inner product. The inner product of two ve ...
and is the little-o notation
Big ''O'' notation is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity. Big O is a member of a family of notations invented by Paul Bachmann, Edmund Land ...
. If we use the notation of vector area In 3-dimensional geometry and vector calculus, an area vector is a vector combining an area quantity with a direction, thus representing an ''oriented area'' in three dimensions.
Every bounded surface in three dimensions can be associated with a ...
then
:
The dimension
In physics and mathematics, the dimension of a Space (mathematics), mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any Point (geometry), point within it. Thus, a Line (geometry), lin ...
of the diffusion flux is luxnbsp;= uantity( ime�rea
REA or Rea may refer to:
Places
* Rea, Lombardy, in Italy
* Rea, Missouri, United States
* River Rea, a river in Birmingham, England
* River Rea, Shropshire, a river in Shropshire, England
* Rea, Hungarian name of Reea village in Totești Commun ...
. The diffusing physical quantity may be the number of particles, mass, energy, electric charge, or any other scalar extensive quantity
Physical properties of materials and systems can often be categorized as being either intensive or extensive, according to how the property changes when the size (or extent) of the system changes. According to IUPAC, an intensive quantity is one ...
. For its density, , the diffusion equation has the form
:
where is intensity of any local source of this quantity (for example, the rate of a chemical reaction).
For the diffusion equation, the no-flux boundary conditions can be formulated as on the boundary, where is the normal to the boundary at point .
Fick's law and equations
Fick's first law: the diffusion flux is proportional to the negative of the concentration gradient: : The corresponding diffusion equation (Fick's second law) is : where is theLaplace operator
In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a scalar function on Euclidean space. It is usually denoted by the symbols \nabla\cdot\nabla, \nabla^2 (where \nabla is the ...
,
:
Onsager's equations for multicomponent diffusion and thermodiffusion
Fick's law describes diffusion of an admixture in a medium. The concentration of this admixture should be small and the gradient of this concentration should be also small. The driving force of diffusion in Fick's law is the antigradient of concentration, . In 1931,Lars Onsager
Lars Onsager (November 27, 1903 – October 5, 1976) was a Norwegian-born American physical chemist and theoretical physicist. He held the Gibbs Professorship of Theoretical Chemistry at Yale University. He was awarded the Nobel Prize in Che ...
included the multicomponent transport processes in the general context of linear non-equilibrium thermodynamics. For
multi-component transport,
:
where is the flux of the ''i''th physical quantity (component) and is the ''j''th thermodynamic force.
The thermodynamic forces for the transport processes were introduced by Onsager as the space gradients of the derivatives of the entropy
Entropy is a scientific concept, as well as a measurable physical property, that is most commonly associated with a state of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynam ...
density (he used the term "force" in quotation marks or "driving force"):
:
where are the "thermodynamic coordinates".
For the heat and mass transfer one can take (the density of internal energy) and is the concentration of the th component. The corresponding driving forces are the space vectors
: because
where ''T'' is the absolute temperature and is the chemical potential of the th component. It should be stressed that the separate diffusion equations describe the mixing or mass transport without bulk motion. Therefore, the terms with variation of the total pressure are neglected. It is possible for diffusion of small admixtures and for small gradients.
For the linear Onsager equations, we must take the thermodynamic forces in the linear approximation near equilibrium:
:
where the derivatives of are calculated at equilibrium .
The matrix of the ''kinetic coefficients'' should be symmetric (Onsager reciprocal relations
In thermodynamics, the Onsager reciprocal relations express the equality of certain ratios between flows and forces in thermodynamic systems out of equilibrium, but where a notion of local equilibrium exists.
"Reciprocal relations" occur betw ...
) and positive definite In mathematics, positive definiteness is a property of any object to which a bilinear form or a sesquilinear form may be naturally associated, which is positive-definite. See, in particular:
* Positive-definite bilinear form
* Positive-definite f ...
( for the entropy growth).
The transport equations are
:
Here, all the indexes are related to the internal energy (0) and various components. The expression in the square brackets is the matrix of the diffusion (''i'',''k'' > 0), thermodiffusion (''i'' > 0, ''k'' = 0 or ''k'' > 0, ''i'' = 0) and thermal conductivity
The thermal conductivity of a material is a measure of its ability to conduct heat. It is commonly denoted by k, \lambda, or \kappa.
Heat transfer occurs at a lower rate in materials of low thermal conductivity than in materials of high thermal ...
() coefficients.
Under isothermal conditions ''T'' = constant. The relevant thermodynamic potential is the free energy (or the free entropy
A thermodynamic free entropy is an entropic thermodynamic potential analogous to the free energy. Also known as a Massieu, Planck, or Massieu–Planck potentials (or functions), or (rarely) free information. In statistical mechanics, free entrop ...
). The thermodynamic driving forces for the isothermal diffusion are antigradients of chemical potentials, , and the matrix of diffusion coefficients is
:
(''i,k'' > 0).
There is intrinsic arbitrariness in the definition of the thermodynamic forces and kinetic coefficients because they are not measurable separately and only their combinations can be measured. For example, in the original work of Onsager the thermodynamic forces include additional multiplier ''T'', whereas in the Course of Theoretical Physics
The ''Course of Theoretical Physics'' is a ten-volume series of books covering theoretical physics that was initiated by Lev Landau and written in collaboration with his student Evgeny Lifshitz starting in the late 1930s.
It is said that Landau ...
this multiplier is omitted but the sign of the thermodynamic forces is opposite. All these changes are supplemented by the corresponding changes in the coefficients and do not affect the measurable quantities.
Nondiagonal diffusion must be nonlinear
The formalism of linear irreversible thermodynamics (Onsager) generates the systems of linear diffusion equations in the form : If the matrix of diffusion coefficients is diagonal, then this system of equations is just a collection of decoupled Fick's equations for various components. Assume that diffusion is non-diagonal, for example, , and consider the state with . At this state, . If at some points, then becomes negative at these points in a short time. Therefore, linear non-diagonal diffusion does not preserve positivity of concentrations. Non-diagonal equations of multicomponent diffusion must be non-linear.Einstein's mobility and Teorell formula
TheEinstein relation (kinetic theory)
In physics (specifically, the kinetic theory of gases), the Einstein relation is a previously unexpected connection revealed independently by William Sutherland in 1904, Albert Einstein in 1905, and by Marian Smoluchowski in 1906 in their works on ...
connects the diffusion coefficient and the mobility (the ratio of the particle's terminal drift velocity
In physics, a drift velocity is the average velocity attained by charged particles, such as electrons, in a material due to an electric field. In general, an electron in a conductor will propagate randomly at the Fermi velocity, resulting in an a ...
to an applied force
In physics, a force is an influence that can change the motion of an object. A force can cause an object with mass to change its velocity (e.g. moving from a state of rest), i.e., to accelerate. Force can also be described intuitively as a p ...
)
:
where ''D'' is the diffusion constant
Fick's laws of diffusion describe diffusion and were derived by Adolf Fick in 1855. They can be used to solve for the diffusion coefficient, . Fick's first law can be used to derive his second law which in turn is identical to the diffusion equ ...
, ''μ'' is the "mobility", ''k''B is Boltzmann's constant
The Boltzmann constant ( or ) is the proportionality factor that relates the average relative kinetic energy of particles in a gas with the thermodynamic temperature of the gas. It occurs in the definitions of the kelvin and the gas constant, ...
, ''T'' is the absolute temperature
Thermodynamic temperature is a quantity defined in thermodynamics as distinct from kinetic theory or statistical mechanics.
Historically, thermodynamic temperature was defined by Kelvin in terms of a macroscopic relation between thermodynamic wor ...
, and ''q'' is the elementary charge
The elementary charge, usually denoted by is the electric charge carried by a single proton or, equivalently, the magnitude of the negative electric charge carried by a single electron, which has charge −1 . This elementary charge is a fundame ...
, that is, the charge of one electron.
Below, to combine in the same formula the chemical potential ''μ'' and the mobility, we use for mobility the notation .
The mobility-based approach was further applied by T. Teorell. In 1935, he studied the diffusion of ions through a membrane. He formulated the essence of his approach in the formula:
:the flux is equal to mobility × concentration × force per gram-ion.
This is the so-called ''Teorell formula''. The term "gram-ion" ("gram-particle") is used for a quantity of a substance that contains Avogadro's number
The Avogadro constant, commonly denoted or , is the proportionality factor that relates the number of constituent particles (usually molecules, atoms or ions) in a sample with the amount of substance in that sample. It is an SI defining co ...
of ions (particles). The common modern term is mole
Mole (or Molé) may refer to:
Animals
* Mole (animal) or "true mole", mammals in the family Talpidae, found in Eurasia and North America
* Golden moles, southern African mammals in the family Chrysochloridae, similar to but unrelated to Talpida ...
.
The force under isothermal conditions consists of two parts:
# Diffusion force caused by concentration gradient: .
# Electrostatic force caused by electric potential gradient: .
Here ''R'' is the gas constant, ''T'' is the absolute temperature, ''n'' is the concentration, the equilibrium concentration is marked by a superscript "eq", ''q'' is the charge and ''φ'' is the electric potential.
The simple but crucial difference between the Teorell formula and the Onsager laws is the concentration factor in the Teorell expression for the flux. In the Einstein–Teorell approach, if for the finite force the concentration tends to zero then the flux also tends to zero, whereas the Onsager equations violate this simple and physically obvious rule.
The general formulation of the Teorell formula for non-perfect systems under isothermal conditions is
:
where ''μ'' is the chemical potential
In thermodynamics, the chemical potential of a species is the energy that can be absorbed or released due to a change of the particle number of the given species, e.g. in a chemical reaction or phase transition. The chemical potential of a species ...
, ''μ''0 is the standard value of the chemical potential.
The expression is the so-called activity. It measures the "effective concentration" of a species in a non-ideal mixture. In this notation, the Teorell formula for the flux has a very simple form
:
The standard derivation of the activity includes a normalization factor and for small concentrations , where is the standard concentration. Therefore, this formula for the flux describes the flux of the normalized dimensionless quantity :
:
Fluctuation-dissipation theorem
Fluctuation-dissipation theorem
The fluctuation–dissipation theorem (FDT) or fluctuation–dissipation relation (FDR) is a powerful tool in statistical physics for predicting the behavior of systems that obey detailed balance. Given that a system obeys detailed balance, the th ...
based on the Langevin equation is developed to extend the Einstein model to the ballistic time scale. According to Langevin, the equation is based on Newton's second law of motion as
:
where
* ''x'' is the position.
* ''μ'' is the mobility of the particle in the fluid or gas, which can be calculated using the Einstein relation (kinetic theory)
In physics (specifically, the kinetic theory of gases), the Einstein relation is a previously unexpected connection revealed independently by William Sutherland in 1904, Albert Einstein in 1905, and by Marian Smoluchowski in 1906 in their works on ...
.
* ''m'' is the mass of the particle.
* ''F'' is the random force applied to the particle.
* ''t'' is time.
Solving this equation, one obtained the time-dependent diffusion constant in the long-time limit and when the particle is significantly denser than the surrounding fluid,
:
where
* ''k''B is Boltzmann's constant
The Boltzmann constant ( or ) is the proportionality factor that relates the average relative kinetic energy of particles in a gas with the thermodynamic temperature of the gas. It occurs in the definitions of the kelvin and the gas constant, ...
;
* ''T'' is the absolute temperature
Thermodynamic temperature is a quantity defined in thermodynamics as distinct from kinetic theory or statistical mechanics.
Historically, thermodynamic temperature was defined by Kelvin in terms of a macroscopic relation between thermodynamic wor ...
.
* ''μ'' is the mobility of the particle in the fluid or gas, which can be calculated using the Einstein relation (kinetic theory)
In physics (specifically, the kinetic theory of gases), the Einstein relation is a previously unexpected connection revealed independently by William Sutherland in 1904, Albert Einstein in 1905, and by Marian Smoluchowski in 1906 in their works on ...
.
* ''m'' is the mass of the particle.
* ''t'' is time.
Teorell formula for multicomponent diffusion
The Teorell formula with combination of Onsager's definition of the diffusion force gives : where is the mobility of the ''i''th component, is its activity, is the matrix of the coefficients, is the thermodynamic diffusion force, . For the isothermal perfect systems, . Therefore, the Einstein–Teorell approach gives the following multicomponent generalization of the Fick's law for multicomponent diffusion: : where is the matrix of coefficients. The Chapman–Enskog formulas for diffusion in gases include exactly the same terms. Earlier, such terms were introduced in theMaxwell–Stefan diffusion
The Maxwell–Stefan diffusion (or Stefan–Maxwell diffusion) is a model for describing diffusion in multicomponent systems. The equations that describe these transport processes have been developed independently and in parallel by James Clerk Max ...
equation.
Jumps on the surface and in solids
 Diffusion of reagents on the surface of a
Diffusion of reagents on the surface of a catalyst
Catalysis () is the process of increasing the rate of a chemical reaction by adding a substance known as a catalyst (). Catalysts are not consumed in the reaction and remain unchanged after it. If the reaction is rapid and the catalyst recyc ...
may play an important role in heterogeneous catalysis. The model of diffusion in the ideal monolayer is based on the jumps of the reagents on the nearest free places. This model was used for CO on Pt oxidation under low gas pressure.
The system includes several reagents on the surface. Their surface concentrations are The surface is a lattice of the adsorption places. Each
reagent molecule fills a place on the surface. Some of the places are free. The concentration of the free places is . The sum of all (including free places) is constant, the density of adsorption places ''b''.
The jump model gives for the diffusion flux of (''i'' = 1, ..., ''n''):
:
The corresponding diffusion equation is:
:
Due to the conservation law, and we
have the system of ''m'' diffusion equations. For one component we get Fick's law and linear equations because . For two and more components the equations are nonlinear.
If all particles can exchange their positions with their closest neighbours then a simple generalization gives
: