Deformation (geology) on:
[Wikipedia]
[Google]
[Amazon]
In
 Where is constant related to the material flow stress. indicates the derivative of strain by the time, which is also known as strain rate. is the strain-rate sensitivity. Moreover, value of is related to the resistance toward the necking. Usually, the value of is at the range of 0-0.1 at room temperature and as high as 0.8 when the temperature is increased.
By combining the 1) and 2), we can create the ultimate relation as below:
:
Where is the global constant for relating strain, strain rate and stress.
3) Based on the true stress-strain curve and its derivative form, we can estimate the strain necessary to start necking. This can be calculated based on the intersection between true stress-strain curve as shown in right.
This figure also shows the dependency of the necking strain at different temperature. In case of FCC metals, both of the stress-strain curve at its derivative are highly dependent on temperature. Therefore, at higher temperature, necking starts to appear even under lower strain value.
All of these properties indicate the importance of calculating the true stress-strain curve for further analyzing the behavior of materials in sudden environment.
4) A graphical method, so-called "Considere construction", can help determine the behavior of stress-strain curve whether necking or drawing happens on the sample. By setting as determinant, the true stress and strain can be expressed with engineering stress and strain as below:
:
Therefore, the value of engineering stress can be expressed by the secant line from made by true stress and value where to . By analyzing the shape of diagram and secant line, we can determine whether the materials show drawing or necking.
Where is constant related to the material flow stress. indicates the derivative of strain by the time, which is also known as strain rate. is the strain-rate sensitivity. Moreover, value of is related to the resistance toward the necking. Usually, the value of is at the range of 0-0.1 at room temperature and as high as 0.8 when the temperature is increased.
By combining the 1) and 2), we can create the ultimate relation as below:
:
Where is the global constant for relating strain, strain rate and stress.
3) Based on the true stress-strain curve and its derivative form, we can estimate the strain necessary to start necking. This can be calculated based on the intersection between true stress-strain curve as shown in right.
This figure also shows the dependency of the necking strain at different temperature. In case of FCC metals, both of the stress-strain curve at its derivative are highly dependent on temperature. Therefore, at higher temperature, necking starts to appear even under lower strain value.
All of these properties indicate the importance of calculating the true stress-strain curve for further analyzing the behavior of materials in sudden environment.
4) A graphical method, so-called "Considere construction", can help determine the behavior of stress-strain curve whether necking or drawing happens on the sample. By setting as determinant, the true stress and strain can be expressed with engineering stress and strain as below:
:
Therefore, the value of engineering stress can be expressed by the secant line from made by true stress and value where to . By analyzing the shape of diagram and secant line, we can determine whether the materials show drawing or necking.
 On the figure (a), there is only concave upward Considere plot. It indicates that there is no yield drop so the material will be suffered from fracture before it yields. On the figure (b), there is specific point where the tangent matches with secant line at point where . After this value, the slope becomes smaller than the secant line where necking starts to appear. On the figure (c), there is point where yielding starts to appear but when , the drawing happens. After drawing, all the material will stretch and eventually show fracture. Between and , the material itself does not stretch but rather, only the neck starts to stretch out.
On the figure (a), there is only concave upward Considere plot. It indicates that there is no yield drop so the material will be suffered from fracture before it yields. On the figure (b), there is specific point where the tangent matches with secant line at point where . After this value, the slope becomes smaller than the secant line where necking starts to appear. On the figure (c), there is point where yielding starts to appear but when , the drawing happens. After drawing, all the material will stretch and eventually show fracture. Between and , the material itself does not stretch but rather, only the neck starts to stretch out.

engineering
Engineering is the use of scientific method, scientific principles to design and build machines, structures, and other items, including bridges, tunnels, roads, vehicles, and buildings. The discipline of engineering encompasses a broad rang ...
, deformation refers to the change in size or shape of an object. ''Displacements'' are the ''absolute'' change in position of a point on the object. Deflection
Deflection or deflexion may refer to:
Board games
* Deflection (chess), a tactic that forces an opposing chess piece to leave a square
* Khet (game), formerly ''Deflexion'', an Egyptian-themed chess-like game using lasers
Mechanics
* Deflection ...
is the relative change in external displacements on an object. Strain is the ''relative'' internal change in shape of an infinitesimally small cube of material and can be expressed as a non-dimensional change in length or angle of distortion of the cube. Strains are related to the forces acting on the cube, which are known as stress
Stress may refer to:
Science and medicine
* Stress (biology), an organism's response to a stressor such as an environmental condition
* Stress (linguistics), relative emphasis or prominence given to a syllable in a word, or to a word in a phrase ...
, by a stress-strain curve. The relationship between stress and strain is generally linear and reversible up until the yield point
In materials science and engineering, the yield point is the point on a stress-strain curve that indicates the limit of elastic behavior and the beginning of plastic behavior. Below the yield point, a material will deform elastically and wi ...
and the deformation is elastic
Elastic is a word often used to describe or identify certain types of elastomer, elastic used in garments or stretchable fabrics.
Elastic may also refer to:
Alternative name
* Rubber band, ring-shaped band of rubber used to hold objects togeth ...
. The linear relationship for a material is known as Young's modulus
Young's modulus E, the Young modulus, or the modulus of elasticity in tension or compression (i.e., negative tension), is a mechanical property that measures the tensile or compressive stiffness of a solid material when the force is applied leng ...
. Above the yield point, some degree of permanent distortion remains after unloading and is termed plastic deformation
In engineering, deformation refers to the change in size or shape of an object. ''Displacements'' are the ''absolute'' change in position of a point on the object. Deflection is the relative change in external displacements on an object. Strain ...
. The determination of the stress and strain throughout a solid object is given by the field of strength of materials
The field of strength of materials, also called mechanics of materials, typically refers to various methods of calculating the stresses and strains in structural members, such as beams, columns, and shafts. The methods employed to predict the re ...
and for a structure by structural analysis
Structural analysis is a branch of Solid Mechanics which uses simplified models for solids like bars, beams and shells for engineering decision making. Its main objective is to determine the effect of loads on the physical structures and thei ...
.
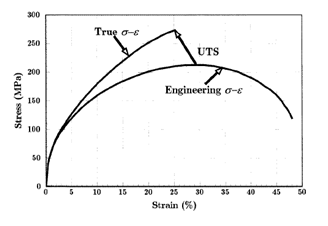
Engineering stress and engineering strain are approximations to the internal state that may be determined from the external forces and deformations of an object, provided that there is no significant change in size. When there is a significant change in size, the true stress and true strain can be derived from the instantaneous size of the object.
In the figure it can be seen that the compressive loading (indicated by the arrow) has caused deformation in the cylinder
A cylinder (from ) has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base.
A cylinder may also be defined as an infin ...
so that the original shape (dashed lines) has changed (deformed) into one with bulging sides. The sides bulge because the material, although strong enough to not crack or otherwise fail, is not strong enough to support the load without change. As a result, the material is forced out laterally. Internal forces (in this case at right angles to the deformation) resist the applied load.
The concept of a rigid body
In physics, a rigid body (also known as a rigid object) is a solid body in which deformation is zero or so small it can be neglected. The distance between any two given points on a rigid body remains constant in time regardless of external force ...
can be applied if the deformation is negligible.
Types of deformation
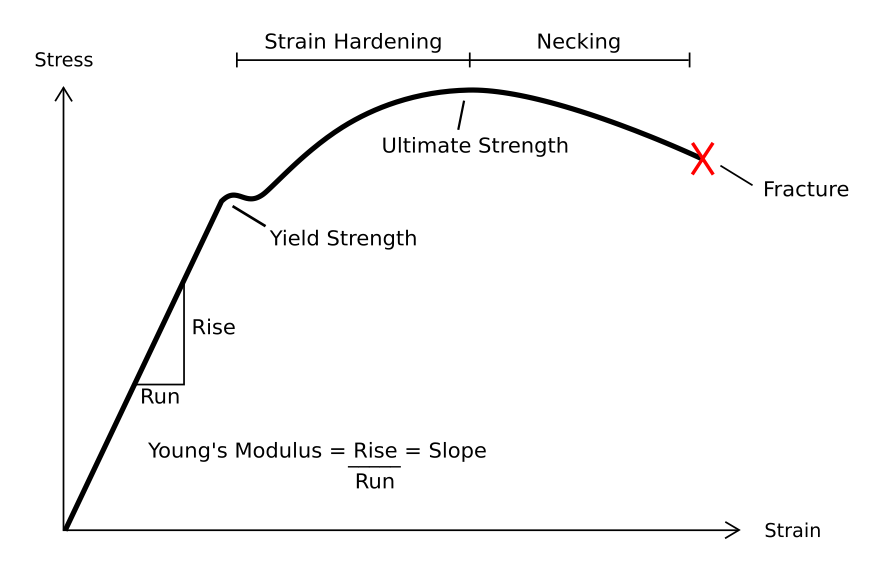
Depending on the type of material, size and geometry of the object, and the forces applied, various types of deformation may result. The image to the right shows the engineering stress vs. strain diagram for a typical ductile material such as steel. Different deformation modes may occur under different conditions, as can be depicted using a deformation mechanism map. Permanent deformation is irreversible; the deformation stays even after removal of the applied forces, while the temporary deformation is recoverable as it disappears after the removal of applied forces. Temporary deformation is also called elastic deformation, while the permanent deformation is called plastic deformation.
Elastic deformation
The study of temporary or elastic deformation in the case of engineering strain is applied to materials used in mechanical and structural engineering, such asconcrete
Concrete is a composite material composed of fine and coarse aggregate bonded together with a fluid cement (cement paste) that hardens (cures) over time. Concrete is the second-most-used substance in the world after water, and is the most wi ...
and steel
Steel is an alloy made up of iron with added carbon to improve its strength and fracture resistance compared to other forms of iron. Many other elements may be present or added. Stainless steels that are corrosion- and oxidation-resistant ty ...
, which are subjected to very small deformations. Engineering strain is modeled by infinitesimal strain theory
In continuum mechanics, the infinitesimal strain theory is a mathematical approach to the description of the deformation of a solid body in which the displacements of the material particles are assumed to be much smaller (indeed, infinitesimally ...
, also called ''small strain theory'', ''small deformation theory'', ''small displacement theory'', or ''small displacement-gradient theory'' where strains and rotations are both small.
For some materials, e.g. elastomers
An elastomer is a polymer with viscoelasticity (i.e. both viscosity and elasticity) and with weak intermolecular forces, generally low Young's modulus and high failure strain compared with other materials. The term, a portmanteau of ''elastic p ...
and polymers, subjected to large deformations, the engineering definition of strain is not applicable, e.g. typical engineering strains greater than 1%, thus other more complex definitions of strain are required, such as ''stretch'', ''logarithmic strain'', ''Green strain'', and ''Almansi strain''. Elastomer
An elastomer is a polymer with viscoelasticity (i.e. both viscosity and elasticity) and with weak intermolecular forces, generally low Young's modulus and high failure strain compared with other materials. The term, a portmanteau of ''elastic p ...
s and shape memory
In metallurgy, a shape-memory alloy (SMA) is an alloy that can be deformed when cold but returns to its pre-deformed ("remembered") shape when heated. It may also be called memory metal, memory alloy, smart metal, smart alloy, or muscle wire.
P ...
metals such as Nitinol
Nickel titanium, also known as Nitinol, is a metal alloy of nickel and titanium, where the two elements are present in roughly equal atomic percentages. Different alloys are named according to the weight percentage of nickel; e.g., Nitinol 55 and ...
exhibit large elastic deformation ranges, as does rubber
Rubber, also called India rubber, latex, Amazonian rubber, ''caucho'', or ''caoutchouc'', as initially produced, consists of polymers of the organic compound isoprene, with minor impurities of other organic compounds. Thailand, Malaysia, and ...
. However, elasticity is nonlinear in these materials.
Normal metals, ceramics and most crystals show linear elasticity and a smaller elastic range.
Linear elastic deformation is governed by Hooke's law
In physics, Hooke's law is an empirical law which states that the force () needed to extend or compress a spring (device), spring by some distance () Proportionality (mathematics)#Direct_proportionality, scales linearly with respect to that ...
, which states:
:
Where is the applied stress
Stress may refer to:
Science and medicine
* Stress (biology), an organism's response to a stressor such as an environmental condition
* Stress (linguistics), relative emphasis or prominence given to a syllable in a word, or to a word in a phrase ...
, is a material constant called Young's modulus
Young's modulus E, the Young modulus, or the modulus of elasticity in tension or compression (i.e., negative tension), is a mechanical property that measures the tensile or compressive stiffness of a solid material when the force is applied leng ...
or elastic modulus
An elastic modulus (also known as modulus of elasticity) is the unit of measurement of an object's or substance's resistance to being deformed elastically (i.e., non-permanently) when a stress is applied to it. The elastic modulus of an object is ...
, and ε is the resulting strain
Strain may refer to:
Science and technology
* Strain (biology), variants of plants, viruses or bacteria; or an inbred animal used for experimental purposes
* Strain (chemistry), a chemical stress of a molecule
* Strain (injury), an injury to a mu ...
. This relationship only applies in the elastic range and indicates that the slope of the stress vs. strain curve can be used to find Young's modulus (). Engineers often use this calculation in tensile tests.
Note that not all elastic materials undergo linear elastic deformation; some, such as concrete
Concrete is a composite material composed of fine and coarse aggregate bonded together with a fluid cement (cement paste) that hardens (cures) over time. Concrete is the second-most-used substance in the world after water, and is the most wi ...
, gray cast iron
Gray iron, or grey cast iron, is a type of cast iron that has a graphitic microstructure. It is named after the gray color of the fracture it forms, which is due to the presence of graphite.. It is the most common cast iron and the most widely u ...
, and many polymers, respond in a nonlinear fashion. For these materials Hooke's law is inapplicable.

True stress and strain
Since we disregard the change of area during deformation above, the true stress and strain curve should be re-derived. For deriving the stress strain curve, we can assume that the volume change is 0 even if we deformed the materials. We can assume that: : Then, the true stress can be expressed as below: : Additionally, the true strain εT can be express as below: : Then, we can express the value as : Thus, we can induce the plot in terms of and as right figure. Additionally, based on the true stress-strain curve, we can estimate the region where necking starts to happen. Since necking starts to appear after ultimate tensile stress where the maximum force applied, we can express this situation as below: : so this form can be expressed as below: : It indicates that the necking starts to appear where reduction of area becomes much significant compared to the stress change. Then the stress will be localized to specific area where the necking appears. Additionally, we can induce various relation based on true stress-strain curve. 1) True strain and stress curve can be expressed by the approximate linear relationship by taking a log on true stress and strain. The relation can be expressed as below: : Where is stress coefficient and is strain-hardening coefficient. Usually, the value of has range around 0.02 to 0.5 at room temperature. If is 1, we can express this material as perfect elastic material. 2) In reality, stress is also highly dependent on the rate of strain variation. Thus, we can induce the empirical equation based on the strain rate variation. : Where is constant related to the material flow stress. indicates the derivative of strain by the time, which is also known as strain rate. is the strain-rate sensitivity. Moreover, value of is related to the resistance toward the necking. Usually, the value of is at the range of 0-0.1 at room temperature and as high as 0.8 when the temperature is increased.
By combining the 1) and 2), we can create the ultimate relation as below:
:
Where is the global constant for relating strain, strain rate and stress.
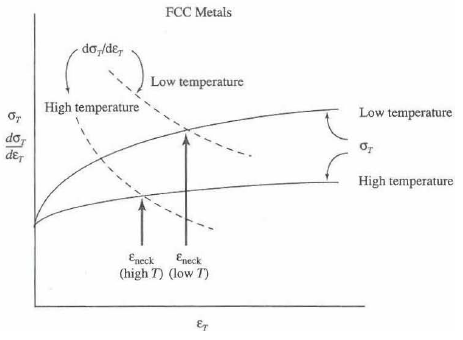
3) Based on the true stress-strain curve and its derivative form, we can estimate the strain necessary to start necking. This can be calculated based on the intersection between true stress-strain curve as shown in right.
This figure also shows the dependency of the necking strain at different temperature. In case of FCC metals, both of the stress-strain curve at its derivative are highly dependent on temperature. Therefore, at higher temperature, necking starts to appear even under lower strain value.
All of these properties indicate the importance of calculating the true stress-strain curve for further analyzing the behavior of materials in sudden environment.
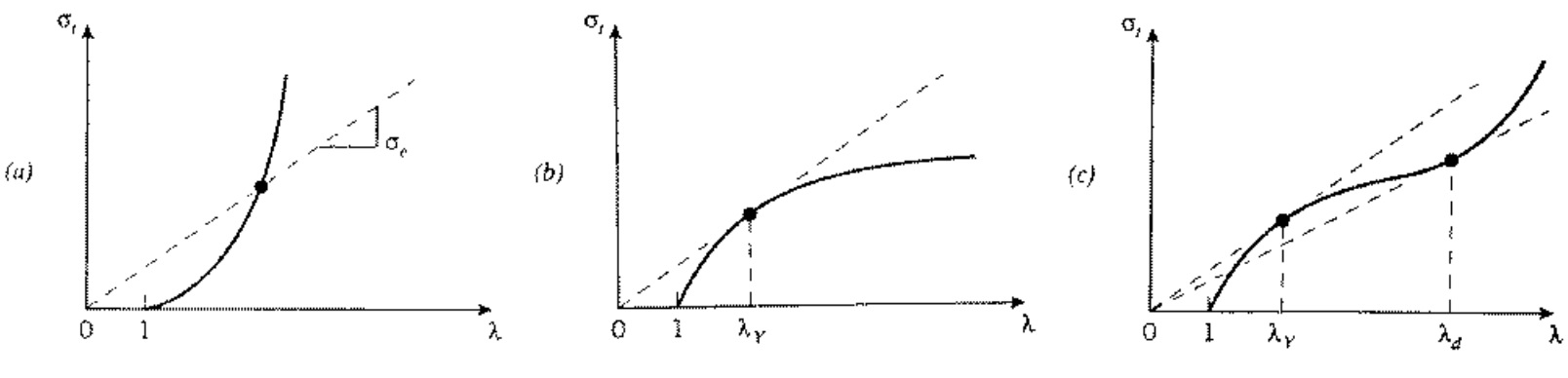
4) A graphical method, so-called "Considere construction", can help determine the behavior of stress-strain curve whether necking or drawing happens on the sample. By setting as determinant, the true stress and strain can be expressed with engineering stress and strain as below:
:
Therefore, the value of engineering stress can be expressed by the secant line from made by true stress and value where to . By analyzing the shape of diagram and secant line, we can determine whether the materials show drawing or necking.
Where is constant related to the material flow stress. indicates the derivative of strain by the time, which is also known as strain rate. is the strain-rate sensitivity. Moreover, value of is related to the resistance toward the necking. Usually, the value of is at the range of 0-0.1 at room temperature and as high as 0.8 when the temperature is increased.
By combining the 1) and 2), we can create the ultimate relation as below:
:
Where is the global constant for relating strain, strain rate and stress.
3) Based on the true stress-strain curve and its derivative form, we can estimate the strain necessary to start necking. This can be calculated based on the intersection between true stress-strain curve as shown in right.
This figure also shows the dependency of the necking strain at different temperature. In case of FCC metals, both of the stress-strain curve at its derivative are highly dependent on temperature. Therefore, at higher temperature, necking starts to appear even under lower strain value.
All of these properties indicate the importance of calculating the true stress-strain curve for further analyzing the behavior of materials in sudden environment.
4) A graphical method, so-called "Considere construction", can help determine the behavior of stress-strain curve whether necking or drawing happens on the sample. By setting as determinant, the true stress and strain can be expressed with engineering stress and strain as below:
:
Therefore, the value of engineering stress can be expressed by the secant line from made by true stress and value where to . By analyzing the shape of diagram and secant line, we can determine whether the materials show drawing or necking.
 On the figure (a), there is only concave upward Considere plot. It indicates that there is no yield drop so the material will be suffered from fracture before it yields. On the figure (b), there is specific point where the tangent matches with secant line at point where . After this value, the slope becomes smaller than the secant line where necking starts to appear. On the figure (c), there is point where yielding starts to appear but when , the drawing happens. After drawing, all the material will stretch and eventually show fracture. Between and , the material itself does not stretch but rather, only the neck starts to stretch out.
On the figure (a), there is only concave upward Considere plot. It indicates that there is no yield drop so the material will be suffered from fracture before it yields. On the figure (b), there is specific point where the tangent matches with secant line at point where . After this value, the slope becomes smaller than the secant line where necking starts to appear. On the figure (c), there is point where yielding starts to appear but when , the drawing happens. After drawing, all the material will stretch and eventually show fracture. Between and , the material itself does not stretch but rather, only the neck starts to stretch out.
Plastic deformation
This type of deformation is not undone simply by removing the applied force. An object in the plastic deformation range, however, will first have undergone elastic deformation, which is undone simply be removing the applied force, so the object will return part way to its original shape. Softthermoplastics
A thermoplastic, or thermosoft plastic, is any plastic polymer material that becomes pliable or moldable at a certain elevated temperature and solidifies upon cooling.
Most thermoplastics have a high molecular weight. The polymer chains associate ...
have a rather large plastic deformation range as do ductile metals such as copper
Copper is a chemical element with the symbol Cu (from la, cuprum) and atomic number 29. It is a soft, malleable, and ductile metal with very high thermal and electrical conductivity. A freshly exposed surface of pure copper has a pinkis ...
, silver
Silver is a chemical element with the Symbol (chemistry), symbol Ag (from the Latin ', derived from the Proto-Indo-European wikt:Reconstruction:Proto-Indo-European/h₂erǵ-, ''h₂erǵ'': "shiny" or "white") and atomic number 47. A soft, whi ...
, and gold
Gold is a chemical element with the symbol Au (from la, aurum) and atomic number 79. This makes it one of the higher atomic number elements that occur naturally. It is a bright, slightly orange-yellow, dense, soft, malleable, and ductile met ...
. Steel
Steel is an alloy made up of iron with added carbon to improve its strength and fracture resistance compared to other forms of iron. Many other elements may be present or added. Stainless steels that are corrosion- and oxidation-resistant ty ...
does, too, but not cast iron
Cast iron is a class of iron–carbon alloys with a carbon content more than 2%. Its usefulness derives from its relatively low melting temperature. The alloy constituents affect its color when fractured: white cast iron has carbide impuriti ...
. Hard thermosetting plastics, rubber, crystals, and ceramics have minimal plastic deformation ranges. An example of a material with a large plastic deformation range is wet chewing gum
Chewing gum is a soft, cohesive substance designed to be chewed without being swallowed. Modern chewing gum is composed of gum base, sweeteners, softeners/plasticizers, flavors, colors, and, typically, a hard or powdered polyol coating. Its te ...
, which can be stretched to dozens of times its original length.
Under tensile stress, plastic deformation is characterized by a strain hardening
In materials science, work hardening, also known as strain hardening, is the strengthening of a metal or polymer by plastic deformation. Work hardening may be desirable, undesirable, or inconsequential, depending on the context.
This strengt ...
region and a necking region and finally, fracture (also called rupture). During strain hardening the material becomes stronger through the movement of atomic dislocations. The necking phase is indicated by a reduction in cross-sectional area of the specimen. Necking begins after the ultimate strength is reached. During necking, the material can no longer withstand the maximum stress and the strain in the specimen rapidly increases. Plastic deformation ends with the fracture of the material.
Compressive failure
Usually, compressive stress applied to bars,column
A column or pillar in architecture and structural engineering is a structural element that transmits, through compression, the weight of the structure above to other structural elements below. In other words, a column is a compression member. ...
s, etc. leads to shortening.
Loading a structural element or specimen will increase the compressive stress until it reaches its compressive strength
In mechanics, compressive strength or compression strength is the capacity of a material or structure to withstand loads tending to reduce size (as opposed to tensile strength which withstands loads tending to elongate). In other words, compre ...
. According to the properties of the material, failure modes are yielding for materials with ductile
Ductility is a mechanical property commonly described as a material's amenability to drawing (e.g. into wire). In materials science, ductility is defined by the degree to which a material can sustain plastic deformation under tensile stres ...
behavior (most metal
A metal (from Greek μέταλλον ''métallon'', "mine, quarry, metal") is a material that, when freshly prepared, polished, or fractured, shows a lustrous appearance, and conducts electricity and heat relatively well. Metals are typicall ...
s, some soil
Soil, also commonly referred to as earth or dirt, is a mixture of organic matter, minerals, gases, liquids, and organisms that together support life. Some scientific definitions distinguish ''dirt'' from ''soil'' by restricting the former te ...
s and plastic
Plastics are a wide range of synthetic or semi-synthetic materials that use polymers as a main ingredient. Their plasticity makes it possible for plastics to be moulded, extruded or pressed into solid objects of various shapes. This adaptab ...
s) or rupturing for brittle behavior (geomaterials, cast iron
Cast iron is a class of iron–carbon alloys with a carbon content more than 2%. Its usefulness derives from its relatively low melting temperature. The alloy constituents affect its color when fractured: white cast iron has carbide impuriti ...
, glass
Glass is a non-crystalline, often transparent, amorphous solid that has widespread practical, technological, and decorative use in, for example, window panes, tableware, and optics. Glass is most often formed by rapid cooling (quenching) of ...
, etc.).
In long, slender structural elements — such as columns or truss
A truss is an assembly of ''members'' such as beams, connected by ''nodes'', that creates a rigid structure.
In engineering, a truss is a structure that "consists of two-force members only, where the members are organized so that the assembl ...
bars — an increase of compressive force ''F'' leads to structural failure
Structural integrity and failure is an aspect of engineering that deals with the ability of a structure to support a designed structural load (weight, force, etc.) without breaking and includes the study of past structural failures in order to ...
due to buckling
In structural engineering, buckling is the sudden change in shape (deformation) of a structural component under load, such as the bowing of a column under compression or the wrinkling of a plate under shear. If a structure is subjected to a gr ...
at lower stress than the compressive strength.
Fracture
This type of deformation is also irreversible. A break occurs after the material has reached the end of the elastic, and then plastic, deformation ranges. At this point forces accumulate until they are sufficient to cause a fracture. All materials will eventually fracture, if sufficient forces are applied.Misconceptions
A popular misconception is that all materials that bend are "weak" and those that don't are "strong". In reality, many materials that undergo large elastic and plastic deformations, such as steel, are able to absorb stresses that would cause brittle materials, such as glass, with minimal plastic deformation ranges, to break.See also
*Artificial cranial deformation
Artificial cranial deformation or modification, head flattening, or head binding is a form of body alteration in which the skull of a human being is deformed intentionally. It is done by distorting the normal growth of a child's skull by applying ...
*Buff strength
Buff strength is a design term used in the certification of passenger railroad cars. It refers to the required resistance to deformation or permanent damage due to loads applied at the car's ends, either from push-or-pull loads on the buffer, Jan ...
*Creep (deformation)
In materials science, creep (sometimes called cold flow) is the tendency of a solid material to move slowly or deform permanently under the influence of persistent mechanical stresses. It can occur as a result of long-term exposure to high leve ...
*Deflection (engineering)
In structural engineering, deflection is the degree to which a part of a structural element is displaced under a load (because it deforms). It may refer to an angle or a distance.
The deflection distance of a member under a load can be calcula ...
*Deformation (mechanics)
In physics, deformation is the continuum mechanics transformation of a body from a ''reference'' configuration to a ''current'' configuration. A configuration is a set containing the positions of all particles of the body.
A deformation can ...
*Deformation mechanism maps
A deformation mechanism, in geology, is a process occurring at a microscopic scale that is responsible for changes in a material's internal structure, shape and volume. The process involves planar Discontinuity (geotechnical engineering), discontin ...
*Deformation monitoring
Deformation monitoring (also referred to as deformation survey) is the systematic measurement and tracking of the alteration in the shape or dimensions of an object as a result of stresses induced by applied loads. Deformation monitoring is a major ...
*Deformation retract
In topology, a branch of mathematics, a retraction is a continuous mapping from a topological space into a subspace that preserves the position of all points in that subspace. The subspace is then called a retract of the original space. A deforma ...
*Deformation theory
In mathematics, deformation theory is the study of infinitesimal conditions associated with varying a solution ''P'' of a problem to slightly different solutions ''P''ε, where ε is a small number, or a vector of small quantities. The infinitesim ...
*Elasticity
Elasticity often refers to:
*Elasticity (physics), continuum mechanics of bodies that deform reversibly under stress
Elasticity may also refer to:
Information technology
* Elasticity (data store), the flexibility of the data model and the cl ...
*Malleability
Ductility is a List of materials properties, mechanical property commonly described as a material's amenability to Drawing (manufacturing), drawing (e.g. into wire). In materials science, ductility is defined by the degree to which a materia ...
*Planar deformation features
Planar deformation features, or PDFs, are optically recognizable microscopic features in grains of silicate minerals (usually quartz or feldspar), consisting of very narrow planes of glassy material arranged in parallel sets that have distinct orie ...
*Plasticity (physics)
In physics and materials science, plasticity, also known as plastic deformation, is the ability of a solid material to undergo permanent Deformation (engineering), deformation, a non-reversible change of shape in response to applied forces. F ...
*Poisson's ratio
In materials science and solid mechanics, Poisson's ratio \nu ( nu) is a measure of the Poisson effect, the deformation (expansion or contraction) of a material in directions perpendicular to the specific direction of loading. The value of Pois ...
*Strain tensor
In continuum mechanics, the infinitesimal strain theory is a mathematical approach to the description of the deformation of a solid body in which the displacements of the material particles are assumed to be much smaller (indeed, infinitesimally ...
*Strength of materials
The field of strength of materials, also called mechanics of materials, typically refers to various methods of calculating the stresses and strains in structural members, such as beams, columns, and shafts. The methods employed to predict the re ...
*Wood warping
Wood warping is a deviation from flatness in timber as a result of stresses and uneven shrinkage. Warping can also occur in wood considered "dry" (wood can take up and release moisture indefinitely), when it takes up moisture unevenly, or – es ...
References
{{DEFAULTSORT:Deformation (Engineering) Solid mechanics Deformation (mechanics)