Collatz conjecture

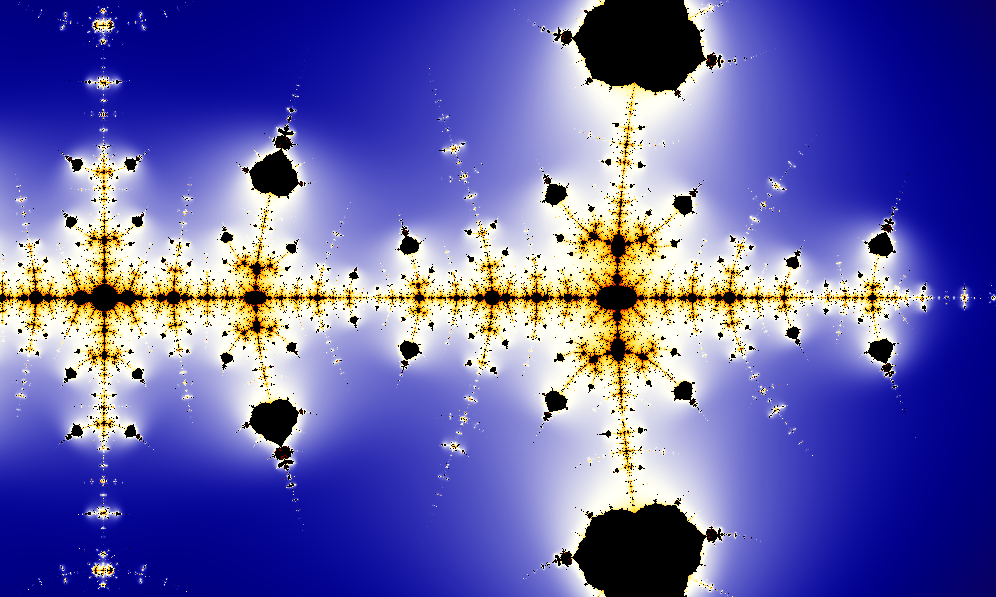The Collatz conjecture is one of the most famous unsolved problems in mathematics. The conjecture asks whether repeating two simple arithmetic operations will eventually transform every positive integer into 1. It concerns sequences of integers in which each term is obtained from the previous term as follows: if the previous term is even, the next term is one half of the previous term. If the previous term is odd, the next term is 3 times the previous term plus 1. The conjecture is that these sequences always reach 1, no matter which positive integer is chosen to start the sequence.

It is named after mathematician Lothar Collatz, who introduced the idea in 1937, two years after receiving his doctorate. It is also known as the problem, the conjecture, the Ulam conjecture (after Stanisław Ulam), Kakutani's problem (after Shizuo Kakutani), the Thwaites conjecture (after Sir Bryan Thwaites), Hasse's algorithm (after Helmut Hasse), or the Syracuse problem.
The sequence of numbers involved is sometimes referred to as the hailstone sequence, hailstone numbers or hailstone numerals (because the values are usually subject to multiple descents and ascents like hailstones in a cloud), or as wondrous numbers.

Paul Erdős said about the Collatz conjecture: "Mathematics may not be ready for such problems." He also offered US$500 for its solution. Jeffrey Lagarias stated in 2010 that the Collatz conjecture "is an extraordinarily difficult problem, completely out of reach of present day mathematics".

Statement of the problem

Consider the following operation on an arbitrary positive integer:

* If the number is even, divide it by two.
* If the number is odd, triple it and add one.

In modular arithmetic notation, define the function as follows:
f(n) = \begin \frac &\text n \equiv 0 \pmod\\ px3n+1 & \text n\equiv 1 \pmod .\end

Now form a sequence by performing this operation repeatedly, beginning with any positive integer, and taking the result at each step as the input at the next.

In notation:
$a_i = \beginn & \text i = 0 \\ f(a_) & \text i > 0 \end$
(that is: is the value of applied to recursively times; ).

The Collatz conjecture is: ''This process will eventually reach the number 1, regardless of which positive integer is chosen initially.''

If the conjecture is false, it can only be because there is some starting number which gives rise to a sequence that does not contain 1. Such a sequence would either enter a repeating cycle that excludes 1, or increase without bound. No such sequence has been found.

The smallest such that is called the stopping time of . Similarly, the smallest such that is called the total stopping time of . If one of the indexes or doesn't exist, we say that the stopping time or the total stopping time, respectively, is infinite.

The Collatz conjecture asserts that the total stopping time of every is finite. It is also equivalent to saying that every has a finite stopping time.

Since is even whenever is odd, one may instead use the "shortcut" form of the Collatz function:
f(n) = \begin \frac &\text n \equiv 0 \pmod,\\ px\frac & \text n\equiv 1 \pmod. \end
This definition yields smaller values for the stopping time and total stopping time without changing the overall dynamics of the process.

Empirical data

For instance, starting with and applying the function without "shortcut", one gets the sequence 12, 6, 3, 10, 5, 16, 8, 4, 2, 1.

The number takes longer to reach 1: 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1.

The sequence for , listed and graphed below, takes 111 steps (41 steps through odd numbers, in bold), climbing as high as 9232 before descending to 1.

: 27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1

Numbers with a total stopping time longer than that of any smaller starting value form a sequence beginning with:
:1, 2, 3, 6, 7, 9, 18, 25, 27, 54, 73, 97, 129, 171, 231, 313, 327, 649, 703, 871, 1161, 2223, 2463, 2919, 3711, 6171, ... .

The starting values whose maximum trajectory point is greater than that of any smaller starting value are as follows:
:1, 2, 3, 7, 15, 27, 255, 447, 639, 703, 1819, 4255, 4591, 9663, 20895, 26623, 31911, 60975, 77671, 113383, 138367, 159487, 270271, 665215, 704511, ...

Number of steps for to reach 1 are
:0, 1, 7, 2, 5, 8, 16, 3, 19, 6, 14, 9, 9, 17, 17, 4, 12, 20, 20, 7, 7, 15, 15, 10, 23, 10, 111, 18, 18, 18, 106, 5, 26, 13, 13, 21, 21, 21, 34, 8, 109, 8, 29, 16, 16, 16, 104, 11, 24, 24, ...

The starting value having the largest total stopping time while being
:less than 10 is 9, which has 19 steps,
:less than 100 is 97, which has 118 steps,
:less than 1000 is 871, which has 178 steps,
:less than 10⁴ is 6171, which has 261 steps,
:less than 10⁵ is , which has 350 steps,
:less than 10⁶ is , which has 524 steps,
:less than 10⁷ is , which has 685 steps,
:less than 10⁸ is , which has 949 steps,
:less than 10⁹ is , which has 986 steps,
:less than 10¹⁰ is , which has 1132 steps,
:less than 10¹¹ is , which has 1228 steps,
:less than 10¹² is , which has 1348 steps. (Note: "Delay records" are total stopping time records.)

These numbers are the lowest ones with the indicated step count, but not necessarily the only ones below the given limit. As an example, has 1132 steps, as does .

The starting values having the smallest total stopping time with respect to their number of digits (in base 2) are the powers of two since is halved times to reach 1, and is never increased.

Visualizations

File:Collatz orbits of the all integers up to 1000.svg, Directed graph showing the orbits of the first 1000 numbers.
File:CollatzConjectureGraphMaxValues.jpg, The axis represents starting number, the axis represents the highest number reached during the chain to 1. This plot shows a restricted axis: some values produce intermediates as high as (for )
File:Collatz-max.png, The same plot on the left but on log scale, so all values are shown. The first thick line towards the middle of the plot corresponds to the tip at 27, which reaches a maximum at 4616.
File:All Collatz sequences of a length inferior to 20.svg, The tree of all the numbers having fewer than 20 steps.
File:Collatz Conjecture 100M.jpg, alt=Collatz Conjecture 100M, The number of iterations it takes to get to one for the first 100 million numbers.

Supporting arguments

Although the conjecture has not been proven, most mathematicians who have looked into the problem think the conjecture is true because experimental evidence and heuristic arguments support it.

Experimental evidence

, the conjecture has been checked by computer for all starting values up to 2⁶⁸ ≈ . All initial values tested so far eventually end in the repeating cycle of period 3.

This computer evidence is not sufficient to prove that the conjecture is true for all starting values. As in the case of some disproved conjectures, like the Pólya conjecture, counterexamples might be found when considering very large numbers.

However, such verifications may have other implications. For example, one can derive additional constraints on the period and structural form of a non-trivial cycle.

A probabilistic heuristic

If one considers only the ''odd'' numbers in the sequence generated by the Collatz process, then each odd number is on average of the previous one. (More precisely, the geometric mean of the ratios of outcomes is .) This yields a heuristic argument that every Hailstone sequence should decrease in the long run, although this is not evidence against other cycles, only against divergence. The argument is not a proof because it assumes that Hailstone sequences are assembled from uncorrelated probabilistic events. (It does rigorously establish that the 2-adic extension of the Collatz process has two division steps for every multiplication step for almost all 2-adic starting values.)

Stopping times

As proven by Riho Terras, almost every positive integer has a finite stopping time. In other words, almost every Collatz sequence reaches a point that is strictly below its initial value. The proof is based on the distribution of parity vectors and uses the central limit theorem.

In 2019, Terence Tao improved this result by showing, using logarithmic density, that almost all Collatz orbits are descending below any given function of the starting point, provided that this function diverges to infinity, no matter how slowly. Responding to this work, '' Quanta Magazine'' wrote that Tao "came away with one of the most significant results on the Collatz conjecture in decades".

Lower bounds

In a computer-aided proof, Krasikov and Lagarias showed that the number of integers in the interval that eventually reach 1 is at least equal to for all sufficiently large .

Cycles

In this part, consider the shortcut form of the Collatz function
f(n) = \begin \frac &\text n \equiv 0 \pmod,\\ px\frac & \text n \equiv 1 \pmod. \end
A cycle is a sequence of distinct positive integers where , , ..., and .

The only known cycle is of period 2, called the trivial cycle.

Cycle length

The length of a non-trivial cycle is known to be at least . In fact, Eliahou (1993) proved that the period of any non-trivial cycle is of the form
$p = 301994 a + 17087915 b + 85137581 c$
where , and are non-negative integers, and . This result is based on the continued fraction expansion of .

-cycles

A -cycle is a cycle that can be partitioned into contiguous subsequences: increasing sequences of odd numbers alternating with decreasing sequences of even numbers. For instance, if the cycle consists of a single increasing sequence of odd numbers followed by a decreasing sequence of even numbers, it is called a ''1-cycle''.

Steiner (1977) proved that there is no 1-cycle other than the trivial . Simons (2005) used Steiner's method to prove that there is no 2-cycle. Simons & de Weger (2005) extended this proof up to 68-cycles: there is no -cycle up to . For each beyond 68, this method gives an upper bound for the smallest term of a -cycle: for example, if there is a 77-cycle, then at least one element of the cycle is less than . Along with the verification of the conjecture up to , this implies the nonexistence of a non-trivial -cycle up to . As exhaustive computer searches continue, larger values may be ruled out. To state the argument more intuitively: we need not look for cycles that have at most 77 circuits, where each circuit consists of consecutive ups followed by consecutive downs.

Other formulations of the conjecture

In reverse

There is another approach to prove the conjecture, which considers the bottom-up
method of growing the so-called ''Collatz graph''. The ''Collatz graph'' is a graph defined by the inverse relation
R(n) = \begin \ & \text n\equiv 0,1,2,3,5 \\ px\left\ & \text n\equiv 4 \end \pmod 6.

So, instead of proving that all positive integers eventually lead to 1, we can try to prove that 1 leads backwards to all positive integers. For any integer , if and only if . Equivalently, if and only if . Conjecturally, this inverse relation forms a tree except for the 1–2–4 loop (the inverse of the 4–2–1 loop of the unaltered function defined in the Statement of the problem section of this article).

When the relation of the function is replaced by the common substitute "shortcut" relation , the Collatz graph is defined by the inverse relation,
R(n) = \begin \ & \text n\equiv 0,1 \\ px\left\ & \text n\equiv 2 \end \pmod 3.

For any integer , if and only if . Equivalently, if and only if . Conjecturally, this inverse relation forms a tree except for a 1–2 loop (the inverse of the 1–2 loop of the function f(n) revised as indicated above).

Alternatively, replace the with where and is the highest power of 2 that divides (with no remainder). The resulting function maps from odd numbers to odd numbers. Now suppose that for some odd number , applying this operation times yields the number 1 (that is, ). Then in binary, the number can be written as the concatenation of strings where each is a finite and contiguous extract from the representation of . The representation of therefore holds the repetends of , where each repetend is optionally rotated and then replicated up to a finite number of bits. It is only in binary that this occurs. Conjecturally, every binary string that ends with a '1' can be reached by a representation of this form (where we may add or delete leading '0's to ).

As an abstract machine that computes in base two

Repeated applications of the Collatz function can be represented as an abstract machine that handles strings of bits. The machine will perform the following three steps on any odd number until only one remains:

# Append to the (right) end of the number in binary (giving );
# Add this to the original number by binary addition (giving );
# Remove all trailing s (that is, repeatedly divide by 2 until the result is odd).

Example

The starting number 7 is written in base two as . The resulting Collatz sequence is:

111
1111
10110
10111
100010
100011
110100
11011
101000
1011
10000

As a parity sequence

For this section, consider the Collatz function in the slightly modified form
f(n) = \begin \frac &\text n \equiv 0 \\ px\frac & \text n \equiv 1 \end \pmod.

This can be done because when is odd, is always even.

If is the parity of a number, that is and , then we can define the Collatz parity sequence (or parity vector) for a number as , where , and .

Which operation is performed, or , depends on the parity. The parity sequence is the same as the sequence of operations.

Using this form for , it can be shown that the parity sequences for two numbers and will agree in the first terms if and only if and are equivalent modulo . This implies that every number is uniquely identified by its parity sequence, and moreover that if there are multiple Hailstone cycles, then their corresponding parity cycles must be different.

Applying the function times to the number will give the result , where is the result of applying the function times to , and is how many increases were encountered during that sequence. For example, for there are 3 increases as 1 iterates to 2, 1, 2, 1, and finally to 2 so the result is ; for there is only 1 increase as 1 rises to 2 and falls to 1 so the result is . When is then there will be rises and the result will be . The factor of 3 multiplying is independent of the value of ; it depends only on the behavior of . This allows one to predict that certain forms of numbers will always lead to a smaller number after a certain number of iterations: for example, becomes after two applications of and becomes after 4 applications of . Whether those smaller numbers continue to 1, however, depends on the value of .

As a tag system

For the Collatz function in the form

f(n) = \begin \frac &\text n \equiv 0 \\ px\frac & \text n \equiv 1. \end \pmod

Hailstone sequences can be computed by the 2-tag system with production rules

:, , .

In this system, the positive integer is represented by a string of copies of , and iteration of the tag operation halts on any word of length less than 2. (Adapted from De Mol.)

The Collatz conjecture equivalently states that this tag system, with an arbitrary finite string of as the initial word, eventually halts (see '' Tag system'' for a worked example).

Extensions to larger domains

Iterating on all integers

An extension to the Collatz conjecture is to include all integers, not just positive integers. Leaving aside the cycle 0 → 0 which cannot be entered from outside, there are a total of four known cycles, which all nonzero integers seem to eventually fall into under iteration of . These cycles are listed here, starting with the well-known cycle for positive :

Odd values are listed in large bold. Each cycle is listed with its member of least absolute value (which is always odd) first.

The generalized Collatz conjecture is the assertion that every integer, under iteration by , eventually falls into one of the four cycles above or the cycle 0 → 0. (The 0 → 0 cycle is only included for the sake of completeness.)

Iterating on rationals with odd denominators

The Collatz map can be extended to (positive or negative) rational numbers which have odd denominators when written in lowest terms.
The number is taken to be 'odd' or 'even' according to whether its numerator is odd or even. Then the formula for the map is exactly the same as when the domain is the integers: an 'even' such rational is divided by 2; an 'odd' such rational is multiplied by 3 and then 1 is added. A closely related fact is that the Collatz map extends to the ring of 2-adic integers, which contains the ring of rationals with odd denominators as a subring.

When using the "shortcut" definition of the Collatz map, it is known that any periodic parity sequence is generated by exactly one rational. Conversely, it is conjectured that every rational with an odd denominator has an eventually cyclic parity sequence (Periodicity Conjecture).

If a parity cycle has length and includes odd numbers exactly times at indices , then the unique rational which generates immediately and periodically this parity cycle is

For example, the parity cycle has length 7 and four odd terms at indices 0, 2, 3, and 6. It is repeatedly generated by the fraction
$\frac = \frac$
as the latter leads to the rational cycle
$\frac \rightarrow \frac \rightarrow \frac \rightarrow \frac \rightarrow \frac \rightarrow \frac \rightarrow \frac \rightarrow \frac .$

Any cyclic permutation of is associated to one of the above fractions. For instance, the cycle is produced by the fraction
$\frac = \frac .$

For a one-to-one correspondence, a parity cycle should be ''irreducible'', that is, not partitionable into identical sub-cycles. As an illustration of this, the parity cycle and its sub-cycle are associated to the same fraction when reduced to lowest terms.

In this context, assuming the validity of the Collatz conjecture implies that and are the only parity cycles generated by positive whole numbers (1 and 2, respectively).

If the odd denominator of a rational is not a multiple of 3, then all the iterates have the same denominator and the sequence of numerators can be obtained by applying the " " generalization of the Collatz function
T_d(x) = \begin
\frac &\text x \equiv 0 \pmod,\\ px \frac & \text x\equiv 1 \pmod.
\end

2-adic extension

The function
T(x) = \begin \frac &\text x \equiv 0 \pmod\\ px\frac & \text x\equiv 1 \pmod \end
is well-defined on the ring $\mathbb_2$ of 2-adic integers, where it is continuous and measure-preserving with respect to the 2-adic measure. Moreover, its dynamics is known to be ergodic.

Define the ''parity vector'' function acting on $\mathbb_2$ as
$Q(x) = \sum_^ \left( T^k (x) \mod 2 \right) 2^k .$

The function is a 2-adic isometry. Consequently, every infinite parity sequence occurs for exactly one 2-adic integer, so that almost all trajectories are acyclic in $\mathbb_2$.

An equivalent formulation of the Collatz conjecture is that
$Q\left(\mathbb^\right) \subset \tfrac13 \mathbb.$

Iterating on real or complex numbers

The Collatz map (with shortcut) can be viewed as the restriction to the integers of the smooth map
$f(z)=\frac z \cos^2\left(\frac z\right)+\frac \sin^2\left(\frac z\right).$

The iterations of this map on the real line lead to a dynamical system, further investigated by Chamberland.
He showed that the conjecture does not hold for positive real numbers since there are infinitely many fixed points, as well as orbits escaping monotonically to infinity. The function has two attracting cycles of period 2, and . Moreover, the set of unbounded orbits is conjectured to be of measure 0.

Letherman, Schleicher, and Wood extended the study to the complex plane, where most of the points have orbits that diverge to infinity (colored region on the illustration). The boundary between the colored region and the black components, namely the Julia set of , is a fractal pattern, sometimes called the "Collatz fractal".

Optimizations

Time–space tradeoff

The section '' As a parity sequence'' above gives a way to speed up simulation of the sequence. To jump ahead steps on each iteration (using the function from that section), break up the current number into two parts, (the least significant bits, interpreted as an integer), and (the rest of the bits as an integer). The result of jumping ahead is given by
:.
The values of (or better ) and can be precalculated for all possible -bit numbers , where is the result of applying the function times to , and is the number of odd numbers encountered on the way. For example, if , one can jump ahead 5 steps on each iteration by separating out the 5 least significant bits of a number and using

: (0...31, 5) = ,
: (0...31, 5) = .

This requires precomputation and storage to speed up the resulting calculation by a factor of , a space–time tradeoff.

Modular restrictions

For the special purpose of searching for a counterexample to the Collatz conjecture, this precomputation leads to an even more important acceleration, used by Tomás Oliveira e Silva in his computational confirmations of the Collatz conjecture up to large values of . If, for some given and , the inequality

:

holds for all , then the first counterexample, if it exists, cannot be modulo . For instance, the first counterexample must be odd because , smaller than ; and it must be 3 mod 4 because , smaller than . For each starting value which is not a counterexample to the Collatz conjecture, there is a for which such an inequality holds, so checking the Collatz conjecture for one starting value is as good as checking an entire congruence class. As increases, the search only needs to check those residues that are not eliminated by lower values of . Only an exponentially small fraction of the residues survive. For example, the only surviving residues mod 32 are 7, 15, 27, and 31.

Syracuse function

If is an odd integer, then is even, so with odd and . The Syracuse function is the function from the set of odd integers into itself, for which .

Some properties of the Syracuse function are:

* For all , . (Because .)
* In more generality: For all and odd , . (Here is function iteration notation.)
* For all odd ,

The Collatz conjecture is equivalent to the statement that, for all in , there exists an integer such that .

Undecidable generalizations

In 1972, John Horton Conway proved that a natural generalization of the Collatz problem is algorithmically undecidable.

Specifically, he considered functions of the form
$\;\;, \text \;$
and are rational numbers which are so chosen that is always an integer.

The standard Collatz function is given by , , , , . Conway proved that the problem:

: Given and , does the sequence of iterates reach 1?

is undecidable, by representing the halting problem in this way.

Closer to the Collatz problem is the following ''universally quantified'' problem:

: Given does the sequence of iterates reach 1, for all ?

Modifying the condition in this way can make a problem either harder or easier to solve (intuitively, it is harder to justify a positive answer but might be easier to justify a negative one). Kurtz and Simon A
PDF
/ref> proved that the above problem is, in fact, undecidable and even higher in the arithmetical hierarchy, specifically -complete. This hardness result holds even if one restricts the class of functions by fixing the modulus to 6480.

In popular culture

In the movie ''Incendies'', a graduate student in pure mathematics explains the Collatz conjecture to a group of undergraduates. She puts her studies on hold for a time to address some unresolved questions about her family's past. Late in the movie, the Collatz conjecture turns out to have foreshadowed a disturbing and difficult discovery that she makes about her family.

See also

* semigroup
* Arithmetic dynamics
* Modular arithmetic
* Residue-class-wise affine group

Further reading

:* ''The Ultimate Challenge: The Problem'', published in 2010 by the American Mathematical Society and edited by Jeffrey Lagarias, is a compendium of information on the Collatz conjecture, methods of approaching it, and generalizations. It includes two survey papers by the editor and five by other authors concerning the history of the problem, generalizations, statistical approaches, and results from the theory of computation. It also includes reprints of early papers on the subject, including the paper by Lothar Collatz.

References

External links

*
* An ongoing volunteer computingbr>project
by David Bařina verifies Convergence of the Collatz conjecture for large values. (furthest progress so far)
* (BOINC) volunteer computin
project
that verifies the Collatz conjecture for larger values.
* An ongoing volunteer computin

by Eric Roosendaal verifies the Collatz conjecture for larger and larger values.
* Another ongoing volunteer computin

by Tomás Oliveira e Silva continues to verify the Collatz conjecture (with fewer statistics than Eric Roosendaal's page but with further progress made).
*
* .
*
*
*
* {{cite AV media , medium=short video , people={{ill, Alex Kontorovich, de (featuring) , title=The simplest math problem no one can solve , date=30 July 2021 , series=Veritasium , via=YouTube , url=https://www.youtube.com/watch?v=094y1Z2wpJg

Are computers ready to solve this notoriously unwieldy math problem?

Conjectures
Arithmetic dynamics
Integer sequences
Unsolved problems in number theory