Capillary bridges on:
[Wikipedia]
[Google]
[Amazon]
Usually, we understand the term capillary bridge as a minimized surface of liquid or 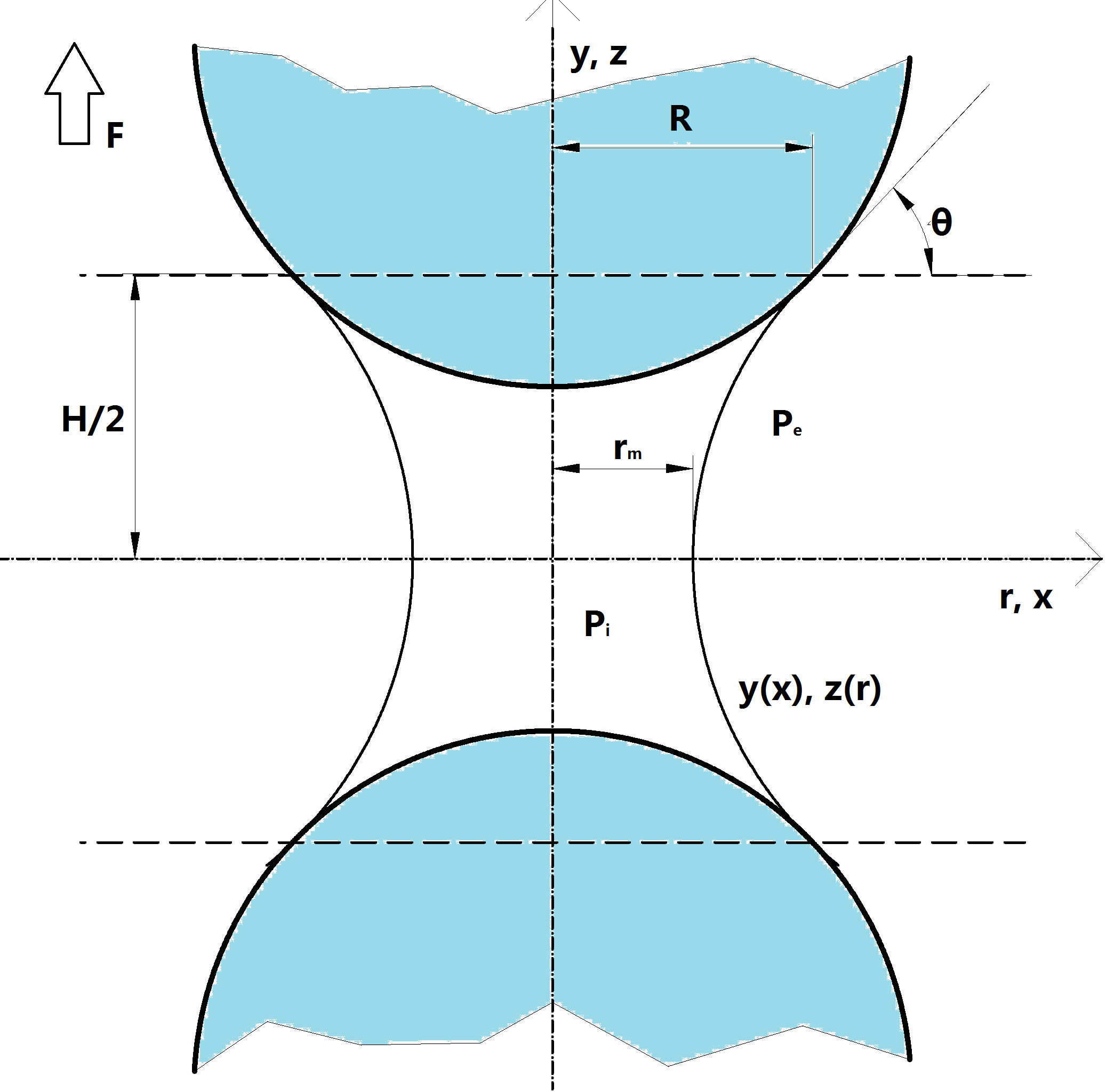 Capillary bridges and their properties may also be influenced by Earth gravity and by properties of the bridged surfaces. The bridging substance may be a liquid or a gas. The enclosing boundary is called the interface (
Capillary bridges and their properties may also be influenced by Earth gravity and by properties of the bridged surfaces. The bridging substance may be a liquid or a gas. The enclosing boundary is called the interface (
Many scientists contributed to the solution of the problem. One of them is Thomas Young. Pierre Simon Laplace contributed the notion of capillary tension. Laplace even formulated the widely known nowadays condition for mechanical equilibrium between two fluids, divided by a capillary surface ''P''γ=Δ''P'' i.e. capillary pressure between two phases is balanced by their adjacent pressure difference.
A general survey on capillary bridge behavior in gravity field is completed by Myshkis and Babskii.A.D. Myshkis and V.G. Babskii, Low-Gravity Fluid Mechanics: Mathematical Theory of Capillary Phenomena, Springer-Verlag 1987
In the last century a lot of efforts were put of study of surface forces that drive capillary effects of bridging. There was established that these forces result from intermolecular forces and become significant in thin fluid gaps (<10 nm) between two surfaces.
The instability of capillary bridges was discussed in first time by Rayleigh.Strut, J. W., Lord Rayleigh, On the instability of jets, Proceedings of London Mathematical Society, v.10, pp. 4-13 (1878) He demonstrated that a liquid jet or capillary cylindrical surface became unstable when the ratio between its length, ''H'' to the radius ''R'', becomes bigger than 2π. In these conditions of small sinusoidal perturbations with wavelength bigger than its perimeter, the cylinder surface area becomes larger than the one of unperturbed cylinder with the same volume and thus it becomes unstable. Later, Hove formulated the variational requirements for the stability of axisymmetric capillary surfaces (unbounded) in absence of gravity and with disturbances constrained to constant volume. He first solved Young-Laplace equation for equilibrium shapes and showed that the Legendre condition for the second variation is always satisfied. Therefore, the stability is determined by the absence of negative eigenvalue of the linearized Young-Laplace equation. This approach of determining stability from second variation is used now widely. Perturbation methods became very successful despite that nonlinear nature of capillary interaction can limit their application. Other methods now include direct simulation. To that moment most methods for stability determination required calculation of equilibrium as a basis for perturbations. There appeared a new idea that stability may be deduced from equilibrium states. The proposition was further proven by Pitts for axisymmetric constant volume. In the following years Vogel extended the theory. He examined the case of axisymmetric capillary bridges with constant volumes and the stability changes correspond to turning points. The recent development of bifurcation theory proved that ''exchange of stability'' between turning points and branch points is a general phenomenon.
Colosse-djéhoutihétep2.jpg, Schematic from the tomb of
Capillary bridges also widely spread in living nature. Bugs, flies, grasshoppers and tree frogs are capable to adhere to vertical rough surfaces because of their ability to inject wetting liquid into the pad-substrate contact area. This way is created long range attractive interaction due to the formation of capillary bridges. Many medical problems involving respiratory diseases, and the health of the body joints depend on tiny capillary bridges. Liquid bridges are now commonly used in growth of cell cultures because of the need to mimic work of living tissues in scientific research.
Let's assume the following cylindrical coordinate system: ''z'' shows axis of revolution; ''r'' represents radial coordinate and ''φ'' is the angle between the normal and the positive ''z'' axis. The nodoid has vertical tangents at ''r'' = ''r''1 and ''r'' = ''r''2 and horizontal tangent at ''r'' = ''r''3. When ''φ'' is the angle between the normal to the interface and positive ''z'' axis then ''φ'' is equal to 90°, 0°, -90° for nodoid.
The Young-Laplace equation may be written in a form convenient for integration for axial symmetry : where ''R''1, ''R''2 are the radii of curvature and ''γ'' is interfacial surface tension.
The integration of the equation is called ''the first integral'' and it yields: Since:
One finds: After the integration, the obtained equation is called ''the second integral'':
where: F and E are
''The second integral'' for unduloid is obtained: where the relation between parameters k and φ are defined the same way as above. In the limiting case ''r''1=0, both nodoid and unduloid consist of a series of spheres. When ''r''1=''r''2. The last and the very interesting limiting case is ''catenoid''. The Laplace equation is reduced to:
It integration can be represented in very convenient form, in cylindrical coordinate system, called ''catenary equation'':
Equation (9) is important because it shows in some simplification all issues, related to the capillary bridges, transparent. Drawing in dimensionless coordinates exhibit a maximum, that distinguishes two branches. One of them is energetically favorable and come up to existence in statics while the other (in dashed line) is not energetically favorable. Maximum is important because when stretching quasi-equilibrium way capillary bridge, if maximum is reached, it breakage takes place. Catenoids with energetically unfavorable dimensions may form during process of dynamical stretching/pressing. Zero capillary pressure ''C''=0 is natural for classical catenoid (capillary soap surface stretched between two coaxial rings). When typical capillary bridge comes to catenoidal state of ''C'' = 0, despite that it surface properties are the same as classical catenoid, it is more appropriate to be presented as scaled by cube root of its volume rather than the radius, ''R''. The solution of ''the second integral'' is different in cases of oblate capillary bridges (nodoid and unduloid): where: F and E are again elliptic integrals of first and second kind, and φ is related to r according to: .
It is important to note that all described curves are found by rolling a conic section without slip along ''z'' axis. The unduloid is described by the focus of rolling ellipse, which can degenerate into a line, a sphere or a parabola, leading to the corresponding limiting cases. Similarly, a nodoid is described by the focus of a rolling hyperbola.
Well systematized summary of capillary bridges shapes is given in table 11.1 of Kralchevsky and Nagayama's book.
The first integral is easily obtained regarding dimensionless capillary pressure at the contact with surface:
where , dimensionless radius at the contact is and ''θ'' is the contact angle. The relation shows that capillary pressure can be positive or negative. The shape of capillary bridges is governed by the equation:
where the equation is obtained after substitution is made in Eq. () and scalling is introduced.
Upon integration, the equation yields: The dimensionless circular radii 1/2C coincides with capillary bridge radii of curvature. The positive sign '+' represents generatrix profile of concave bridge and negative '-', oblate. For the convex capillary bridges, the circular generatrix is retained until the boundary of definition domain is reached while stretching. Near the beginning of self-initiated breakage kinetics, the bridge profile evolves consequently to an ellipse, parabola and possibly to hyperbola.
After the integration, for the capillary bridge height is obtained Similar way for contact radius ''R'', is obtained the integrated equation where and In fig. 6 are shown number of stable static states of liquid capillary bridge, represented by two characteristic parameters: (i) dimensionless height that is obtained by scaling of capillary bridge height by cubic root of its volume Eq. () and (ii) its radius, also scaled by cubic root of volume, Eq. (). The partially analytical solutions, obtained for these two parameters, are presented above. The solutions somehow differs from widely accepted Plateau's approach y elliptical functions, Eq. () because they offer convenient numerical approach for integration of regular integrals, while irregular part of the equation was integrated analytically. These solutions became further a basis for prediction of capillary bridges quasi-equilibrium stretching and breakage for contact angles below 45°. The practical implementation allows to be identified not only the end of definition domain but also the exact behavior during the capillary bridge stretching, because in coordinates stretching forms an inclined line, where the inclination angle is proportional to the contact angle.
membrane
A membrane is a selective barrier; it allows some things to pass through but stops others. Such things may be molecules, ions, or other small particles. Membranes can be generally classified into synthetic membranes and biological membranes. ...
, created between two rigid bodies with an arbitrary shape. Capillary bridges also may form between two liquids. Plateau defined a sequence of capillary shapes known as (1) nodoid with 'neck', (2) catenoid
In geometry, a catenoid is a type of surface, arising by rotating a catenary curve about an axis (a surface of revolution). It is a minimal surface, meaning that it occupies the least area when bounded by a closed space. It was formally descri ...
, (3) unduloid with 'neck', (4) cylinder
A cylinder (from ) has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base.
A cylinder may also be defined as an infin ...
, (5) unduloid with 'haunch' (6) sphere
A sphere () is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. A sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is th ...
and (7) nodoid with 'haunch'. The presence of capillary bridge, depending on their shapes, can lead to attraction or repulsion between the solid bodies.
The simplest cases of them are the axisymmetric ones. We distinguished three important classes of bridging, depending on connected bodies surface shapes:
* two planar surfaces (fig.1)
* planar surface and spherical particle (fig. 2)
* two spherical particles (in general, particles may not be of equal sizes, fig. 3)
 Capillary bridges and their properties may also be influenced by Earth gravity and by properties of the bridged surfaces. The bridging substance may be a liquid or a gas. The enclosing boundary is called the interface (
Capillary bridges and their properties may also be influenced by Earth gravity and by properties of the bridged surfaces. The bridging substance may be a liquid or a gas. The enclosing boundary is called the interface (capillary surface
In fluid mechanics and mathematics, a capillary surface is a surface that represents the interface between two different fluids. As a consequence of being a surface, a capillary surface has no thickness in slight contrast with most real fluid inte ...
). The interface is characterized by a particular surface tension.
History
Capillary bridges have been studied for over 200 years. The question was raised for the first time by Josef Louis Lagrange in 1760, and interest was further spread by the French astronomer and mathematician C. Delaunay. Delaunay found an entirely new class of axially symmetrical surfaces of constant mean curvature. The formulation and the proof of his theorem had a long story. It began with Euler's proposition of new figure, called ''catenoid''. (Much later, Kenmotsu solved the complex nonlinear equations, describing this class of surfaces. However, his solution is of little practical importance because it has no geometrical interpretation.) J. Plateau showed the existence of such shapes with given boundaries. The problem was named after himPlateau's problem
In mathematics, Plateau's problem is to show the existence of a minimal surface with a given boundary, a problem raised by Joseph-Louis Lagrange in 1760. However, it is named after Joseph Plateau who experimented with soap films. The problem ...
.Many scientists contributed to the solution of the problem. One of them is Thomas Young. Pierre Simon Laplace contributed the notion of capillary tension. Laplace even formulated the widely known nowadays condition for mechanical equilibrium between two fluids, divided by a capillary surface ''P''γ=Δ''P'' i.e. capillary pressure between two phases is balanced by their adjacent pressure difference.
A general survey on capillary bridge behavior in gravity field is completed by Myshkis and Babskii.A.D. Myshkis and V.G. Babskii, Low-Gravity Fluid Mechanics: Mathematical Theory of Capillary Phenomena, Springer-Verlag 1987
In the last century a lot of efforts were put of study of surface forces that drive capillary effects of bridging. There was established that these forces result from intermolecular forces and become significant in thin fluid gaps (<10 nm) between two surfaces.
The instability of capillary bridges was discussed in first time by Rayleigh.Strut, J. W., Lord Rayleigh, On the instability of jets, Proceedings of London Mathematical Society, v.10, pp. 4-13 (1878) He demonstrated that a liquid jet or capillary cylindrical surface became unstable when the ratio between its length, ''H'' to the radius ''R'', becomes bigger than 2π. In these conditions of small sinusoidal perturbations with wavelength bigger than its perimeter, the cylinder surface area becomes larger than the one of unperturbed cylinder with the same volume and thus it becomes unstable. Later, Hove formulated the variational requirements for the stability of axisymmetric capillary surfaces (unbounded) in absence of gravity and with disturbances constrained to constant volume. He first solved Young-Laplace equation for equilibrium shapes and showed that the Legendre condition for the second variation is always satisfied. Therefore, the stability is determined by the absence of negative eigenvalue of the linearized Young-Laplace equation. This approach of determining stability from second variation is used now widely. Perturbation methods became very successful despite that nonlinear nature of capillary interaction can limit their application. Other methods now include direct simulation. To that moment most methods for stability determination required calculation of equilibrium as a basis for perturbations. There appeared a new idea that stability may be deduced from equilibrium states. The proposition was further proven by Pitts for axisymmetric constant volume. In the following years Vogel extended the theory. He examined the case of axisymmetric capillary bridges with constant volumes and the stability changes correspond to turning points. The recent development of bifurcation theory proved that ''exchange of stability'' between turning points and branch points is a general phenomenon.
Applications and occurrences
Recent studies indicated that ancient Egyptians used the properties of sand to create capillary bridges by using water on it.A. Fall, B. Weber, M. Pakpour, N. Lenoir, N. Shahidzadeh, J. Fiscina, C. Wagner, and D. Bonn, Sliding Friction on Wet and Dry Sand Phys. Rev. Lett. 112, 175502,Published 29 April 2014 In this way, they reduced surface friction and were capable to move statues and heavy pyramid stones. Some contemporary arts, likesand art Sand art may refer to:
*Sand art and play, e.g. Sculpturing "building sand castles"
*Sandpainting
*Sand drawing
*Sand mandalas, Buddhist sand paintings
*Sand animation
Sand animation is the manipulation of sand to create animation. In performa ...
, are also close related to capability of water to bridge particles. In atomic force microscopy, when one works in higher humidity environment, their studies might be affected by the appearance of nano sized capillary bridges. These bridges appear when the working tip approaches the studied sample. Capillary bridges also play important role in soldering
Soldering (; ) is a process in which two or more items are joined by melting and putting a filler metal (solder) into the joint, the filler metal having a lower melting point than the adjoining metal. Unlike welding, soldering does not involv ...
process.
Djehutihotep
Djehutihotep ("''Thoth is satisfied''") was an ancient Egyptian nomarch of the fifteenth '' nomos'' of Upper Egypt (''" the Hare"'') during the twelfth dynasty, c. 1900 BC.
Biography
Djehutihotep lived under the reigns of Amenemhat II, Senu ...
depicting the transport of a colossal statue
AFM_-_detail.jpg , AFM
Soldering-PCB-b.jpg , Soldering
White_lipped_tree_frog_cairns_jan_8_2006.jpg, White lipped tree frog
Capillary bridges also widely spread in living nature. Bugs, flies, grasshoppers and tree frogs are capable to adhere to vertical rough surfaces because of their ability to inject wetting liquid into the pad-substrate contact area. This way is created long range attractive interaction due to the formation of capillary bridges. Many medical problems involving respiratory diseases, and the health of the body joints depend on tiny capillary bridges. Liquid bridges are now commonly used in growth of cell cultures because of the need to mimic work of living tissues in scientific research.
General equations
General solution for the profile of capillary is known from consideration of unduloid or nodoid curvature.Princen N.M., "The Equilibrium Shape of Interfaces, Drops and Bubbles Rigid and Deformable Particles at Interfaces" in Surface and Colloid Science, ed. E. Matijievich, (1969), v.3, New YorkLet's assume the following cylindrical coordinate system: ''z'' shows axis of revolution; ''r'' represents radial coordinate and ''φ'' is the angle between the normal and the positive ''z'' axis. The nodoid has vertical tangents at ''r'' = ''r''1 and ''r'' = ''r''2 and horizontal tangent at ''r'' = ''r''3. When ''φ'' is the angle between the normal to the interface and positive ''z'' axis then ''φ'' is equal to 90°, 0°, -90° for nodoid.
The Young-Laplace equation may be written in a form convenient for integration for axial symmetry : where ''R''1, ''R''2 are the radii of curvature and ''γ'' is interfacial surface tension.
The integration of the equation is called ''the first integral'' and it yields: Since:
One finds: After the integration, the obtained equation is called ''the second integral'':
where: F and E are
elliptic integral
In integral calculus, an elliptic integral is one of a number of related functions defined as the value of certain integrals, which were first studied by Giulio Fagnano and Leonhard Euler (). Their name originates from their originally arising in ...
s of first and second kind, and ''φ'' is related to r according to.The unduloid has only vertical tangents at ''r''=''r''1 and ''r''=''r''2, where ''φ'' = + 90. In a completely analogous way:
''The second integral'' for unduloid is obtained: where the relation between parameters k and φ are defined the same way as above. In the limiting case ''r''1=0, both nodoid and unduloid consist of a series of spheres. When ''r''1=''r''2. The last and the very interesting limiting case is ''catenoid''. The Laplace equation is reduced to:
It integration can be represented in very convenient form, in cylindrical coordinate system, called ''catenary equation'':
Equation (9) is important because it shows in some simplification all issues, related to the capillary bridges, transparent. Drawing in dimensionless coordinates exhibit a maximum, that distinguishes two branches. One of them is energetically favorable and come up to existence in statics while the other (in dashed line) is not energetically favorable. Maximum is important because when stretching quasi-equilibrium way capillary bridge, if maximum is reached, it breakage takes place. Catenoids with energetically unfavorable dimensions may form during process of dynamical stretching/pressing. Zero capillary pressure ''C''=0 is natural for classical catenoid (capillary soap surface stretched between two coaxial rings). When typical capillary bridge comes to catenoidal state of ''C'' = 0, despite that it surface properties are the same as classical catenoid, it is more appropriate to be presented as scaled by cube root of its volume rather than the radius, ''R''. The solution of ''the second integral'' is different in cases of oblate capillary bridges (nodoid and unduloid): where: F and E are again elliptic integrals of first and second kind, and φ is related to r according to: .
It is important to note that all described curves are found by rolling a conic section without slip along ''z'' axis. The unduloid is described by the focus of rolling ellipse, which can degenerate into a line, a sphere or a parabola, leading to the corresponding limiting cases. Similarly, a nodoid is described by the focus of a rolling hyperbola.
Well systematized summary of capillary bridges shapes is given in table 11.1 of Kralchevsky and Nagayama's book.
Statics between two flat surfaces
The mechanical equilibrium comprises the pressure balance on liquid/gas interface and the external force on plates, Δ''P'', balancing the capillary attraction or repulsion, , i.e. . Upon neglecting gravity effects and other external fields, the pressure balance is Δ''P''=''P''i - ''P''e (The indexes "i" and "e" denote correspondingly internal and external pressures). In case of axial symmetry, the equation for capillary pressure takes the form: where ''γ'' is interfacial liquid/gas tension; ''r'' is radial coordinate and ''φ'' is the angle between the axis symmetry and normal to interface generatrix.The first integral is easily obtained regarding dimensionless capillary pressure at the contact with surface:
where , dimensionless radius at the contact is and ''θ'' is the contact angle. The relation shows that capillary pressure can be positive or negative. The shape of capillary bridges is governed by the equation:
where the equation is obtained after substitution is made in Eq. () and scalling is introduced.
Thin liquid bridge
In contrast to cases with increasing height of capillary bridges, that poses variety of profile shapes, the flattening (thinning) toward zero thickness has much more universal character. The universality appears when ''H''<<''R'' (fig. 1). Equation (11) may be written: The generatrix converges to equation:Upon integration, the equation yields: The dimensionless circular radii 1/2C coincides with capillary bridge radii of curvature. The positive sign '+' represents generatrix profile of concave bridge and negative '-', oblate. For the convex capillary bridges, the circular generatrix is retained until the boundary of definition domain is reached while stretching. Near the beginning of self-initiated breakage kinetics, the bridge profile evolves consequently to an ellipse, parabola and possibly to hyperbola.
Definition domain
The observations, presented in fig. 5 indicate that a domain of capillary bridges existence can be defined. Therefore, if stretching of a liquid bridge it might discontinue its existence not only because of raising instabilities but also because of reaching of some points that the shape can not exist anymore. The estimation of definition domain requires manipulation of integrated equations for capillary bridge height and its volume. Both they are integrable but the integrals are improper. The applied method includes splitting of the integrals on two parts: singular but integrable analytically and regular but integrable only numerical way.After the integration, for the capillary bridge height is obtained Similar way for contact radius ''R'', is obtained the integrated equation where and In fig. 6 are shown number of stable static states of liquid capillary bridge, represented by two characteristic parameters: (i) dimensionless height that is obtained by scaling of capillary bridge height by cubic root of its volume Eq. () and (ii) its radius, also scaled by cubic root of volume, Eq. (). The partially analytical solutions, obtained for these two parameters, are presented above. The solutions somehow differs from widely accepted Plateau's approach y elliptical functions, Eq. () because they offer convenient numerical approach for integration of regular integrals, while irregular part of the equation was integrated analytically. These solutions became further a basis for prediction of capillary bridges quasi-equilibrium stretching and breakage for contact angles below 45°. The practical implementation allows to be identified not only the end of definition domain but also the exact behavior during the capillary bridge stretching, because in coordinates stretching forms an inclined line, where the inclination angle is proportional to the contact angle.
Concave capillary bridge
The case of concave capillary bridge is presented by isogones for contact angles below in fig. 6, . The isogones show well defined maximum . This maximum is noted by dot for each isogone. It again, similarly to a simple catenoid, separates two branches. The left branch is energetically favorable while the right one is energetically unfavourable.Cylindrical capillary bridge
This case is analyzed well by Rayleigh. Note that the definition domain in his case shows no limitations and it goes to infinity, fig. 6, . However, the breakage of cylindrical capillary bridges is usually observed. It takes place as result from well studied instability known now as Rayleigh instability. The definition domain for 90° isogone in shown in fig 6 by dashed line.Convex capillary bridge
The case of convex capillary bridges is presented in fig. 6, left from the domain of cylindrical case.Stability between two flat surfaces
Equilibrium shapes and stability limits for capillary liquid bridges are subject to many theoretical and experimental studies. Studies are mostly concentrated on investigation of bridges between equals disks under gravitational conditions. It is well known that for each value of theBond number
Bond or bonds may refer to:
Common meanings
* Bond (finance), a type of debt security
* Bail bond, a commercial third-party guarantor of surety bonds in the United States
* Chemical bond, the attraction of atoms, ions or molecules to form chemical ...
, defined as (where: ''g'' is Earth gravitational acceleration, ''γ'' is the surface tension and ''R'' is radius of the contact) the stability diagram can be represented by a single closed piecewise curve on the slenderness/dimensionless volume plane. Slenderness is defined as , and the dimensionless volume is capillary bridge volume divided on cylinder volume with the same height, ''H'' and radius ''R'': .
If both slenderness and liquid volume are small enough, the stability limits are governed by detachment of liquid shape from the edges of the disks (three-phase contact line), AB line in fig. 7. The line BC represents minimum in volume that corresponds to axisymmetrical breakage. It is known in literature as ''minimum volume stability'' limit. The curve CA represents another limit to stability, characterizing maximum volume. It is upper bound to the stability region. There also exists a transition region between minimum and maximum volume stability. It is not yet clearly defined and thus is noted by dashed line in fig. 7.
See also
*Eötvös number In fluid dynamics the Eötvös number (Eo), also called the Bond number (Bo), is a dimensionless number
measuring the importance of gravitational forces compared to surface tension forces for the movement of liquid front. Alongside the Capillary n ...
* Capillary condensation
References
{{DEFAULTSORT:Capillary bridges Fluid statics