Cutting-plane method on:
[Wikipedia]
[Google]
[Amazon]
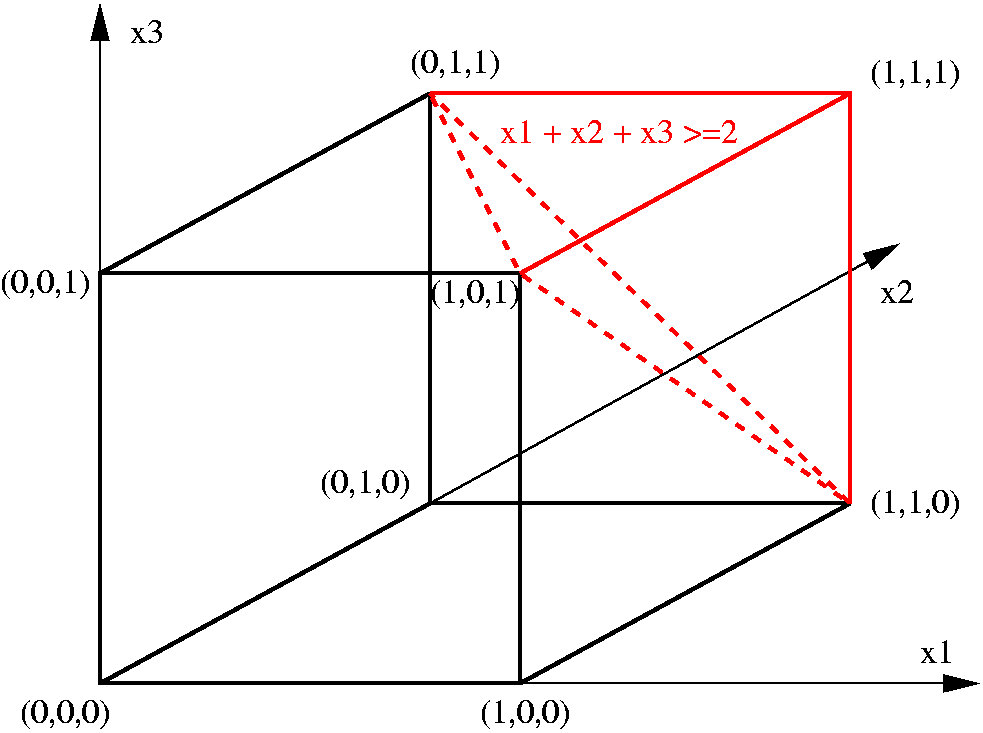 In
In
* Cornuéjols, Gérard (2007). Revival of the Gomory Cuts in the 1990s. ''Annals of Operations Research'', Vol. 149 (2007), pp. 63–66.
"Integer Programming" Section 9.8
''Applied Mathematical Programming'' Chapter 9 Integer Programming (full text). Bradley, Hax, and Magnanti (Addison-Wesley, 1977) {{Optimization algorithms, convex Optimization algorithms and methods
 In
In mathematical
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criteria, from some set of available alternatives. It is generally divided into two subfiel ...
, the cutting-plane method is any of a variety of optimization methods that iteratively refine a feasible set or objective function by means of linear inequalities, termed ''cuts''. Such procedures are commonly used to find integer
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative in ...
solutions to mixed integer linear programming (MILP) problems, as well as to solve general, not necessarily differentiable convex optimization
Convex optimization is a subfield of mathematical optimization that studies the problem of minimizing convex functions over convex sets (or, equivalently, maximizing concave functions over convex sets). Many classes of convex optimization problems ...
problems. The use of cutting planes to solve MILP was introduced by Ralph E. Gomory.
Cutting plane methods for MILP work by solving a non-integer linear program, the linear relaxation of the given integer program. The theory of Linear Programming dictates that under mild assumptions (if the linear program has an optimal solution, and if the feasible region does not contain a line), one can always find an extreme point or a corner point that is optimal. The obtained optimum
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criteria, from some set of available alternatives. It is generally divided into two subfiel ...
is tested for being an integer solution. If it is not, there is guaranteed to exist a linear inequality that ''separates'' the optimum from the convex hull
In geometry, the convex hull, convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space, ...
of the true feasible set. Finding such an inequality is the ''separation problem'', and such an inequality is a ''cut''. A cut can be added to the relaxed linear program. Then, the current non-integer solution is no longer feasible to the relaxation. This process is repeated until an optimal integer solution is found.
Cutting-plane methods for general convex continuous optimization and variants are known under various names: Kelley's method, Kelley–Cheney–Goldstein method, and bundle method
Subgradient methods are convex optimization methods which use Subderivative, subderivatives. Originally developed by Naum Z. Shor and others in the 1960s and 1970s, subgradient methods are convergent when applied even to a non-differentiable object ...
s. They are popularly used for non-differentiable convex minimization, where a convex objective function and its subgradient
In mathematics, the subderivative (or subgradient) generalizes the derivative to convex functions which are not necessarily differentiable. The set of subderivatives at a point is called the subdifferential at that point. Subderivatives arise in c ...
can be evaluated efficiently but usual gradient methods for differentiable optimization can not be used. This situation is most typical for the concave maximization of Lagrangian dual functions. Another common situation is the application of the Dantzig–Wolfe decomposition
Dantzig–Wolfe decomposition is an algorithm for solving linear programming problems with special structure. It was originally developed by George Dantzig and Philip Wolfe and initially published in 1960. Many texts on linear programming have s ...
to a structured optimization problem in which formulations with an exponential number of variables are obtained. Generating these variables on demand by means of delayed column generation
Column generation or delayed column generation is an efficient algorithm for solving large linear programs.
The overarching idea is that many linear programs are too large to consider all the variables explicitly. The idea is thus to start by so ...
is identical to performing a cutting plane on the respective dual problem.
History
Cutting planes were proposed by Ralph Gomory in the 1950s as a method for solving integer programming and mixed-integer programming problems. However, most experts, including Gomory himself, considered them to be impractical due to numerical instability, as well as ineffective because many rounds of cuts were needed to make progress towards the solution. Things turned around when in the mid-1990s Gérard Cornuéjols and co-workers showed them to be very effective in combination with branch-and-bound (called branch-and-cut) and ways to overcome numerical instabilities. Nowadays, all commercial MILP solvers use Gomory cuts in one way or another. Gomory cuts are very efficiently generated from a simplex tableau, whereas many other types of cuts are either expensive or even NP-hard to separate. Among other general cuts for MILP, most notably lift-and-project dominates Gomory cuts.Gomory's cut
Let an integer programming problem be formulated (incanonical form
In mathematics and computer science, a canonical, normal, or standard form of a mathematical object is a standard way of presenting that object as a mathematical expression. Often, it is one which provides the simplest representation of an obje ...
) as:
:
where A is a matrix and b , c is a vector. The vector x is unknown and is to be found in order to maximize the objective while respecting the linear constraints.
General idea
The method proceeds by first dropping the requirement that the xi be integers and solving the associated relaxed linear programming problem to obtain a basic feasible solution. Geometrically, this solution will be a vertex of the convex polytope consisting of all feasible points. If this vertex is not an integer point then the method finds a hyperplane with the vertex on one side and all feasible integer points on the other. This is then added as an additional linear constraint to exclude the vertex found, creating a modified linear program. The new program is then solved and the process is repeated until an integer solution is found.Step 1: solving the relaxed linear program
Using the simplex method to solve a linear program produces a set of equations of the form : where ''xi'' is a basic variable and the ''xjs are the nonbasic variables (i.e. the basic solution which is an optimal solution to the relaxed linear program is and ). We write coefficients and with a bar to denote the last tableau produced by the simplex method. These coefficients are different from the coefficients in the matrix A and the vector b.Step 2: Find a linear constraint
Consider now a basic variable which is not an integer. Rewrite the above equation so that the integer parts are added on the left side and the fractional parts are on the right side: : For any integer point in the feasible region, the left side is an integer since all the terms , , , are integers. The right side of this equation is strictly less than 1: indeed, is strictly less than 1 while is negative. Therefore the common value must be less than or equal to 0. So the inequality : must hold for any integer point in the feasible region. Furthermore, non-basic variables are equal to 0s in any basic solution and if ''xi'' is not an integer for the basic solution ''x'', :Conclusion
So the inequality above excludes the basic feasible solution and thus is a cut with the desired properties. More precisely, is negative for any integer point in the feasible region, and strictly positive for the basic feasible (non integer) solution of the relaxed linear program. Introducing a new slack variable xk for this inequality, a new constraint is added to the linear program, namely :Convex optimization
Cutting plane methods are also applicable in nonlinear programming. The underlying principle is to approximate thefeasible region
In mathematical optimization and computer science, a feasible region, feasible set, or solution space is the set of all possible points (sets of values of the choice variables) of an optimization problem that satisfy the problem's constraints, ...
of a nonlinear (convex) program by a finite set of closed half spaces and to solve a sequence of approximating linear program
Linear programming (LP), also called linear optimization, is a method to achieve the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements and objective are represented by linear relationships. Linear ...
s.
See also
*Benders' decomposition
Benders decomposition (or Benders' decomposition) is a technique in mathematical programming that allows the solution of very large linear programming problems that have a special block structure. This block structure often occurs in application ...
*Branch and cut
Branch and cut is a method of combinatorial optimization for solving integer linear programs (ILPs), that is, linear programming (LP) problems where some or all the unknowns are restricted to integer values. Branch and cut involves running a branc ...
*Branch and bound
Branch and bound (BB, B&B, or BnB) is a method for solving optimization problems by breaking them down into smaller sub-problems and using a bounding function to eliminate sub-problems that cannot contain the optimal solution.
It is an algorithm ...
* Column generation
*Dantzig–Wolfe decomposition
Dantzig–Wolfe decomposition is an algorithm for solving linear programming problems with special structure. It was originally developed by George Dantzig and Philip Wolfe and initially published in 1960. Many texts on linear programming have s ...
References
* * Avriel, Mordecai (2003). ''Nonlinear Programming: Analysis and Methods.'' Dover Publications. * Cornuéjols, Gérard (2008). Valid Inequalities for Mixed Integer Linear Programs. ''Mathematical Programming Ser. B'', (2008) 112:3–44.* Cornuéjols, Gérard (2007). Revival of the Gomory Cuts in the 1990s. ''Annals of Operations Research'', Vol. 149 (2007), pp. 63–66.
External links
"Integer Programming" Section 9.8
''Applied Mathematical Programming'' Chapter 9 Integer Programming (full text). Bradley, Hax, and Magnanti (Addison-Wesley, 1977) {{Optimization algorithms, convex Optimization algorithms and methods