Cut-point Line And Circle

In topology, a cut-point is a point of a connected space such that its removal causes the resulting space to be disconnected. If removal of a point doesn't result in disconnected spaces, this point is called a non-cut point.

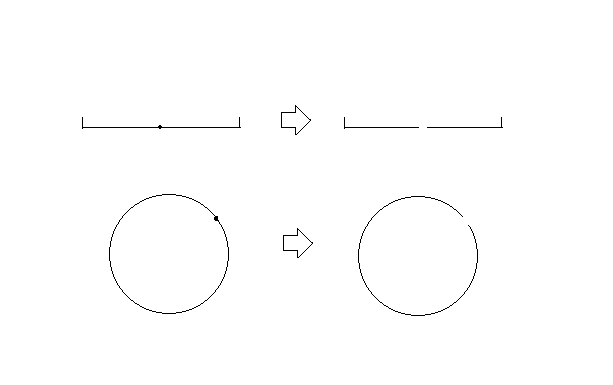
For example, every point of a line is a cut-point, while no point of a circle is a cut-point.

Cut-points are useful to determine whether two connected spaces are homeomorphic by counting the number of cut-points in each space. If two spaces have different number of cut-points, they are not homeomorphic. A classic example is using cut-points to show that lines and circles are not homeomorphic.

Cut-points are also useful in the characterization of topological continua, a class of spaces which combine the properties of compactness and connectedness and include many familiar spaces such as the unit interval, the circle, and the torus.

Definition

Formal definitions

A cut-point of a connected T₁ topological space ''X'', is a point ''p'' in ''X'' such that ''X'' - is not connected. A point which is not a cut-point is called a non-cut point.

A non-empty connected topological space X is a cut-point space if every point in X is a cut point of X.

Basic examples

*A closed interval ,bhas infinitely many cut-points. All points except for its end points are cut-points and the end-points are non-cut points.
*An open interval (a,b) also has infinitely many cut-points like closed intervals. Since open intervals don't have end-points, it has no non-cut points.
*A circle has no cut-points and it follows that every point of a circle is a non-cut point.

Notations

*A cutting of X is a set where p is a cut-point of X, U and V form a separation of X-.
*Also can be written as X\=U, V.

Theorems

Cut-points and homeomorphisms

* Cut-points are not necessarily preserved under continuous functions. For example: ''f'': , 2→ R², given by ''f''(''x'') = (cos ''x'', sin ''x''). Every point of the interval (except the two endpoints) is a cut-point, but f(x) forms a circle which has no cut-points.
* Cut-points are preserved under homeomorphisms. Therefore, cut-point is a topological invariant.

Cut-points and continua

* Every continuum (compact connected Hausdorff space) with more than one point, has at least two non-cut points. Specifically, each open set which forms a separation of resulting space contains at least one non-cut point.
* Every continuum with exactly two noncut-points is homeomorphic to the unit interval.
* If K is a continuum with points a,b and K- isn't connected, K is homeomorphic to the unit circle.

Topological properties of cut-point spaces

* Let X be a connected space and x be a cut point in X such that X\=A, B. Then is either open or closed. if is open, A and B are closed. If is closed, A and B are open.
* Let X be a cut-point space. The set of closed points of X is infinite.

Irreducible cut-point spaces

Definitions

A cut-point space is irreducible if no proper subset of it is a cut-point space.

The Khalimsky line: Let $\mathbb$ be the set of the integers and $B=\ \cup \$ where $B$ is a basis for a topology on $\mathbb$. The Khalimsky line is the set $\mathbb$ endowed with this topology. It's a cut-point space. Moreover, it's irreducible.

Theorem

* A topological space $X$ is an irreducible cut-point space if and only if X is homeomorphic to the Khalimsky line.

See also

Cut point (graph theory)

References

*
*
* {{cite book, title=General Topology, publisher=Dover Publications, year=2004, isbn=0-486-43479-6, author=Willard, Stephen (Originally published by Addison-Wesley Publishing Company, Inc. in 1970.)
General topology