Critical Point (network Science)

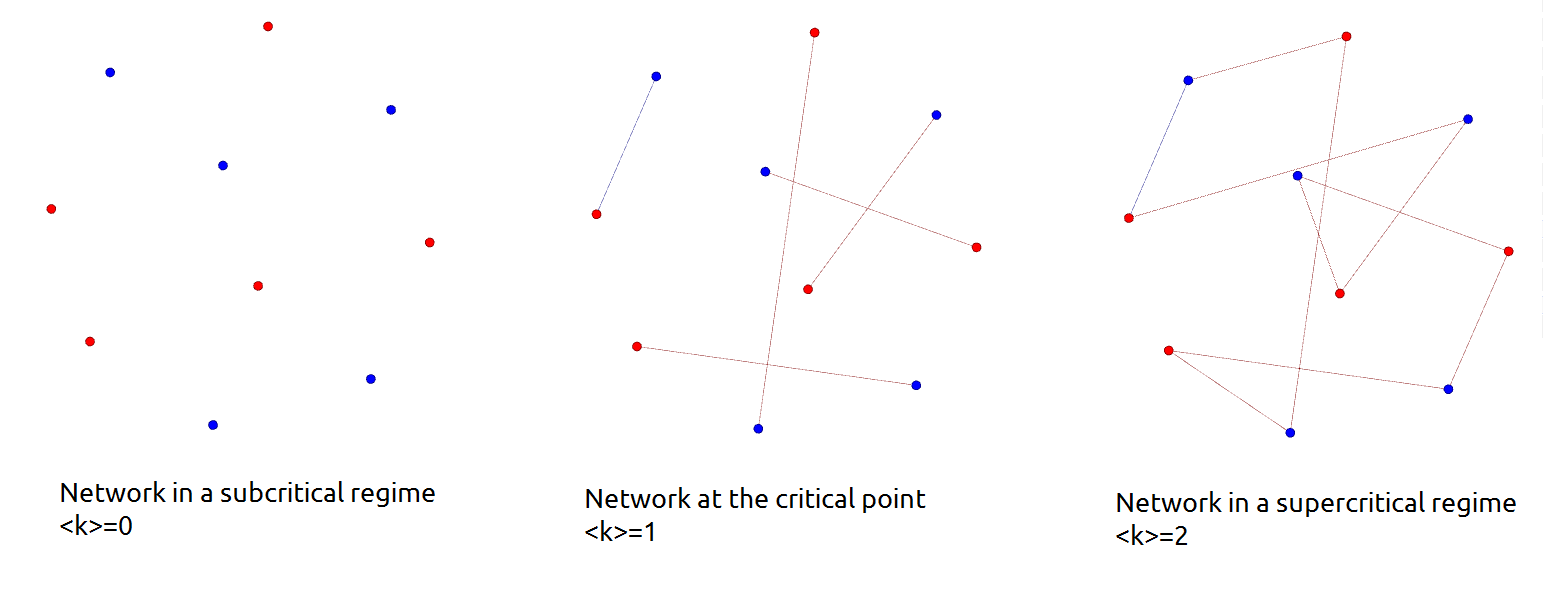
In network science, a critical point is a value of average degree, which separates random networks that have a giant component from those that do not (i.e. it separates a network in a subcritical regime from one in a supercritical regime). Considering a random network with an average degree $\langle k\rangle$ the critical point is

$\langle k\rangle = 1$

where the average degree is defined by the fraction of the number of edges ($e$) and nodes ($N$) in the network, that is $\langle k\rangle =\frac$.

Subcritical regime

In a subcritical regime the network has no giant component, only small clusters. In the special case of $\langle k\rangle =0$ the network is not connected at all. A random network is in a subcritical regime until the average degree exceeds the critical point, that is the network is in a subcritical regime as long as

$\langle k\rangle <1$.

Supercritical regime

In a supercritical regime, in contrary to the subcritical regime the network has a giant component. In the special case of $\langle k\rangle =N-1$ the network is complete (see complete graph). A random network is in a supercritical regime if the average degree exceeds the critical point, that is if

$\langle k\rangle >1$.

Example on different regimes

Consider a speed dating event as an example, with the participants as the nodes of the network. At the beginning of the event, people do not know anyone else. In this case the network is in a subcritical regime, that is, there is no giant component in the network (even if there are a couple of people, who know each other). After the first round of dates, everyone knows exactly one other person. There is still no giant component in the network, the average degree is $\langle k\rangle = 1$, that is, everyone knows one other person on average, meaning that the network is at the critical point. After the second round, the average degree of the network exceeds the critical point, and the giant component is present. In this specific case, the average degree is $\langle k\rangle = 2$. The network is in a supercritical regime.

See also

* Graph theory
* Percolation theory
* Complex network
* Random graph

References

{{reflist

Networks
Network theory