Cornu Spiral on:
[Wikipedia]
[Google]
[Amazon]
 An Euler spiral is a curve whose
An Euler spiral is a curve whose
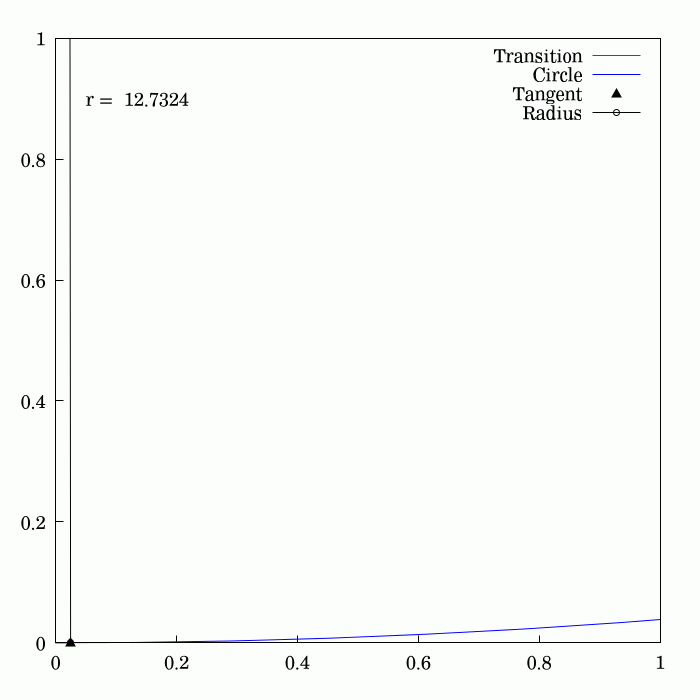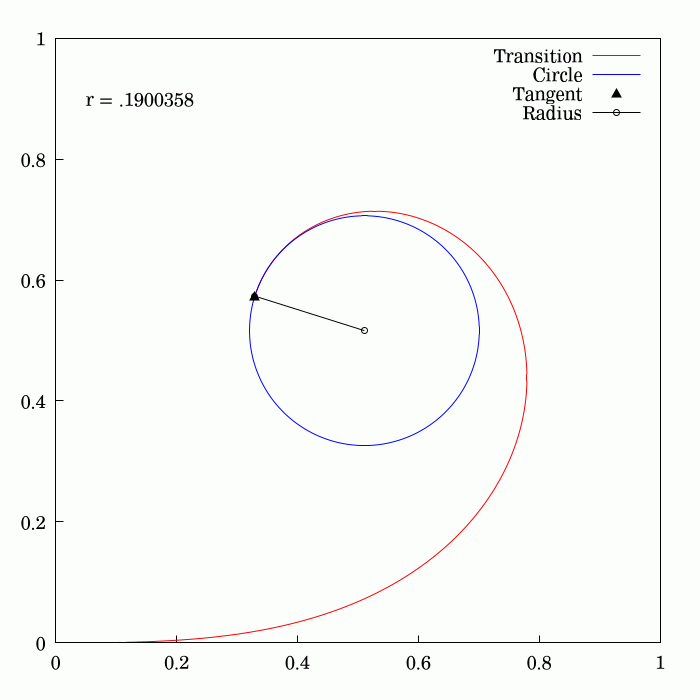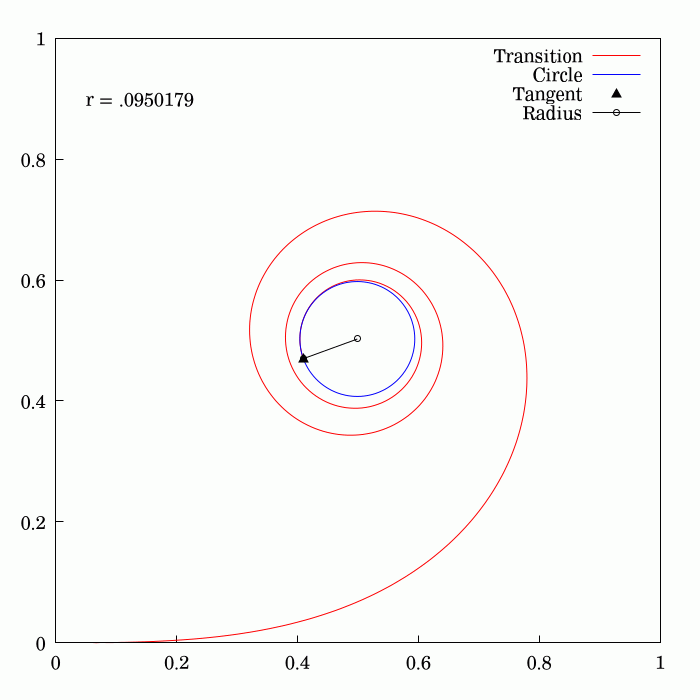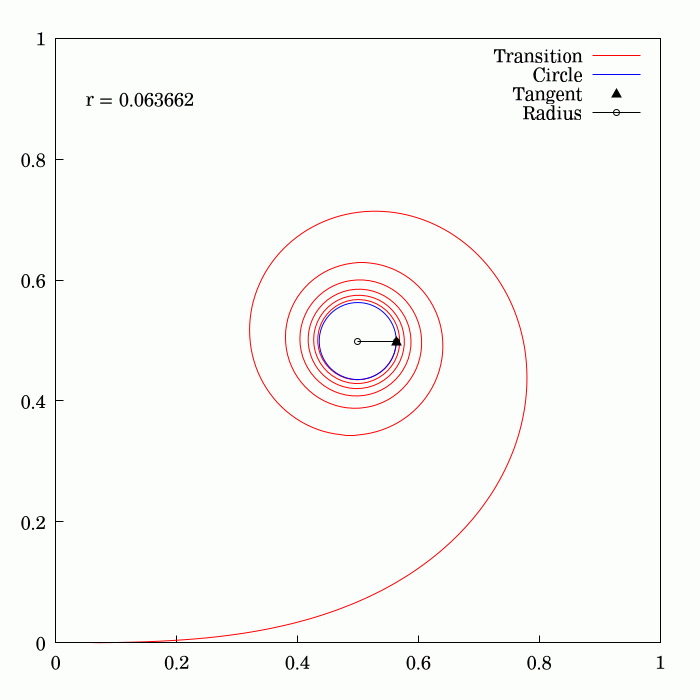 To travel along a circular path, an object needs to be subject to a centripetal acceleration (for example: the Moon circles around the Earth because of gravity; a car turns its front wheels inward to generate a centripetal force). If a vehicle traveling on a straight path were to suddenly transition to a tangential circular path, it would require centripetal acceleration suddenly switching at the tangent point from zero to the required value; this would be difficult to achieve (think of a driver instantly moving the steering wheel from straight line to turning position, and the car actually doing it), putting mechanical stress on the vehicle's parts, and causing much discomfort (due to lateral jerk).
On early railroads this instant application of lateral force was not an issue since low speeds and wide-radius curves were employed (lateral forces on the passengers and the lateral sway was small and tolerable). As speeds of rail vehicles increased over the years, it became obvious that an easement is necessary, so that the centripetal acceleration increases linearly with the traveled distance. Given the expression of centripetal acceleration , the obvious solution is to provide an easement curve whose curvature, , increases linearly with the traveled distance. This geometry is an Euler spiral.
Unaware of the solution of the geometry by Leonhard Euler,
To travel along a circular path, an object needs to be subject to a centripetal acceleration (for example: the Moon circles around the Earth because of gravity; a car turns its front wheels inward to generate a centripetal force). If a vehicle traveling on a straight path were to suddenly transition to a tangential circular path, it would require centripetal acceleration suddenly switching at the tangent point from zero to the required value; this would be difficult to achieve (think of a driver instantly moving the steering wheel from straight line to turning position, and the car actually doing it), putting mechanical stress on the vehicle's parts, and causing much discomfort (due to lateral jerk).
On early railroads this instant application of lateral force was not an issue since low speeds and wide-radius curves were employed (lateral forces on the passengers and the lateral sway was small and tolerable). As speeds of rail vehicles increased over the years, it became obvious that an easement is necessary, so that the centripetal acceleration increases linearly with the traveled distance. Given the expression of centripetal acceleration , the obvious solution is to provide an easement curve whose curvature, , increases linearly with the traveled distance. This geometry is an Euler spiral.
Unaware of the solution of the geometry by Leonhard Euler,
The Cornu spiral
''Hyperphysics'' (2002) ''(Uses πt²/2 instead of t².)'' * Milton Abramowitz and Irene A. Stegun, eds. '' Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables.'' New York: Dover, 1972.
(See Chapter 7)
' *
Interactive example with JSXGraphEuler's spiral-based map projection
{{DEFAULTSORT:Euler Spiral Transportation engineering Calculus Plane curves Spirals
curvature
In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane.
For curves, the canonic ...
changes linearly with its curve length (the curvature of a circular curve is equal to the reciprocal of the radius). Euler spirals are also commonly referred to as spiros, clothoids, or Cornu spirals.
Euler spirals have applications to diffraction
Diffraction is defined as the interference or bending of waves around the corners of an obstacle or through an aperture into the region of geometrical shadow of the obstacle/aperture. The diffracting object or aperture effectively becomes a s ...
computations. They are also widely used in railway and highway engineering to design transition curves between straight and curved sections of railway or roads. A similar application is also found in photonic integrated circuit
A photonic integrated circuit (PIC) or integrated optical circuit is a microchip containing two or more photonic components which form a functioning circuit. This technology detects, generates, transports, and processes light. Photonic integrated c ...
s. The principle of linear variation of the curvature of the transition curve between a tangent and a circular curve defines the geometry of the Euler spiral:
*Its curvature begins with zero at the straight section (the tangent) and increases linearly with its curve length.
*Where the Euler spiral meets the circular curve, its curvature becomes equal to that of the latter.
Applications
Track transition curve
 To travel along a circular path, an object needs to be subject to a centripetal acceleration (for example: the Moon circles around the Earth because of gravity; a car turns its front wheels inward to generate a centripetal force). If a vehicle traveling on a straight path were to suddenly transition to a tangential circular path, it would require centripetal acceleration suddenly switching at the tangent point from zero to the required value; this would be difficult to achieve (think of a driver instantly moving the steering wheel from straight line to turning position, and the car actually doing it), putting mechanical stress on the vehicle's parts, and causing much discomfort (due to lateral jerk).
On early railroads this instant application of lateral force was not an issue since low speeds and wide-radius curves were employed (lateral forces on the passengers and the lateral sway was small and tolerable). As speeds of rail vehicles increased over the years, it became obvious that an easement is necessary, so that the centripetal acceleration increases linearly with the traveled distance. Given the expression of centripetal acceleration , the obvious solution is to provide an easement curve whose curvature, , increases linearly with the traveled distance. This geometry is an Euler spiral.
Unaware of the solution of the geometry by Leonhard Euler,
To travel along a circular path, an object needs to be subject to a centripetal acceleration (for example: the Moon circles around the Earth because of gravity; a car turns its front wheels inward to generate a centripetal force). If a vehicle traveling on a straight path were to suddenly transition to a tangential circular path, it would require centripetal acceleration suddenly switching at the tangent point from zero to the required value; this would be difficult to achieve (think of a driver instantly moving the steering wheel from straight line to turning position, and the car actually doing it), putting mechanical stress on the vehicle's parts, and causing much discomfort (due to lateral jerk).
On early railroads this instant application of lateral force was not an issue since low speeds and wide-radius curves were employed (lateral forces on the passengers and the lateral sway was small and tolerable). As speeds of rail vehicles increased over the years, it became obvious that an easement is necessary, so that the centripetal acceleration increases linearly with the traveled distance. Given the expression of centripetal acceleration , the obvious solution is to provide an easement curve whose curvature, , increases linearly with the traveled distance. This geometry is an Euler spiral.
Unaware of the solution of the geometry by Leonhard Euler, Rankine Rankine is a surname. Notable people with the surname include:
* William Rankine (1820–1872), Scottish engineer and physicist
** Rankine body an elliptical shape of significance in fluid dynamics, named for Rankine
** Rankine scale, an absolute-te ...
cited the cubic curve (a polynomial curve of degree 3), which is an approximation of the Euler spiral for small angular changes in the same way that a parabola is an approximation to a circular curve.
Marie Alfred Cornu (and later some civil engineers) also solved the calculus of the Euler spiral independently. Euler spirals are now widely used in rail and highway engineering for providing a transition or an easement between a tangent and a horizontal circular curve.
Optics
The Cornu spiral can be used to describe adiffraction
Diffraction is defined as the interference or bending of waves around the corners of an obstacle or through an aperture into the region of geometrical shadow of the obstacle/aperture. The diffracting object or aperture effectively becomes a s ...
pattern.
Consider a plane wave with phasor amplitude which is diffracted by a "knife edge" of height above on the plane. Then the diffracted wave field can be expressed as
where is the Fresnel integral function, which forms the Cornu spiral on the complex plane.
So, to simplify the calculation of plane wave attenuation as it is diffracted from the knife-edge, one can use the diagram of a Cornu spiral by representing the quantities as the physical distances between the points represented by and for appropriate and . This facilitates a rough computation of the attenuation of the plane wave by the knife edge of height at a location beyond the knife edge.
Integrated optics
Bends with continuously varying radius of curvature following the Euler spiral are also used to reduce losses inphotonic integrated circuit
A photonic integrated circuit (PIC) or integrated optical circuit is a microchip containing two or more photonic components which form a functioning circuit. This technology detects, generates, transports, and processes light. Photonic integrated c ...
s, either in singlemode waveguides, to smoothen the abrupt change of curvature and suppress coupling to radiation modes, or in multimode waveguides, in order to suppress coupling to higher order modes and ensure effective singlemode operation.
A pioneering and very elegant application of the Euler spiral to waveguides had been made as early as 1957, with a hollow metal waveguide for microwaves. There the idea was to exploit the fact that a straight metal waveguide can be physically bent to naturally take a gradual bend shape resembling an Euler spiral.
Auto racing
Motorsport author Adam Brouillard has shown the Euler spiral's use in optimizing the racing line during the corner entry portion of a turn.Typography and digital vector drawing
Raph Levien has released Spiro as a toolkit for curve design, especially font design, in 2007 under a free licence. This toolkit has been implemented quite quickly afterwards in the font design tool Fontforge and the digital vector drawing Inkscape.Map projection
Cutting a sphere along a spiral with width and flattening out the resulting shape yields an Euler spiral when tends to the infinity. If the sphere is the globe, this produces a map projection whose distortion tends to zero as tends to the infinity.Whisker shapes
Natural shapes of rat's mystacial pad vibrissae ( whiskers) are well approximated by pieces of the Euler spiral. When all these pieces for a single rat are assembled together, they span an interval extending from one coiled domain of the Euler spiral to the other.Formulation
Symbols
Expansion of Fresnel integral
If , which is the case for normalized Euler curve, then the Cartesian coordinates are given by Fresnel integrals (or Euler integrals):Normalization and conclusion
For a given Euler curve with: or then where The process of obtaining solution of of an Euler spiral can thus be described as: * Map of the original Euler spiral by multiplying with factor to of the normalized Euler spiral; * Find from the Fresnel integrals; and * Map to by scaling up (denormalize) with factor . Note that . In the normalization process, Then Generally the normalization reduces to a small value (less than 1) and results in good converging characteristics of the Fresnel integral manageable with only a few terms (at a price of increasednumerical instability
In the mathematics, mathematical subfield of numerical analysis, numerical stability is a generally desirable property of numerical algorithms. The precise definition of stability depends on the context. One is numerical linear algebra and the oth ...
of the calculation, especially for bigger values.).
Illustration
Given: Then and We scale down the Euler spiral by , i.e. 100 to normalized Euler spiral that has: and The two angles are the same. This thus confirms that the original and normalized Euler spirals are geometrically similar. The locus of the normalized curve can be determined from Fresnel Integral, while the locus of the original Euler spiral can be obtained by scaling up or denormalizing.Other properties of normalized Euler spirals
Normalized Euler spirals can be expressed as: or expressed as power series: The normalized Euler spiral will converge to a single point in the limit as the parameter L approaches infinity, which can be expressed as: Normalized Euler spirals have the following properties: and Note that also means , in agreement with the last mathematical statement.See also
*Archimedean spiral
The Archimedean spiral (also known as the arithmetic spiral) is a spiral named after the 3rd-century BC Greek mathematician Archimedes. It is the locus corresponding to the locations over time of a point moving away from a fixed point with a con ...
* Fresnel integral
* Geometric design of roads
* List of spirals
* Track transition curve
References
Notes
Sources
Further reading
* * *R. NaveThe Cornu spiral
''Hyperphysics'' (2002) ''(Uses πt²/2 instead of t².)'' * Milton Abramowitz and Irene A. Stegun, eds. '' Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables.'' New York: Dover, 1972.
(See Chapter 7)
' *
External links
Interactive example with JSXGraph
{{DEFAULTSORT:Euler Spiral Transportation engineering Calculus Plane curves Spirals