Complex Random Variable

In probability theory and statistics, complex random variables are a generalization of real-valued random variables to complex numbers, i.e. the possible values a complex random variable may take are complex numbers. Complex random variables can always be considered as pairs of real random variables: their real and imaginary parts. Therefore, the distribution of one complex random variable may be interpreted as the joint distribution of two real random variables.

Some concepts of real random variables have a straightforward generalization to complex random variables—e.g., the definition of the mean of a complex random variable. Other concepts are unique to complex random variables.

Applications of complex random variables are found in digital signal processing, quadrature amplitude modulation and information theory.

Definition

A complex random variable $Z$ on the probability space $(\Omega,\mathcal,P)$ is a function $Z \colon \Omega \rightarrow \mathbb$ such that both its real part $\Re$ and its imaginary part $\Im$ are real random variables on $(\Omega,\mathcal,P)$.

Examples

Simple example

Consider a random variable that may take only the three complex values $1+i , 1-i , 2$ with probabilities as specified in the table. This is a simple example of a complex random variable.

The expectation of this random variable may be simply calculated:
\operatorname = \frac( 1+i ) + \frac( 1-i ) + \frac2 = \frac .

Uniform distribution

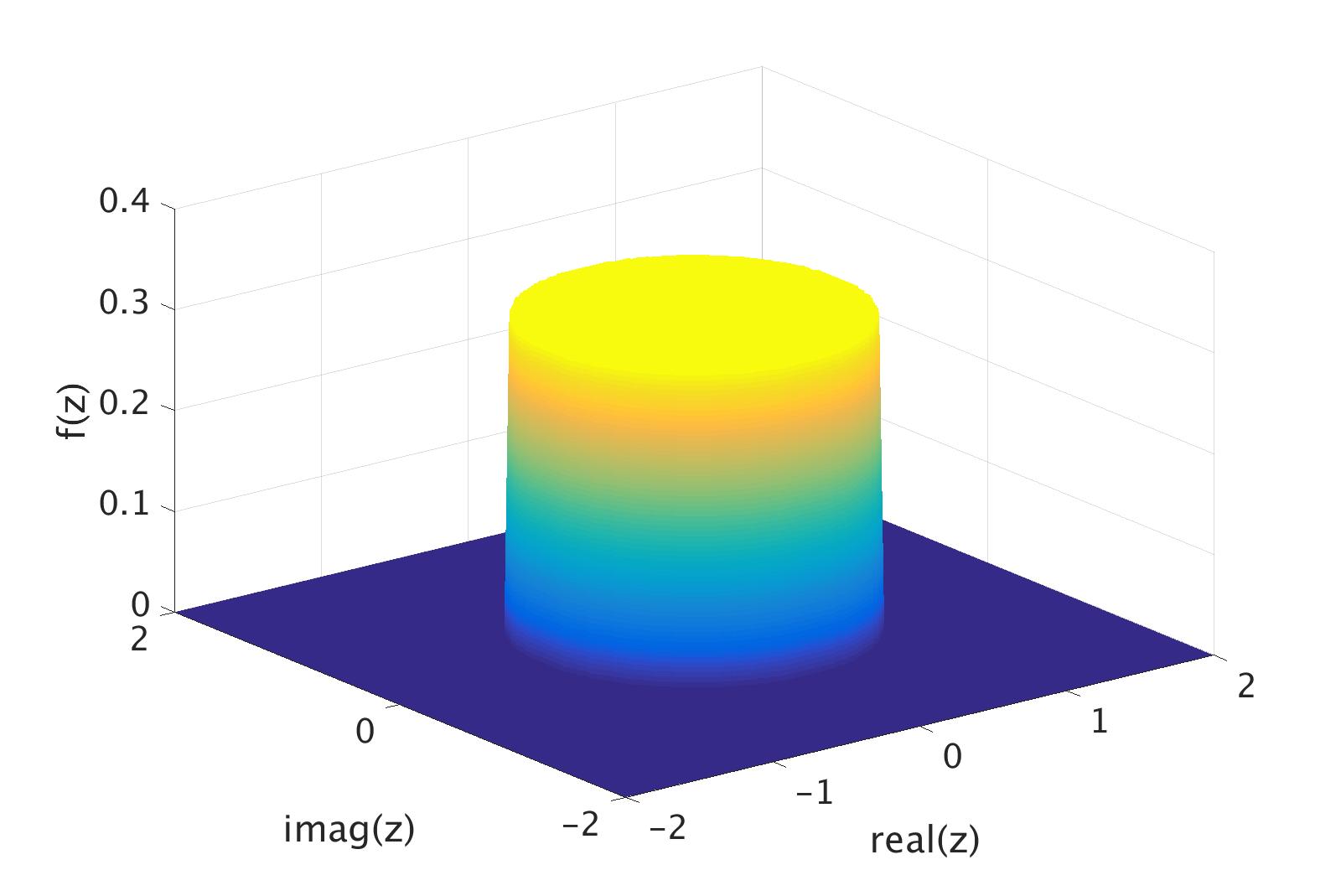
Another example of a complex random variable is the uniform distribution over the filled unit circle, i.e. the set $\$. This random variable is an example of a complex random variable for which the probability density function is defined. The density function is shown as the yellow disk and dark blue base in the following figure.

Complex normal distribution

Complex Gaussian random variables are often encountered in applications. They are a straightforward generalization of real Gaussian random variables. The following plot shows an example of the distribution of such a variable.

Cumulative distribution function

The generalization of the cumulative distribution function from real to complex random variables is not obvious because expressions of the form $P(Z \leq 1+3i)$ make no sense. However expressions of the form $P(\Re \leq 1, \Im \leq 3)$ make sense. Therefore, we define the cumulative distribution F_Z : \mathbb \to ,1/math> of a complex random variables via the joint distribution of their real and imaginary parts:

Probability density function

The probability density function of a complex random variable is defined as $f_Z(z)=f_(\Re,\Im)$, i.e. the value of the density function at a point $z \in \mathbb$ is defined to be equal to the value of the joint density of the real and imaginary parts of the random variable evaluated at the point $(\Re,\Im)$.

An equivalent definition is given by $f_Z(z)=\frac P(\Re \leq x , \Im \leq y)$ where $x=\Re$ and $y=\Im$.

As in the real case the density function may not exist.

Expectation

The expectation of a complex random variable is defined based on the definition of the expectation of a real random variable:

Note that the expectation of a complex random variable does not exist if \operatorname Re or \operatorname Im does not exist.

If the complex random variable $Z$ has a probability density function $f_Z(z)$, then the expectation is given by \operatorname \int\int_z \cdot f_Z(z) dx dy.

If the complex random variable $Z$ has a probability mass function $p_Z(z)$, then the expectation is given by \operatorname \sum_z \cdot p_Z(z).

;Properties
Whenever the expectation of a complex random variable exists, taking the expectation and complex conjugation commute:
: \overline=\operatorname overline Z.

The expected value operator \operatorname cdot/math> is linear in the sense that

:$\operatorname$Z + bW= a\operatorname + b\operatorname

for any complex coefficients $a,b$ even if $Z$ and $W$ are not independent.

Variance and pseudo-variance

The variance is defined in terms of absolute squares as:

;Properties
The variance is always a nonnegative real number. It is equal to the sum of the variances of the real and imaginary part of the complex random variable:

: \operatorname \operatorname Re\operatorname Im.

The variance of a linear combination of complex random variables may be calculated using the following formula:

: \operatorname\left sum_^N a_Z_k \right= \sum_^N \sum_^N a_\overline\operatorname _i,Z_j

Pseudo-variance

The pseudo-variance is a special case of the pseudo-covariance and is defined in terms of ordinary complex squares, given by:

Unlike the variance of $Z$, which is always real and positive, the pseudo-variance of $Z$ is in general complex.

Covariance matrix of real and imaginary parts

For a general complex random variable, the pair $(\Re,\Im)$ has a covariance matrix of the form:

:
\begin
\operatorname Re& \operatorname Im,\Re\\
\operatorname Re,\Im& \operatorname Im
\end

The matrix is symmetric, so \operatorname Re,\Im= \operatorname Im,\Re/math>

Its elements equal:
: \begin
& \operatorname Re= \tfrac\operatorname(\operatorname_ + \operatorname_) \\
& \operatorname Im= \tfrac\operatorname(\operatorname_ - \operatorname_) \\
& \operatorname Re,\Im= \tfrac\operatorname(\operatorname_) \\
\end
Conversely:
: \begin
& \operatorname_ = \operatorname Re+ \operatorname Im\\
& \operatorname_ = \operatorname Re- \operatorname Im+ i2 \operatorname Re,\Im \end

Covariance and pseudo-covariance

The covariance between two complex random variables $Z,W$ is defined as

Notice the complex conjugation of the second factor in the definition.

In contrast to real random variables, we also define a pseudo-covariance (also called complementary variance):

The second order statistics are fully characterized by the covariance and the pseudo-covariance.

;Properties
The covariance has the following properties:
* \operatorname ,W\overline (Conjugate symmetry)
* \operatorname alpha Z,W\alpha\operatorname ,W/math> (Sesquilinearity)
* \operatorname ,\alpha W\overline\operatorname ,W/math>
* $\operatorname$_1+Z_2,W\operatorname _1,W\operatorname _2,W/math>
* \operatorname ,W_1+W_2\operatorname ,W_1\operatorname ,W_2/math>
* \operatorname ,Z
* Uncorrelatedness: two complex random variables $Z$ and $W$ are called uncorrelated if $\operatorname_=\operatorname_=0$ (see also: uncorrelatedness (probability theory)).
* Orthogonality: two complex random variables $Z$ and $W$ are called orthogonal if \operatorname \overline= 0.

Circular symmetry

Circular symmetry of complex random variables is a common assumption used in the field of wireless communication. A typical example of a circular symmetric complex random variable is the complex Gaussian random variable with zero mean and zero pseudo-covariance matrix.

A complex random variable $Z$ is circularly symmetric if, for any deterministic \phi \in \pi,\pi, the distribution of $e^Z$ equals the distribution of $Z$.

;Properties
By definition, a circularly symmetric complex random variable has
\operatorname = \operatorname^ Z= e^\operatorname for any $\phi$.

Thus the expectation of a circularly symmetric complex random variable can only be either zero or undefined.

Additionally,
\operatorname Z= \operatorname^ Z e^Z= e^ \operatorname Z for any $\phi$.

Thus the pseudo-variance of a circularly symmetric complex random variable can only be zero.

If $Z$ and $e^Z$ have the same distribution, the phase of $Z$ must be uniformly distributed over \pi,\pi/math> and independent of the amplitude of $Z$.

Proper complex random variables

The concept of proper random variables is unique to complex random variables, and has no correspondent concept with real random variables.

A complex random variable $Z$ is called proper if the following three conditions are all satisfied:
* \operatorname = 0
* \operatorname < \infty
* \operatorname ^2= 0
This definition is equivalent to the following conditions. This means that a complex random variable is proper if, and only if:
* \operatorname = 0
* \operatorname Re^2\operatorname Im^2neq\infty
* \operatorname Re\Im0

For a proper complex random variable, the covariance matrix of the pair $(\Re,\Im)$ has the following simple form:

:
\begin
\frac \operatorname & 0 \\
0 & \frac \operatorname
\end
.
I.e.:
: \begin
& \operatorname Re= \operatorname Im= \tfrac\operatorname \\
& \operatorname Re,\Im= 0 \\
\end

Cauchy-Schwarz inequality

The Cauchy-Schwarz inequality for complex random variables, which can be derived using the Triangle inequality and Hölder's inequality, is
:\left, \operatorname \left Z\overline \right\^2 \leq \left, \operatorname \left Z\overline \ \right\^2 \leq \operatorname \left Z, ^2 \right\operatorname\left W, ^2 \right/math>.

Characteristic function

The characteristic function of a complex random variable is a function $\mathbb \to \mathbb$ defined by

: \varphi_Z(\omega) = \operatorname \left e^ \right = \operatorname \left e^ \right

See also

*Central moment
*Complex random vector

References

{{reflist

Probability theory
Randomness
Algebra of random variables