Carlyle circle on:
[Wikipedia]
[Google]
[Amazon]
In
 Given the quadratic equation
:''x''2 − ''sx'' + ''p'' = 0
the circle in the
Given the quadratic equation
:''x''2 − ''sx'' + ''p'' = 0
the circle in the
''Geometrical and Graphical Solutions of Quadratic Equations''
The College Mathematics Journal, Vol. 21, No. 5 (Nov., 1990), pp. 362–369
JSTOR
JSTOR


 According to
According to
online copy (Google)
. Note that the comment about Carlyle is not contained in earlier editions of the book (1809, 1811). In 1867 the Austrian engineer
JSTOR
Eves used the circle in the modern sense in one of the exercises of his book ''Introduction to the History of Mathematics'' (1953) and pointed out the connection to Leslie and Carlyle. Later publications started to adopt the names ''Carlyle circle'', ''Carlyle method'' or ''Carlyle algorithm'', though in German speaking countries the term ''Lill circle'' (''Lill-Kreis'') is used as well.Rainer Kaenders (ed.), Reinhard Schmidt (ed.): ''Mit GeoGebra mehr Mathematik verstehen''. Springer Spektrum, 2nd edition, 2014, , pp
68-71
(German) DeTemple used in 1989 and 1991 Carlyle circles to devise compass-and-straightedge constructions for regular polygons, in particular the
JSTOR
mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
, a Carlyle circle (named for Thomas Carlyle
Thomas Carlyle (4 December 17955 February 1881) was a Scottish essayist, historian and philosopher. A leading writer of the Victorian era, he exerted a profound influence on 19th-century art, literature and philosophy.
Born in Ecclefechan, Dum ...
) is a certain circle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is const ...
in a coordinate plane
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine the position of the points or other geometric elements on a manifold such as Euclidean space. The order of the coordinates is si ...
associated with a quadratic equation
In algebra, a quadratic equation () is any equation that can be rearranged in standard form as
ax^2 + bx + c = 0\,,
where represents an unknown (mathematics), unknown value, and , , and represent known numbers, where . (If and then the equati ...
. The circle has the property that the solutions
Solution may refer to:
* Solution (chemistry), a mixture where one substance is dissolved in another
* Solution (equation), in mathematics
** Numerical solution, in numerical analysis, approximate solutions within specified error bounds
* Soluti ...
of the quadratic equation are the horizontal coordinates of the intersections of the circle with the horizontal axis
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in ...
. Carlyle circles have been used to develop ruler-and-compass construction
In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an ideali ...
s of regular polygon
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either convex p ...
s.
Definition
coordinate plane
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine the position of the points or other geometric elements on a manifold such as Euclidean space. The order of the coordinates is si ...
having the line segment
In geometry, a line segment is a part of a straight line that is bounded by two distinct end points, and contains every point on the line that is between its endpoints. The length of a line segment is given by the Euclidean distance between ...
joining the points ''A''(0, 1) and ''B''(''s'', ''p'') as a diameter is called the Carlyle circle of the quadratic equation.E. John Hornsby, Jr.''Geometrical and Graphical Solutions of Quadratic Equations''
The College Mathematics Journal, Vol. 21, No. 5 (Nov., 1990), pp. 362–369
JSTOR
JSTOR
Defining property
The defining property of the Carlyle circle can be established thus: the equation of the circle having the line segment ''AB'' as diameter is :''x''(''x'' − ''s'') + (''y'' − 1)(''y'' − ''p'') = 0. Theabscissa
In common usage, the abscissa refers to the (''x'') coordinate and the ordinate refers to the (''y'') coordinate of a standard two-dimensional graph.
The distance of a point from the y-axis, scaled with the x-axis, is called abscissa or x coo ...
s of the points where the circle intersects the ''x''-axis are the roots
A root is the part of a plant, generally underground, that anchors the plant body, and absorbs and stores water and nutrients.
Root or roots may also refer to:
Art, entertainment, and media
* ''The Root'' (magazine), an online magazine focusing ...
of the equation (obtained by setting ''y'' = 0 in the equation of the circle)
:''x''2 − ''sx'' + ''p'' = 0.
Construction of regular polygons



Regular pentagon
The problem of constructing a regularpentagon
In geometry, a pentagon (from the Greek πέντε ''pente'' meaning ''five'' and γωνία ''gonia'' meaning ''angle'') is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°.
A pentagon may be simpl ...
is equivalent to the problem of constructing the roots of the equation
:''z''5 − 1 = 0.
One root of this equation is ''z''0 = 1 which corresponds to the point ''P''0(1, 0). Removing the factor corresponding to this root, the other roots turn out to be roots of the equation
:''z''4 + ''z''3 + ''z''2 + ''z'' + 1 = 0.
These roots can be represented in the form ω, ω2, ω3, ω4 where ω = exp (2''i''/5). Let these correspond to the points ''P''1, ''P''2, ''P''3, ''P''4. Letting
:''p''1 = ω + ω4, ''p''2 = ω2 + ω3
we have
:''p''1 + ''p''2 = −1, ''p''1''p''2 = −1. (These can be quickly shown to be true by direct substitution into the quartic above and noting that ω6 = ω, and ω7 = ω2.)
So ''p''1 and ''p''2 are the roots of the quadratic equation
:''x''2 + ''x'' − 1 = 0.
The Carlyle circle associated with this quadratic has a diameter with endpoints at (0, 1) and (−1, −1) and center at (−1/2, 0). Carlyle circles are used to construct ''p''1 and ''p''2. From the definitions of ''p''1 and ''p''2 it also follows that
:''p''1 = 2 cos(2/5), ''p''2 = 2 cos(4/5).
These are then used to construct the points ''P''1, ''P''2, ''P''3, ''P''4.
This detailed procedure involving Carlyle circles for the construction of regular pentagon
In geometry, a pentagon (from the Greek πέντε ''pente'' meaning ''five'' and γωνία ''gonia'' meaning ''angle'') is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°.
A pentagon may be simpl ...
s is given below.
#Draw a circle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is const ...
in which to inscribe the pentagon and mark the center point ''O''.
#Draw a horizontal line through the center of the circle. Mark one intersection with the circle as point ''B''.
#Construct a vertical line through the center. Mark one intersection with the circle as point ''A''.
#Construct the point ''M'' as the midpoint
In geometry, the midpoint is the middle point of a line segment. It is equidistant from both endpoints, and it is the centroid both of the segment and of the endpoints. It bisects the segment.
Formula
The midpoint of a segment in ''n''-dimens ...
of ''O'' and ''B''.
#Draw a circle centered at ''M'' through the point ''A''. This is the Carlyle circle for ''x''2 + ''x'' − 1 = 0. Mark its intersection with the horizontal line (inside the original circle) as the point ''W'' and its intersection outside the circle as the point ''V''. These are the points ''p''1 and ''p''2 mentioned above.
#Draw a circle of radius ''OA'' and center ''W''. It intersects the original circle at two of the vertices of the pentagon.
#Draw a circle of radius ''OA'' and center ''V''. It intersects the original circle at two of the vertices of the pentagon.
#The fifth vertex is the intersection of the horizontal axis with the original circle.
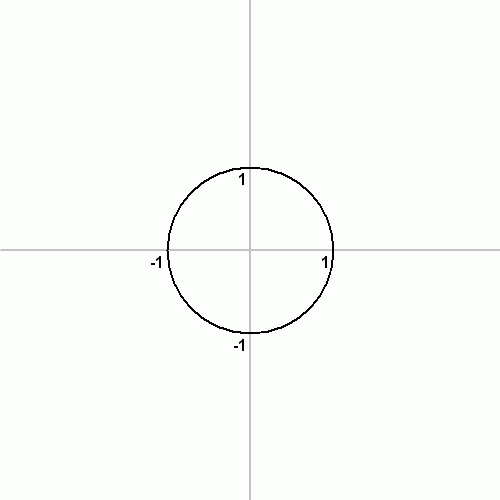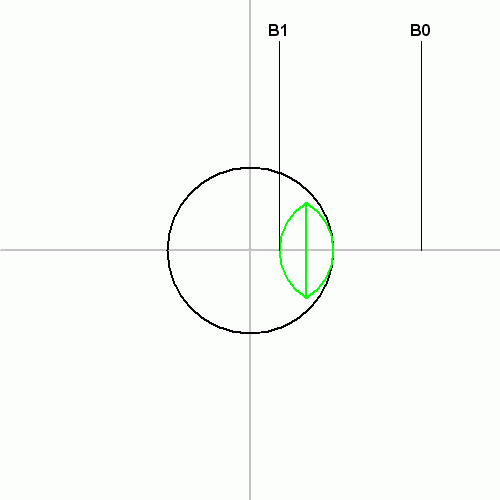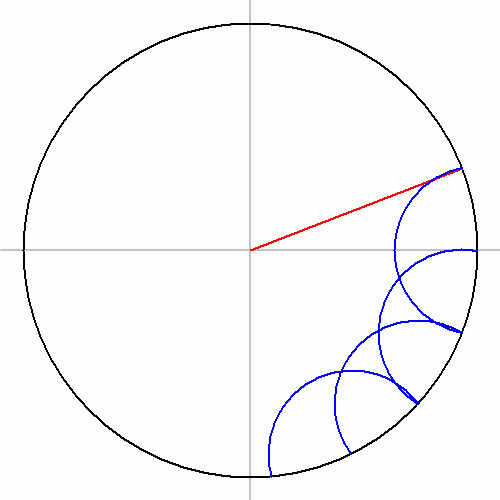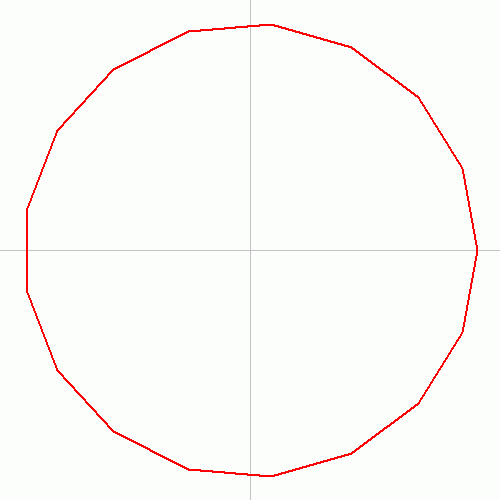
Regular heptadecagon
There is a similar method involving Carlyle circles to construct regularheptadecagon
In geometry, a heptadecagon, septadecagon or 17-gon is a seventeen-sided polygon.
Regular heptadecagon
A '' regular heptadecagon'' is represented by the Schläfli symbol .
Construction
As 17 is a Fermat prime, the regular heptadecagon is a ...
s. The figure to the right illustrates the procedure.
Regular 257-gon
To construct a regular257-gon
In geometry, a 257-gon is a polygon with 257 sides. The sum of the interior angles of any non- self-intersecting 257-gon is 45,900°.
Regular 257-gon
The area of a regular 257-gon is (with )
:A = \frac t^2 \cot \frac\approx 5255.751t^2.
A who ...
using Carlyle circles, as many as 24 Carlyle circles are to be constructed. One of these is the circle to solve the quadratic equation ''x''2 + ''x'' − 64 = 0.
Regular 65537-gon
There is a procedure involving Carlyle circles for the construction of a regular65537-gon
In geometry, a 65537-gon is a polygon with 65,537 (216 + 1) sides. The sum of the interior angles of any non–list of self-intersecting polygons, self-intersecting is 11796300°.
Regular 65537-gon
The area of a ''regular '' is (with )
:A = \f ...
. However there are practical problems for the implementation of the procedure; for example, it requires the construction of the Carlyle circle for the solution of the quadratic equation ''x''2 + ''x'' − 214 = 0.
History
Howard Eves
Howard Whitley Eves (10 January 1911, New Jersey – 6 June 2004) was an American mathematician, known for his work in geometry and the history of mathematics.
Eves received his B.S. from the University of Virginia, an M.A. from Harvard Universi ...
(1911–2004), the mathematician John Leslie (1766–1832) described the geometric construction of roots of a quadratic equation with a circle in his book ''Elements of Geometry'' and noted that this idea was provided by his former student Thomas Carlyle
Thomas Carlyle (4 December 17955 February 1881) was a Scottish essayist, historian and philosopher. A leading writer of the Victorian era, he exerted a profound influence on 19th-century art, literature and philosophy.
Born in Ecclefechan, Dum ...
(1795–1881). See for instance Hornsby, DeTemple or Howard Eves: ''An Introduction into the History of Mathematics''. Holt, Rinehart and Winston, 3rd edition, 1969, p. 73 However while the description in Leslie's book contains an analogous circle construction, it was presented solely in elementary geometric terms without the notion of a Cartesian coordinate system or a quadratic function and its roots:John Leslie: ''Elements of geometry and plane trigonometry: With an appendix, and copious notes and illustrations''. Archibald Constable & Co, 3. Ausgabe, 1817, pp. 176, 340online copy (Google)
. Note that the comment about Carlyle is not contained in earlier editions of the book (1809, 1811). In 1867 the Austrian engineer
Eduard Lill
Eduard Lill (1830–1900) was an Austrian engineer and army officer.
Life
Lill was born 20 October 1830 in Brüx ( Bohemia). From 1848 to 1849 he studied mathematics at the Czech Technical University in Prague and in 1850 he joined the military e ...
published a graphical method to determine the roots of a polynomial (Lill's method
In mathematics, Lill's method is a visual method of finding the real roots of a univariate polynomial of any degree. It was developed by Austrian engineer Eduard Lill in 1867. A later paper by Lill dealt with the problem of complex roots.
Lill ...
). If it is applied on a quadratic function, then it yields the trapezoid figure from Carlyle's solution to Leslie's problem (see graphic) with one of its sides being the diameter of the Carlyle circle. In an article from 1925 G. A. Miller pointed out that a slight modification of Lill's method applied to a normed quadratic function yields a circle that allows the geometric construction of the roots of that function and gave the explicit modern definition of what was later to be called Carlyle circle.G. A. Miller: ''Geometric Solution of the Quadratic Equation''. The Mathematical Gazette, Vol. 12, No. 179 (Dec., 1925), pp. 500–501JSTOR
Eves used the circle in the modern sense in one of the exercises of his book ''Introduction to the History of Mathematics'' (1953) and pointed out the connection to Leslie and Carlyle. Later publications started to adopt the names ''Carlyle circle'', ''Carlyle method'' or ''Carlyle algorithm'', though in German speaking countries the term ''Lill circle'' (''Lill-Kreis'') is used as well.Rainer Kaenders (ed.), Reinhard Schmidt (ed.): ''Mit GeoGebra mehr Mathematik verstehen''. Springer Spektrum, 2nd edition, 2014, , pp
68-71
(German) DeTemple used in 1989 and 1991 Carlyle circles to devise compass-and-straightedge constructions for regular polygons, in particular the
pentagon
In geometry, a pentagon (from the Greek πέντε ''pente'' meaning ''five'' and γωνία ''gonia'' meaning ''angle'') is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°.
A pentagon may be simpl ...
, the heptadecagon
In geometry, a heptadecagon, septadecagon or 17-gon is a seventeen-sided polygon.
Regular heptadecagon
A '' regular heptadecagon'' is represented by the Schläfli symbol .
Construction
As 17 is a Fermat prime, the regular heptadecagon is a ...
, the 257-gon
In geometry, a 257-gon is a polygon with 257 sides. The sum of the interior angles of any non- self-intersecting 257-gon is 45,900°.
Regular 257-gon
The area of a regular 257-gon is (with )
:A = \frac t^2 \cot \frac\approx 5255.751t^2.
A who ...
and the 65537-gon
In geometry, a 65537-gon is a polygon with 65,537 (216 + 1) sides. The sum of the interior angles of any non–list of self-intersecting polygons, self-intersecting is 11796300°.
Regular 65537-gon
The area of a ''regular '' is (with )
:A = \f ...
. Ladislav Beran described in 1999 how the Carlyle circle can be used to construct the complex roots of a normed quadratic function.Ladislav Beran: ''The Complex Roots of a Quadratic from a Circle''. The Mathematical Gazette, Vol. 83, No. 497 (Jul., 1999), pp. 287–291JSTOR
References
{{Thomas Carlyle, state=collapsed Euclidean geometry Polygons Constructible polygons Euclidean plane geometry Elementary algebra Equations Thomas Carlyle