The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling

tessellation A tessellation or tiling is the covering of a surface, often a plane (mathematics), plane, using one or more geometric shapes, called ''tiles'', with no overlaps and no gaps. In mathematics, tessellation can be generalized to high-dimensional ...

(or

honeycomb A honeycomb is a mass of Triangular prismatic honeycomb#Hexagonal prismatic honeycomb, hexagonal prismatic Beeswax, wax cells built by honey bees in their beehive, nests to contain their larvae and stores of honey and pollen. beekeeping, Beekee ...

) in

Euclidean 3-space Three-dimensional space (also: 3D space, 3-space or, rarely, tri-dimensional space) is a geometric setting in which three values (called ''parameters'') are required to determine the position of an element (i.e., point). This is the informal ...

. It is composed of alternating regular

octahedra In geometry, an octahedron (plural: octahedra, octahedrons) is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at ea ...

and

tetrahedra In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the o ...

in a ratio of 1:2. Other names include half cubic honeycomb, half cubic cellulation, or tetragonal disphenoidal cellulation.

John Horton Conway John Horton Conway (26 December 1937 – 11 April 2020) was an English mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory. He also made contributions to many branches ...

calls this honeycomb a tetroctahedrille, and its dual a dodecahedrille. R. Buckminster Fuller combines the two words octahedron and tetrahedron into octet truss, a rhombohedron consisting of one octahedron (or two square pyramids) and two opposite tetrahedra. It is

vertex-transitive In geometry, a polytope (e.g. a polygon or polyhedron) or a tiling is isogonal or vertex-transitive if all its vertices are equivalent under the symmetries of the figure. This implies that each vertex is surrounded by the same kinds of face in ...

with 8

and 6

around each

vertex Vertex, vertices or vertexes may refer to: Science and technology Mathematics and computer science *Vertex (geometry), a point where two or more curves, lines, or edges meet *Vertex (computer graphics), a data structure that describes the position ...

. It is

edge-transitive In geometry, a polytope (for example, a polygon or a polyhedron) or a tiling is isotoxal () or edge-transitive if its symmetries act transitively on its edges. Informally, this means that there is only one type of edge to the object: given two ...

with 2 tetrahedra and 2 octahedra alternating on each edge. It is part of an infinite family of

uniform honeycomb In geometry, a uniform honeycomb or uniform tessellation or infinite uniform polytope, is a vertex-transitive honeycomb made from uniform polytope facets. All of its vertices are identical and there is the same combination and arrangement of face ...

s called alternated hypercubic honeycombs, formed as an alternation of a hypercubic honeycomb and being composed of

demihypercube In geometry, demihypercubes (also called ''n-demicubes'', ''n-hemicubes'', and ''half measure polytopes'') are a class of ''n''- polytopes constructed from alternation of an ''n''- hypercube, labeled as ''hγn'' for being ''half'' of the hy ...

and

cross-polytope In geometry, a cross-polytope, hyperoctahedron, orthoplex, or cocube is a regular, convex polytope that exists in ''n''- dimensional Euclidean space. A 2-dimensional cross-polytope is a square, a 3-dimensional cross-polytope is a regular octahed ...

facets. It is also part of another infinite family of uniform honeycombs called

simplectic honeycomb In geometry, the simplectic honeycomb (or -simplex honeycomb) is a dimensional infinite series of honeycombs, based on the _n affine Coxeter group symmetry. It is represented by a Coxeter-Dynkin diagram as a cyclic graph of nodes with one nod ...

s. In this case of 3-space, the

cubic honeycomb The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation (or honeycomb) in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a re ...

is alternated, reducing the cubic cells to tetrahedra, and the deleted vertices create octahedral voids. As such it can be represented by an extended

Schläfli symbol In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations. The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to more ...

h as containing ''half'' the vertices of the cubic honeycomb. There is a similar honeycomb called

gyrated tetrahedral-octahedral honeycomb The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of alternating regular octahedra and tetrahedra in a ratio of 1:2. Other names incl ...

which has layers rotated 60 degrees so half the edges have neighboring rather than alternating tetrahedra and octahedra. The tetrahedral-octahedral honeycomb can have its symmetry doubled by placing tetrahedra on the octahedral cells, creating a nonuniform honeycomb consisting of

and

(as triangular antiprisms). Its vertex figure is an order-3 truncated triakis tetrahedron. This honeycomb is the dual of the

triakis truncated tetrahedral honeycomb The triakis truncated tetrahedral honeycomb is a space-filling tessellation (or honeycomb) in Euclidean 3-space made up of triakis truncated tetrahedra. It was discovered in 1914. Voronoi tessellation It is the Voronoi tessellation of the carbo ...

, with triakis truncated tetrahedral cells.

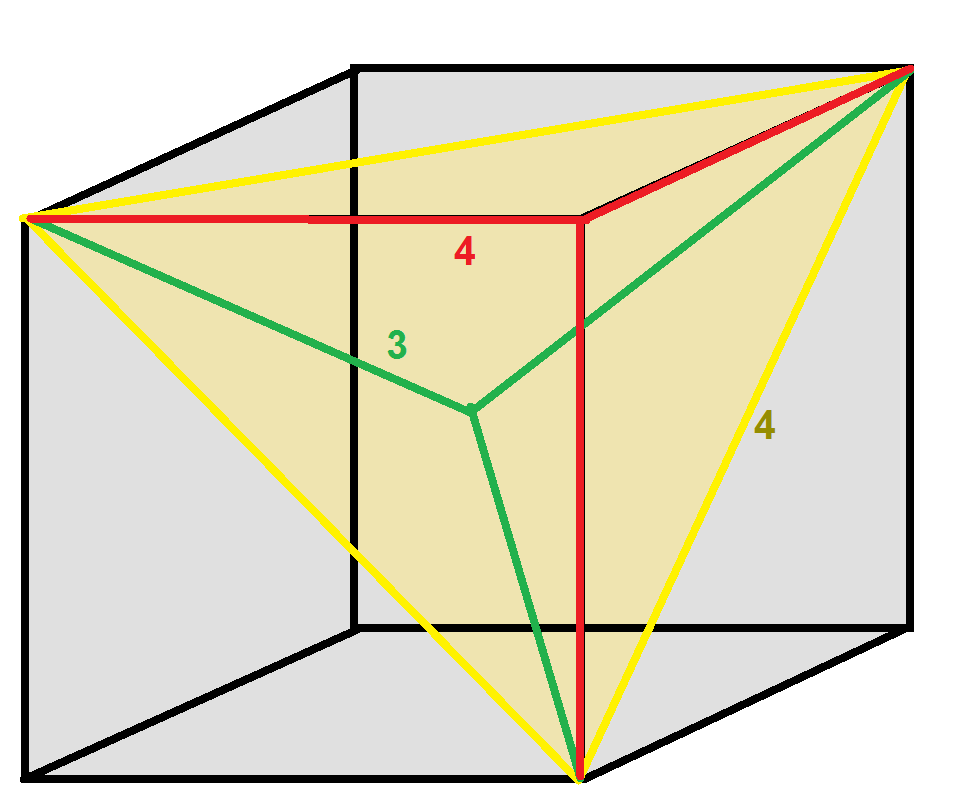
Cartesian coordinates

For an ''alternated cubic honeycomb'', with edges parallel to the axes and with an edge length of 1, the

Cartesian coordinates A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in t ...

of the vertices are: (For all integral values: ''i'',''j'',''k'' with ''i''+''j''+''k''

even Even may refer to: General * Even (given name), a Norwegian male personal name * Even (surname) * Even (people), an ethnic group from Siberia and Russian Far East ** Even language, a language spoken by the Evens * Odd and Even, a solitaire game w ...

) :(i, j, k)

Symmetry

There are two reflective constructions and many alternated

ones; examples:

Alternated cubic honeycomb slices

The ''alternated cubic honeycomb'' can be sliced into sections, where new square faces are created from inside of the octahedron. Each slice will contain up and downward facing

square pyramid In geometry, a square pyramid is a pyramid having a square base. If the apex is perpendicularly above the center of the square, it is a right square pyramid, and has symmetry. If all edge lengths are equal, it is an equilateral square pyramid, ...

s and

sitting on their edges. A second slice direction needs no new faces and includes alternating tetrahedral and octahedral. This slab honeycomb is a

scaliform honeycomb In geometry, a uniform 4-polytope (or uniform polychoron) is a 4-dimensional polytope which is vertex-transitive and whose cells are uniform polyhedra, and faces are regular polygons. There are 47 non-prismatic convex uniform 4-polytopes. There ...

rather than uniform because it has nonuniform cells.

Projection by folding

The ''alternated cubic honeycomb'' can be orthogonally projected into the planar

square tiling In geometry, the square tiling, square tessellation or square grid is a regular tiling of the Euclidean plane. It has Schläfli symbol of meaning it has 4 squares around every vertex. Conway called it a quadrille. The internal angle of the s ...

by a geometric folding operation that maps one pairs of mirrors into each other. The projection of the ''alternated cubic honeycomb'' creates two offset copies of the square tiling

vertex arrangement In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes. For example, a ''square vertex arrangement'' is understood to mean four points in a plane, equ ...

of the plane:

A3/D3 lattice

Its

represents an A₃ lattice or ''D₃ lattice''. This lattice is known as the

face-centered cubic lattice In crystallography, the cubic (or isometric) crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals. There are three main varieties o ...

in crystallography and is also referred to as the cubic close packed lattice as its vertices are the centers of a close-packing with equal spheres that achieves the highest possible average density. The tetrahedral-octahedral honeycomb is the 3-dimensional case of a

. Its Voronoi cell is a

rhombic dodecahedron In geometry, the rhombic dodecahedron is a convex polyhedron with 12 congruent rhombic faces. It has 24 edges, and 14 vertices of 2 types. It is a Catalan solid, and the dual polyhedron of the cuboctahedron. Properties The rhombic dodecahedro ...

, the dual of the

cuboctahedron A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it ...

vertex figure for the tet-oct honeycomb. The D packing can be constructed by the union of two D₃ (or A₃) lattices. The D packing is only a lattice for even dimensions. The kissing number is 2²=4, (2^n-1 for n<8, 240 for n=8, and 2n(n-1) for n>8). : ∪ The A or D lattice (also called A or D) can be constructed by the union of all four A₃ lattices, and is identical to the

of the

disphenoid tetrahedral honeycomb The tetragonal disphenoid tetrahedral honeycomb is a space-filling tessellation (or honeycomb) in Euclidean 3-space made up of identical tetragonal disphenoidal cells. Cells are face-transitive with 4 identical isosceles triangle faces. John Horton ...

, dual honeycomb of the uniform

bitruncated cubic honeycomb The bitruncated cubic honeycomb is a space-filling tessellation (or honeycomb) in Euclidean 3-space made up of truncated octahedra (or, equivalently, bitruncated cubes). It has 4 truncated octahedra around each vertex. Being composed entirely of ...

: It is also the

body centered cubic In crystallography, the cubic (or isometric) crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals. There are three main varieties o ...

, the union of two

s in dual positions. : ∪ ∪ ∪ = dual of = ∪ . The

kissing number In geometry, the kissing number of a mathematical space is defined as the greatest number of non-overlapping unit spheres that can be arranged in that space such that they each touch a common unit sphere. For a given sphere packing (arrangement of ...

of the D lattice is 8 and its

Voronoi tessellation Voronoi or Voronoy is a Slavic masculine surname; its feminine counterpart is Voronaya. It may refer to *Georgy Voronoy (1868–1908), Russian and Ukrainian mathematician **Voronoi diagram **Weighted Voronoi diagram ** Voronoi deformation density ** ...

is a

, , containing all truncated octahedral

Voronoi cell In mathematics, a Voronoi diagram is a partition of a plane into regions close to each of a given set of objects. In the simplest case, these objects are just finitely many points in the plane (called seeds, sites, or generators). For each seed t ...

s, .

Related honeycombs

C3 honeycombs

The ,3,4 ,

Coxeter group In mathematics, a Coxeter group, named after H. S. M. Coxeter, is an abstract group that admits a formal description in terms of reflections (or kaleidoscopic mirrors). Indeed, the finite Coxeter groups are precisely the finite Euclidean refl ...

generates 15 permutations of uniform honeycombs, 9 with distinct geometry including the alternated cubic honeycomb. The expanded cubic honeycomb (also known as the runcinated tesseractic honeycomb) is geometrically identical to the cubic honeycomb.

B3 honeycombs

The ,3^1,1 ,

generates 9 permutations of uniform honeycombs, 4 with distinct geometry including the alternated cubic honeycomb.

A3 honeycombs

This honeycomb is one of five distinct uniform honeycombs
6-1 cases, skipping one with zero marks constructed by the

_3

. The symmetry can be multiplied by the symmetry of rings in the

Coxeter–Dynkin diagram In geometry, a Coxeter–Dynkin diagram (or Coxeter diagram, Coxeter graph) is a graph with numerically labeled edges (called branches) representing the spatial relations between a collection of mirrors (or reflecting hyperplanes). It describe ...

Quasiregular honeycombs

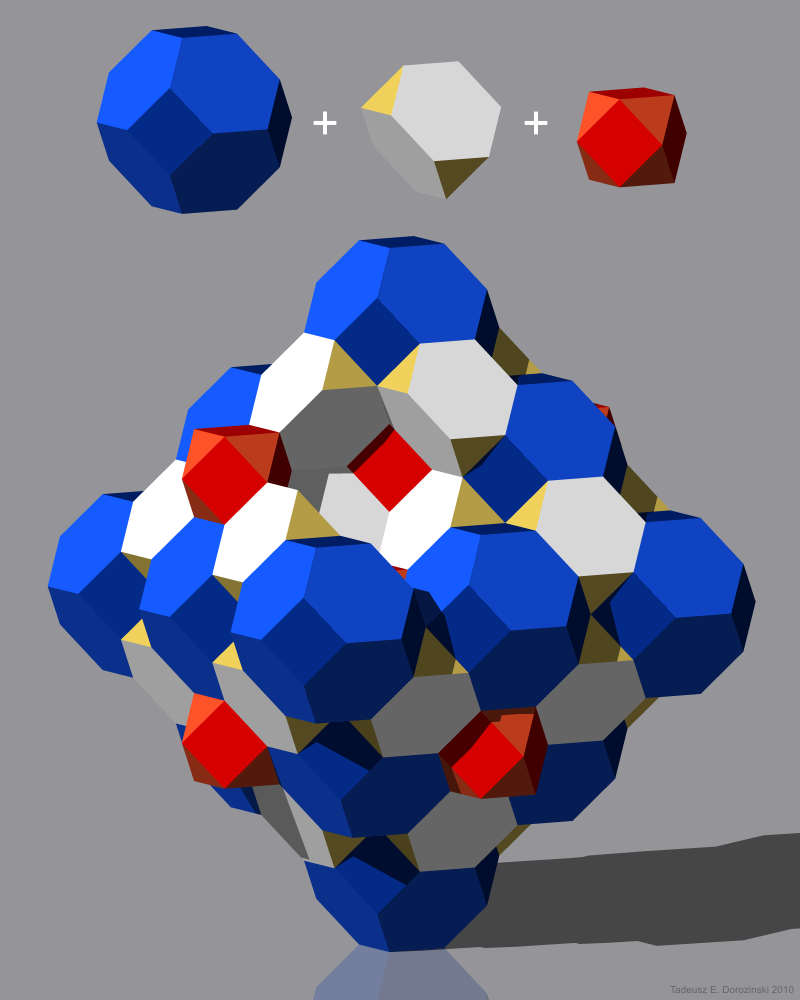
Cantic cubic honeycomb

The cantic cubic honeycomb, cantic cubic cellulation or truncated half cubic honeycomb is a uniform space-filling

(or

) in Euclidean 3-space. It is composed of

truncated octahedra In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces (8 regular hexagon, hexagons and 6 Squa ...

cuboctahedra A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertex (geometry), vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edge (geometry), edges, each separating a t ...

and

truncated tetrahedra In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 equilateral triangle faces, 12 vertices and 18 edges (of two types). It can be constructed by truncating all 4 vertices of a regular tetrahedron ...

in a ratio of 1:1:2. Its

vertex figure In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off. Definitions Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connect ...

is a rectangular

pyramid A pyramid (from el, πυραμίς ') is a structure whose outer surfaces are triangular and converge to a single step at the top, making the shape roughly a pyramid in the geometric sense. The base of a pyramid can be trilateral, quadrilat ...

calls this honeycomb a truncated tetraoctahedrille, and its dual

half oblate octahedrille The rhombic dodecahedral honeycomb (also dodecahedrille) is a space-filling tessellation (or honeycomb (geometry), honeycomb) in Euclidean 3-space. It is the Voronoi diagram of the face-centered cubic sphere-packing, which has the densest possi ...

. :

Symmetry

It has two different uniform constructions. The

_3

construction can be seen with alternately colored

Related honeycombs

It is related to the cantellated cubic honeycomb. Rhombicuboctahedra are reduced to truncated octahedra, and cubes are reduced to truncated tetrahedra.

Runcic cubic honeycomb

The runcic cubic honeycomb or runcic cubic cellulation is a uniform space-filling

(or

) in Euclidean 3-space. It is composed of rhombicuboctahedra,

cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross. The cube is the only r ...

s, and

in a ratio of 1:1:2. Its

is a triangular frustum, with a tetrahedron on one end, cube on the opposite end, and three rhombicuboctahedra around the trapezoidal sides.

calls this honeycomb a 3-RCO-trille, and its dual quarter cubille. : HC A5-P2-P1

Quarter cubille

The dual of a ''runcic cubic honeycomb'' is called a quarter cubille, with

Coxeter diagram Harold Scott MacDonald "Donald" Coxeter, (9 February 1907 – 31 March 2003) was a British and later also Canadian geometer. He is regarded as one of the greatest geometers of the 20th century. Biography Coxeter was born in Kensington to ...

, with faces in 2 of 4 hyperplanes of the

_4

, ,3^1,1symmetry fundamental domain. Cells can be seen as 1/4 of

dissected Dissection (from Latin ' "to cut to pieces"; also called anatomization) is the dismembering of the body of a deceased animal or plant to study its anatomical structure. Autopsy is used in pathology and forensic medicine to determine the cause ...

cube, using 4 vertices and the center. Four cells exist around 6 edges, and 3 cells around 3 edges. : Quarter cubille cell

Related honeycombs

It is related to the

runcinated cubic honeycomb The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation (or honeycomb) in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a re ...

, with quarter of the cubes alternated into tetrahedra, and half expanded into rhombicuboctahedra. This honeycomb can be divided on

truncated square tiling In geometry, the truncated square tiling is a semiregular tiling, semiregular tiling by regular polygons of the Euclidean plane with one square (geometry), square and two octagons on each vertex (geometry), vertex. This is the only edge-to-edge ti ...

planes, using the

octagons In geometry, an octagon (from the Greek ὀκτάγωνον ''oktágōnon'', "eight angles") is an eight-sided polygon or 8-gon. A '' regular octagon'' has Schläfli symbol and can also be constructed as a quasiregular truncated square, t, whi ...

centers of the rhombicuboctahedra, creating

square cupola In geometry, the square cupola, sometimes called lesser dome, is one of the Johnson solids (). It can be obtained as a slice of the rhombicuboctahedron. As in all cupolae, the base polygon has twice as many edges and vertices as the top; in t ...

e. This

is represented by Coxeter diagram , and symbol s₃, with

coxeter notation In geometry, Coxeter notation (also Coxeter symbol) is a system of classifying symmetry groups, describing the angles between fundamental reflections of a Coxeter group in a bracketed notation expressing the structure of a Coxeter-Dynkin diagram ...

symmetry ⁺,4,4 : Runcic_snub_244_honeycomb

Runcicantic cubic honeycomb

The runcicantic cubic honeycomb or runcicantic cubic cellulation is a uniform space-filling

(or

) in Euclidean 3-space. It is composed of truncated cuboctahedra,

truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces (6 octagonal and 8 triangular), 36 edges, and 24 vertices. If the truncated cube has unit edge length, its dual triakis octahedron has edg ...

s and

in a ratio of 1:1:2, with a

mirrored sphenoid In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the o ...

. It is related to the runcicantellated cubic honeycomb.

calls this honeycomb a f-tCO-trille, and its dual

half pyramidille The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation (or honeycomb (geometry), honeycomb) in Euclidean 3-space. It is composed of alternating regular octahedron, octahedra and tetrahedron, ...

. :

Half pyramidille

The dual to the ''runcitruncated cubic honeycomb'' is called a half pyramidille, with

. Faces exist in 3 of 4 hyperplanes of the ,3^1,1

_3

Coxeter group. Cells are irregular pyramids and can be seen as 1/12 of a

, or 1/24 of a

, each defined with three corner and the cube center. : Half pyramidille cell

Related skew apeirohedra

A related uniform

skew apeirohedron In geometry, a skew apeirohedron is an infinite skew polyhedron consisting of nonplanar faces or nonplanar vertex figures, allowing the figure to extend indefinitely without folding round to form a closed surface. Skew apeirohedra have also been ...

exists with the same

, but triangles and square removed. It can be seen as truncated tetrahedra and truncated cubes augmented together. : Runcicantic_cubic_honeycomb_apeirohedron_6688

Runcicantic_cubic_honeycomb_apeirohedron_6688

Related honeycombs

Gyrated tetrahedral-octahedral honeycomb

The gyrated tetrahedral-octahedral honeycomb or gyrated alternated cubic honeycomb is a space-filling

(or

) in

made up of

and

in a ratio of 1:2. It is

vertex-uniform In geometry, a polytope (e.g. a polygon or polyhedron) or a tiling is isogonal or vertex-transitive if all its vertices are equivalent under the symmetries of the figure. This implies that each vertex is surrounded by the same kinds of face in ...

with 8 tetrahedra and 6 octahedra around each vertex. It is not edge-uniform. All edges have 2 tetrahedra and 2 octahedra, but some are alternating, and some are paired. : Gyrated alternated cubic honeycomb

It can be seen as reflective layers of this layer honeycomb:

Construction by gyration

This is a less symmetric version of another honeycomb, tetrahedral-octahedral honeycomb, in which each edge is surrounded by alternating tetrahedra and octahedra. Both can be considered as consisting of layers one cell thick, within which the two kinds of cell strictly alternate. Because the faces on the planes separating these layers form a regular pattern of triangles, adjacent layers can be placed so that each octahedron in one layer meets a tetrahedron in the next layer, or so that each cell meets a cell of its own kind (the layer boundary thus becomes a

reflection Reflection or reflexion may refer to: Science and technology * Reflection (physics), a common wave phenomenon ** Specular reflection, reflection from a smooth surface *** Mirror image, a reflection in a mirror or in water ** Signal reflection, in ...

plane). The latter form is called ''gyrated''. The vertex figure is called a

triangular orthobicupola In geometry, the triangular orthobicupola is one of the Johnson solids (). As the name suggests, it can be constructed by attaching two triangular cupolas () along their bases. It has an equal number of squares and triangles at each vertex; howev ...

, compared to the tetrahedral-octahedral honeycomb whose vertex figure

in a lower symmetry is called a ''triangular gyrobicupola'', so the gyro- prefix is reversed in usage.

Construction by alternation

The geometry can also be constructed with an alternation operation applied to a

hexagonal prismatic honeycomb The triangular prismatic honeycomb or triangular prismatic cellulation is a space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed entirely of triangular prisms. It is constructed from a triangular tiling extruded into pri ...

. The

hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. Prisms are polyhedrons; this polyhedron has 8 faces, 18 edges, and 12 vertices.. Since it has 8 faces, it is an octahedron. However, the term ''octahedron'' is primarily used to ...

cells become

and the voids create

triangular bipyramid In geometry, the triangular bipyramid (or dipyramid) is a type of hexahedron, being the first in the infinite set of face-transitive bipyramids. It is the dual of the triangular prism with 6 isosceles triangle faces. As the name suggests, i ...

s which can be divided into pairs of

of this honeycomb. This honeycomb with bipyramids is called a ditetrahedral-octahedral honeycomb. There are 3 Coxeter-Dynkin diagrams, which can be seen as 1, 2, or 3 colors of octahedra: # # #

Gyroelongated alternated cubic honeycomb

The gyroelongated alternated cubic honeycomb or elongated triangular antiprismatic cellulation is a space-filling

(or

) in

. It is composed of

triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides. A right triangular prism has rectangular sides, otherwise it is ''oblique''. A unif ...

s, and

in a ratio of 1:2:2. It is vertex-transitive with 3 octahedra, 4 tetrahedra, 6 triangular prisms around each vertex. It is one of 28

convex uniform honeycomb In geometry, a convex uniform honeycomb is a uniform polytope, uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex polyhedron, convex uniform polyhedron, uniform polyhedral cells. Twenty-eight such honey ...

s. The

elongated alternated cubic honeycomb The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation (or honeycomb (geometry), honeycomb) in Euclidean 3-space. It is composed of alternating regular octahedron, octahedra and tetrahedron, ...

has the same arrangement of cells at each vertex, but the overall arrangement differs. In the ''elongated'' form, each prism meets a tetrahedron at one of its triangular faces and an octahedron at the other; in the ''gyroelongated'' form, the prism meets the same kind of

deltahedron In geometry, a deltahedron (plural ''deltahedra'') is a polyhedron whose face (geometry), faces are all equilateral triangles. The name is taken from the Greek language, Greek upper case delta (letter), delta (Δ), which has the shape of an equ ...

at each end. :

Elongated alternated cubic honeycomb

The elongated alternated cubic honeycomb or elongated triangular gyroprismatic cellulation is a space-filling

(or

) in

. It is composed of

s, and

in a ratio of 1:2:2. It is vertex-transitive with 3 octahedra, 4 tetrahedra, 6 triangular prisms around each vertex. Each prism meets an octahedron at one end and a tetrahedron at the other. It is one of 28

s. It has a ''gyrated'' form called the

gyroelongated alternated cubic honeycomb The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of alternating regular octahedra and tetrahedra in a ratio of 1:2. Other names incl ...

with the same arrangement of cells at each vertex. :

Notes

References

John H. Conway John Horton Conway (26 December 1937 – 11 April 2020) was an English people, English mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory. He also made contributions to ...

, Heidi Burgiel,

Chaim Goodman-Strauss Chaim Goodman-Strauss (born June 22, 1967 in Austin TX) is an American mathematician who works in convex geometry, especially aperiodic tiling. He is on the faculty of the University of Arkansas and is a co-author with John H. Conway of ''The Sym ...

, (2008) ''The Symmetries of Things'', (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, Architectonic and Catoptric tessellations, p 292–298, includes all the nonprismatic forms) * George Olshevsky, ''Uniform Panoploid Tetracombs'', Manuscript (2006) ''(Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)'' *

Branko Grünbaum Branko Grünbaum ( he, ברנקו גרונבאום; 2 October 1929 – 14 September 2018) was a Croatian-born mathematician of Jewish descentGeombinatorics Alexander Soifer is a Russian-born American mathematician and mathematics author. His works include over 400 articles and 13 books. Soifer obtained his Ph.D. in 1973 and has been a professor of mathematics at the University of Colorado since 197 ...

4(1994), 49 - 56. * Norman Johnson ''Uniform Polytopes'', Manuscript (1991) * * * Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995,

** (Paper 22) H.S.M. Coxeter, ''Regular and Semi Regular Polytopes I'', ath. Zeit. 46 (1940) 380–407, MR 2,10(1.9 Uniform space-fillings) ** (Paper 24) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes III'', ath. Zeit. 200 (1988) 3-45* A. Andreini, ''Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative'' (On the regular and semiregular nets of polyhedra and on the corresponding correlative nets), Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129. * D. M. Y. Sommerville, ''An Introduction to the Geometry of n Dimensions.'' New York, E. P. Dutton, 1930. 196 pp. (Dover Publications edition, 1958) Chapter X: The Regular Polytopes *

External links

Architectural design made with Tetrahedrons and regular Pyramids based square.(2003)
*

{{Honeycombs Honeycombs (geometry) 4-polytopes

Cartesian coordinates

Symmetry

Alternated cubic honeycomb slices

Projection by folding

A3/D3 lattice

Related honeycombs

C3 honeycombs

B3 honeycombs

A3 honeycombs

Quasiregular honeycombs

Cantic cubic honeycomb

Symmetry

Related honeycombs

Runcic cubic honeycomb

Quarter cubille

Related honeycombs

Runcicantic cubic honeycomb

Half pyramidille

Related skew apeirohedra

Related honeycombs

Gyrated tetrahedral-octahedral honeycomb

Construction by gyration

Construction by alternation

Gyroelongated alternated cubic honeycomb

Elongated alternated cubic honeycomb

See also

Notes

References

External links