Berkson's Paradox on:
[Wikipedia]
[Google]
[Amazon]
 Berkson's paradox, also known as Berkson's bias,
Berkson's paradox, also known as Berkson's bias,
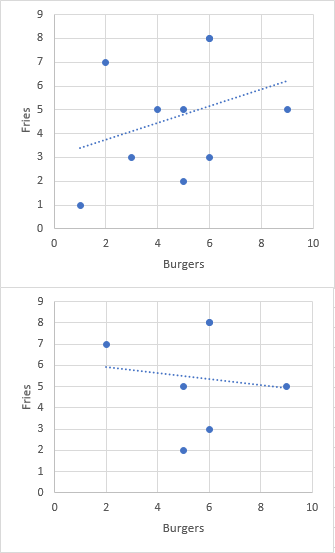 The most common example of Berkson's paradox is a false observation of a ''negative'' correlation between two desirable traits, i.e., that members of a population which have some desirable trait tend to lack a second. Berkson's paradox occurs when this observation appears true when in reality the two properties are unrelated—or even ''positively'' correlated—because members of the population where both are absent are not equally observed. For example, a person may observe from their experience that fast food restaurants in their area which serve good hamburgers tend to serve bad fries and vice versa; but because they would likely not eat anywhere where ''both'' were bad, they fail to allow for the large number of restaurants in this category which would weaken or even flip the correlation.
The most common example of Berkson's paradox is a false observation of a ''negative'' correlation between two desirable traits, i.e., that members of a population which have some desirable trait tend to lack a second. Berkson's paradox occurs when this observation appears true when in reality the two properties are unrelated—or even ''positively'' correlated—because members of the population where both are absent are not equally observed. For example, a person may observe from their experience that fast food restaurants in their area which serve good hamburgers tend to serve bad fries and vice versa; but because they would likely not eat anywhere where ''both'' were bad, they fail to allow for the large number of restaurants in this category which would weaken or even flip the correlation.
Why are handsome men such jerks?
Numberphile: Does Hollywood ruin books?
– An education video on Berkson's paradox in popular culture Probability theory paradoxes Statistical paradoxes Medical statistics
collider
A collider is a type of particle accelerator which brings two opposing particle beams together such that the particles collide. Colliders may either be ring accelerators or linear accelerators.
Colliders are used as a research tool in particle ...
bias, or Berkson's fallacy, is a result in conditional probability
In probability theory, conditional probability is a measure of the probability of an event occurring, given that another event (by assumption, presumption, assertion or evidence) has already occurred. This particular method relies on event B occur ...
and statistics
Statistics (from German language, German: ''wikt:Statistik#German, Statistik'', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of ...
which is often found to be counterintuitive
A paradox is a logically self-contradictory statement or a statement that runs contrary to one's expectation. It is a statement that, despite apparently valid reasoning from true premises, leads to a seemingly self-contradictory or a logically u ...
, and hence a veridical paradox
A paradox is a logically self-contradictory statement or a statement that runs contrary to one's expectation. It is a statement that, despite apparently valid reasoning from true premises, leads to a seemingly self-contradictory or a logically u ...
. It is a complicating factor arising in statistical tests of proportions. Specifically, it arises when there is an ascertainment bias
In statistics, sampling bias is a bias in which a sample is collected in such a way that some members of the intended population have a lower or higher sampling probability than others. It results in a biased sample of a population (or non-human f ...
inherent in a study design. The effect is related to the explaining away phenomenon in Bayesian network
A Bayesian network (also known as a Bayes network, Bayes net, belief network, or decision network) is a probabilistic graphical model that represents a set of variables and their conditional dependencies via a directed acyclic graph (DAG). Bay ...
s, and conditioning on a collider in graphical model
A graphical model or probabilistic graphical model (PGM) or structured probabilistic model is a probabilistic model for which a Graph (discrete mathematics), graph expresses the conditional dependence structure between random variables. They are ...
s.
It is often described in the fields of medical statistics
Medical statistics deals with applications of statistics to medicine and the health sciences, including epidemiology, public health, forensic medicine, and clinical research. Medical statistics has been a recognized branch of statistics in the U ...
or biostatistics
Biostatistics (also known as biometry) are the development and application of statistical methods to a wide range of topics in biology. It encompasses the design of biological experiments, the collection and analysis of data from those experime ...
, as in the original description of the problem by Joseph Berkson
Joseph Berkson (14 May 1899 – 12 September 1982) was trained as a physicist (BSc 1920 College of City of New York, M.A., 1922, Columbia), physician (M.D., 1927, Johns Hopkins), and statistician (Dr.Sc., 1928, Johns Hopkins).O'Fallon WM (1998). " ...
.
Examples
Overview
 The most common example of Berkson's paradox is a false observation of a ''negative'' correlation between two desirable traits, i.e., that members of a population which have some desirable trait tend to lack a second. Berkson's paradox occurs when this observation appears true when in reality the two properties are unrelated—or even ''positively'' correlated—because members of the population where both are absent are not equally observed. For example, a person may observe from their experience that fast food restaurants in their area which serve good hamburgers tend to serve bad fries and vice versa; but because they would likely not eat anywhere where ''both'' were bad, they fail to allow for the large number of restaurants in this category which would weaken or even flip the correlation.
The most common example of Berkson's paradox is a false observation of a ''negative'' correlation between two desirable traits, i.e., that members of a population which have some desirable trait tend to lack a second. Berkson's paradox occurs when this observation appears true when in reality the two properties are unrelated—or even ''positively'' correlated—because members of the population where both are absent are not equally observed. For example, a person may observe from their experience that fast food restaurants in their area which serve good hamburgers tend to serve bad fries and vice versa; but because they would likely not eat anywhere where ''both'' were bad, they fail to allow for the large number of restaurants in this category which would weaken or even flip the correlation.
Original illustration
Berkson's original illustration involves a retrospective study examining arisk factor
In epidemiology, a risk factor or determinant is a variable associated with an increased risk of disease or infection.
Due to a lack of harmonization across disciplines, determinant, in its more widely accepted scientific meaning, is often use ...
for a disease in a statistical sample from a hospital
A hospital is a health care institution providing patient treatment with specialized health science and auxiliary healthcare staff and medical equipment. The best-known type of hospital is the general hospital, which typically has an emerge ...
in-patient population. Because samples are taken from a hospital in-patient population, rather than from the general public, this can result in a spurious negative association between the disease and the risk factor. For example, if the risk factor is diabetes and the disease is cholecystitis
Cholecystitis is inflammation of the gallbladder. Symptoms include right upper abdominal pain, pain in the right shoulder, nausea, vomiting, and occasionally fever. Often gallbladder attacks (biliary colic) precede acute cholecystitis. The pain l ...
, a hospital patient ''without'' diabetes is ''more'' likely to have cholecystitis than a member of the general population, since the patient must have had some non-diabetes (possibly cholecystitis-causing) reason to enter the hospital in the first place. That result will be obtained regardless of whether there is any association between diabetes and cholecystitis in the general population.Ellenberg example
An example presented byJordan Ellenberg
Jordan Stuart Ellenberg (born October 30, 1971) is an American mathematician who is a professor of mathematics at the University of Wisconsin–Madison. His research involves arithmetic geometry. He is also an author of both fiction and non-ficti ...
: Suppose Alex will only date a man if his niceness plus his handsomeness exceeds some threshold. Then nicer men do not have to be as handsome to qualify for Alex's dating pool. So, ''among the men that Alex dates'', Alex may observe that the nicer ones are less handsome on average (and vice versa), even if these traits are uncorrelated in the general population. Note that this does not mean that men in the dating pool compare unfavorably with men in the population. On the contrary, Alex's selection criterion means that Alex has high standards. The average nice man that Alex dates is actually more handsome than the average man in the population (since even among nice men, the ugliest portion of the population is skipped). Berkson's negative correlation is an effect that arises ''within'' the dating pool: the rude men that Alex dates must have been ''even more'' handsome to qualify.Quantitative example
As a quantitative example, suppose a collector has 1000postage stamp
A postage stamp is a small piece of paper issued by a post office, postal administration, or other authorized vendors to customers who pay postage (the cost involved in moving, insuring, or registering mail), who then affix the stamp to the fa ...
s, of which 300 are pretty and 100 are rare, with 30 being both pretty and rare. 30% of all his stamps are pretty and 10% of his pretty stamps are rare, so prettiness tells nothing about rarity. He puts the 370 stamps which are pretty or rare on display. Just over 27% of the stamps on display are rare (100/370), but still only 10% of the pretty stamps are rare (and 100% of the 70 not-pretty stamps on display are rare). If an observer only considers stamps on display, they will observe a spurious negative relationship between prettiness and rarity as a result of the selection bias
Selection bias is the bias introduced by the selection of individuals, groups, or data for analysis in such a way that proper randomization is not achieved, thereby failing to ensure that the sample obtained is representative of the population int ...
(that is, not-prettiness strongly indicates rarity in the display, but not in the total collection).
Statement
Twoindependent
Independent or Independents may refer to:
Arts, entertainment, and media Artist groups
* Independents (artist group), a group of modernist painters based in the New Hope, Pennsylvania, area of the United States during the early 1930s
* Independ ...
events become conditionally dependent given that at least one of them occurs. Symbolically:
:If , , and , then and hence .
:* Event and event may or may not occur
:
:* , a conditional probability
In probability theory, conditional probability is a measure of the probability of an event occurring, given that another event (by assumption, presumption, assertion or evidence) has already occurred. This particular method relies on event B occur ...
, is the probability of observing event given that is true.
:* Explanation: Event and are independent of each other
:
:
:* is the probability of observing event given that ''and'' ( ''or'' ) occurs. This can also be written as
:* Explanation: The probability of given both ''and'' ( ''or'' ) is smaller than the probability of given ( ''or'' )
:
In other words, given two independent events, if you consider only outcomes where at least one occurs, then they become conditionally dependent, as shown above.
Explanation
The cause is that the ''conditional'' probability of event '''' occurring, ''given'' that it or occurs, is inflated: it is higher than the ''unconditional'' probability, because we have ''excluded'' cases where ''neither'' occur. : :conditional probability inflated relative to unconditional One can see this in tabular form as follows: the yellow regions are the outcomes where at least one event occurs (and ~A means "not A"). For instance, if one has a sample of , and both '''' and occur independently half the time ( ), one obtains: So in outcomes, either '''' or occurs, of which have '''' occurring. By comparing the conditional probability of '''' to the unconditional probability of '''': : We see that the probability of is higher () in the subset of outcomes where ('''' ''or'' '''') occurs, than in the overall population (). On the other hand, the probability of given both and ('''' or '''') is simply the unconditional probability of '''', , since '''' is independent of ''''. In the numerical example, we have conditioned on being in the top row: Here the probability of '''' is . Berkson's paradox arises because the conditional probability of '''' given ''within the three-cell subset'' equals the conditional probability in the overall population, but the unconditional probability within the subset is inflated relative to the unconditional probability in the overall population, hence, within the subset, the presence of decreases the conditional probability of '''' (back to its overall unconditional probability): : :See also
*Simpson's paradox
Simpson's paradox is a phenomenon in probability and statistics in which a trend appears in several groups of data but disappears or reverses when the groups are combined. This result is often encountered in social-science and medical-science st ...
* Survivorship bias
Survivorship bias or survival bias is the logical error of concentrating on entities that passed a selection process while overlooking those that did not. This can lead to incorrect conclusions because of incomplete data.
Survivorship bias is ...
References
* {{cite journal , last=Berkson , first=Joseph , date=June 1946 , title=Limitations of the Application of Fourfold Table Analysis to Hospital Data , journal= Biometrics Bulletin , volume=2 , issue=3 , pages=47–53 , doi=10.2307/3002000 , jstor=3002000 , pmid=21001024 (The paper is frequently miscited as Berkson, J. (1949) Biological Bulletin 2, 47–53.) * Jordan Ellenberg,Why are handsome men such jerks?
External links
Numberphile: Does Hollywood ruin books?
– An education video on Berkson's paradox in popular culture Probability theory paradoxes Statistical paradoxes Medical statistics